思考するAI「Qwen3-Max-Thinking」誕生!数学×コードで覚醒する新モデルの実力とは

- 数学推論とコード実行を組み合わせることで段階的推論を実現
- Test-Time Computeにより、タスクの難易度に応じて内部計算量を動的に増減
- APIではOpenAI互換の形式で利用でき、数学・コード修正・データ処理など幅広いタスクで高い性能を示す
2025年9月、AlibabaはQwen3-Maxシリーズにおいて、推論性能を極限まで高めたモデル「Qwen3-Max-Thinking」を発表。
さらに2025年11月に初期プレビューを発表しました。本発表で推論ベンチマーク100%を達成しており、性能の高さが伺えます。
本記事ではQwen3-Max-Thinkingの概要から仕組み、実際の使い方をお伝えします。最後までお読みいただくことでQwen3-Max-Thinkingの理解が深まり、実際にAPI経由で使えるようになります。
ぜひ最後までお読みください!
\生成AIを活用して業務プロセスを自動化/
Qwen3-Max-Thinkingの概要
Qwen3-Max-Thinkingは、すでに登場していたQwen3-Max-Instructをベースに、論理的思考や数学的推論を中心に強化したモデルであり、「考えることに特化したAI」として位置づけられています。
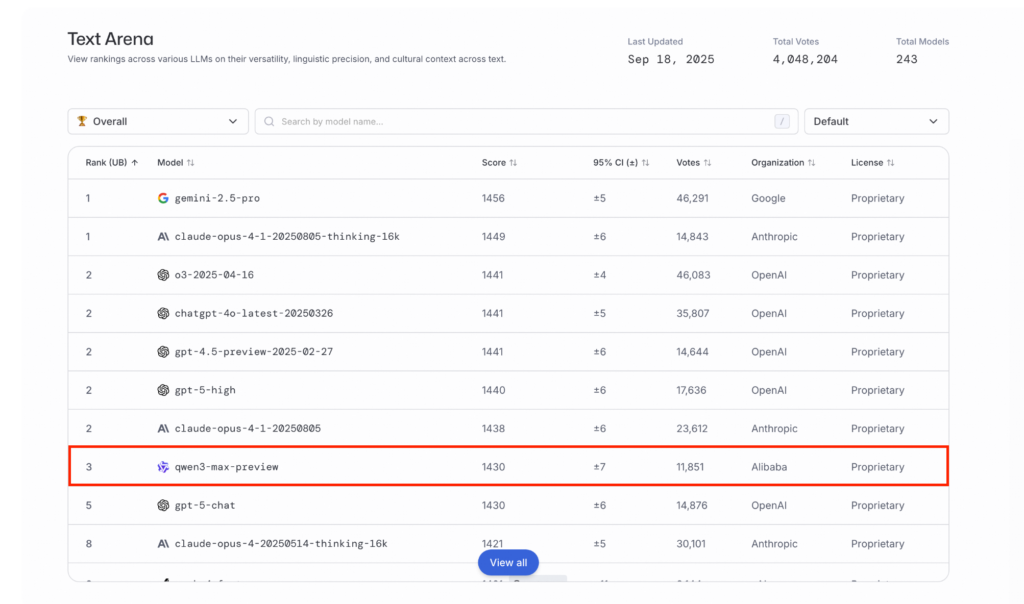
Qwen3-Max-Thinkingは、1兆を超えるパラメータと36兆トークンによる事前学習を経て構築されたQwen3-Maxを共有しつつ、コードインタープリタと推論時計算を統合。
これにより、複雑な問題に直面した際、内部的に演算を拡張しながら最適な答えを導き出すことが可能となりました。
特に注目すべきは、AIME 2025やHMMTといった数学系推論ベンチマークで満点(100%)を達成した点です。
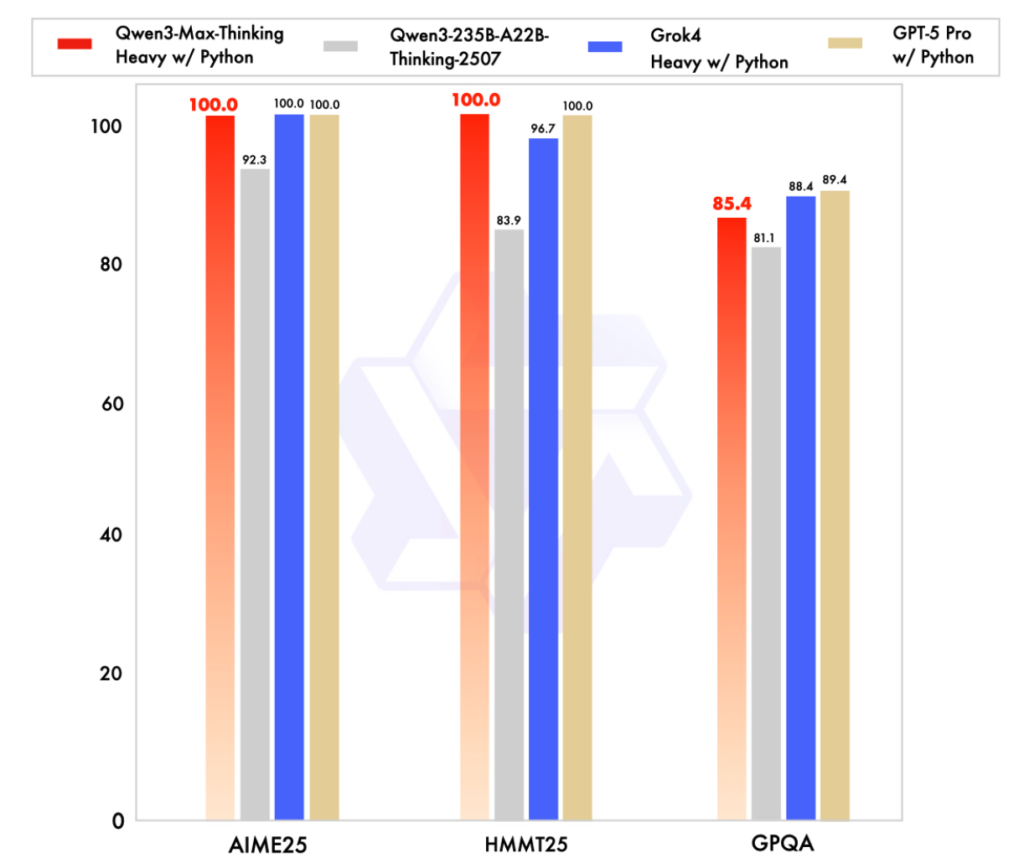
まだトレーニング途中のプレビュー版であるにもかかわらず、高い性能を示していることから、「人間に近い思考能力を持つ初の汎用LLM」として高い関心を集めています。
Qwen3-Max-Thinkingの仕組み
Qwen3-Max-Thinkingは、Qwen3-Maxシリーズの中でも「推論過程を最適化する」ことに特化したモデル構造を採用。
そのベースにあるのが、Mixture of Expertsアーキテクチャと推論時計算の動的制御です。
Mixture of Expertsによる効率的な思考経路
Qwen3-Max-Thinkingは、1兆を超えるパラメータをすべて同時に稼働させるのではなく、入力内容に応じて最も適した専門ブロック(Expert)を選択。
この「選択的推論」により、単一モデルのような一律処理ではなく、課題に応じて異なる思考経路を辿る柔軟性を実現しています。結果として、巨大なモデルでありながらも安定かつ効率的に動作します。
コードインタープリタの統合
Thinkingモデルのもう一つの中核要素は、内部コードインタープリタの組み込みです。
モデル自身がPythonコードを生成・実行し、計算結果をその場で再利用します。
たとえば、数式や統計処理を含む問いに対しては、まずコードで計算を行い、結果を検証したうえで最終回答を生成します。これにより、曖昧な推測ではなく、論理的な裏付けを伴う応答が可能になっています。
Test-Time Compute
通常のLLMは、推論時に固定された計算量で応答を出します。しかしQwen3-Max-Thinkingは、問題の複雑さに応じて計算量を動的に拡張。難易度の高い課題では内部的に複数の思考ルートを展開し、それぞれの出力を比較して最も妥当な結論を採用します。
この仕組みが「Scaled Test-Time Compute」と呼ばれ、AIME 2025などの数学的推論で満点を取る要因です。
Qwen3-Max-Thinkingのアーキテクチャは、単にパラメータを増やす「拡大路線」ではなく、思考の質を高めるための設計に重点を置いています。
Qwen3-Max-Thinkingの特徴
Qwen3-Max-Thinkingは、Qwen3-Maxシリーズの中でも特に推論精度と思考過程の一貫性に優れたモデルです。その特徴は、単なる出力の正確さにとどまらず、どのようにして答えにたどり着くのかという「思考の質」にあります。
並列思考による安定した出力
Thinkingモデルは、内部で複数の推論経路を同時に走らせ、最も信頼性の高い解を選択する仕組みを持ちます。この「並列思考」によって、同じ質問でも安定した応答を再現できるようになりました。
特に、論理問題やプログラミングのバグ修正といったタスクでは、思考のぶれが小さく、一貫性のある出力が得られます。
コード実行との融合
もう一つの大きな特徴が、コードインタープリタとの融合です。
Qwen3-Max-Thinkingは、自然言語による推論の途中でプログラムを実行し、その結果を再度推論材料として取り込むことができます。
これにより、単なる「テキストの予測」ではなく、「実際に考えて確認する」というプロセスが実現されています。
AIが自ら検算や仮説検証を行う姿は、従来のLLMとは明確に異なる進化です。
なお、リアルタイム音声出力も可能な万能AIモデル【Qwen3-Omni】について詳しく知りたい方は、下記の記事を合わせてご確認ください。

Qwen3-Max-Thinkingの安全性・制約
Qwen3-Max-Thinkingは高度な推論能力を備えていますが、その自由度の高さゆえに、入力内容や利用環境によっては安全上のリスクが伴う可能性があります。
Qwen3シリーズには内部ロジックとしての基本的な安全対策が実装されている一方で、企業利用やプロダクション環境では、外部の安全レイヤーと組み合わせて運用することが前提となっています。
リアルタイムの不適切コンテンツ検知
Qwen3Guardは、Alibaba Cloudが公開する外部モデレーションモデルであり、Qwen3-Max-Thinkingを含むあらゆるLLMの「前処理・後処理」での利用を想定。※1
リアルタイムのトークンレベル検知に対応しており、以下のような不適切コンテンツをモニタリングします。
- 個人情報(PII)
- 暴力・ヘイト・アダルト表現
- 攻撃的・有害表現
- 業界ごとのコンプライアンス違反
Thinkingモデルは入力内容に応じて推論が深く分岐するため、Qwen3Guardを前段(プロンプト検査)と後段(出力検査)に挟む構成が推奨されます。
AI Guardrails
AI Guardrailsは、LLMアプリケーションを安全に運用するための統合セーフティレイヤーで、入力・出力の双方を監視してリスクを自動検知します。※2
検知対象は、以下のような攻撃・誘導・規制リスクです。
- プロンプトインジェクション
- 禁止APIの実行誘導
- センシティブ情報の抽出・外部送信
- 法的・規制上のリスクのある生成内容
Thinkingモードでは推論が多段化しやすく、ユーザーの意図しない方向へ話題が誘導される可能性もあるため、AI Guardrailsのような外部安全レイヤーを併用することで、モデル単体ではカバーしきれないリスクを補完できます。
Qwen3-Max-Thinkingの料金
Qwen3-Max-Thinkingは、Alibaba CloudのModel StudioおよびQwen Chat上で提供されています。
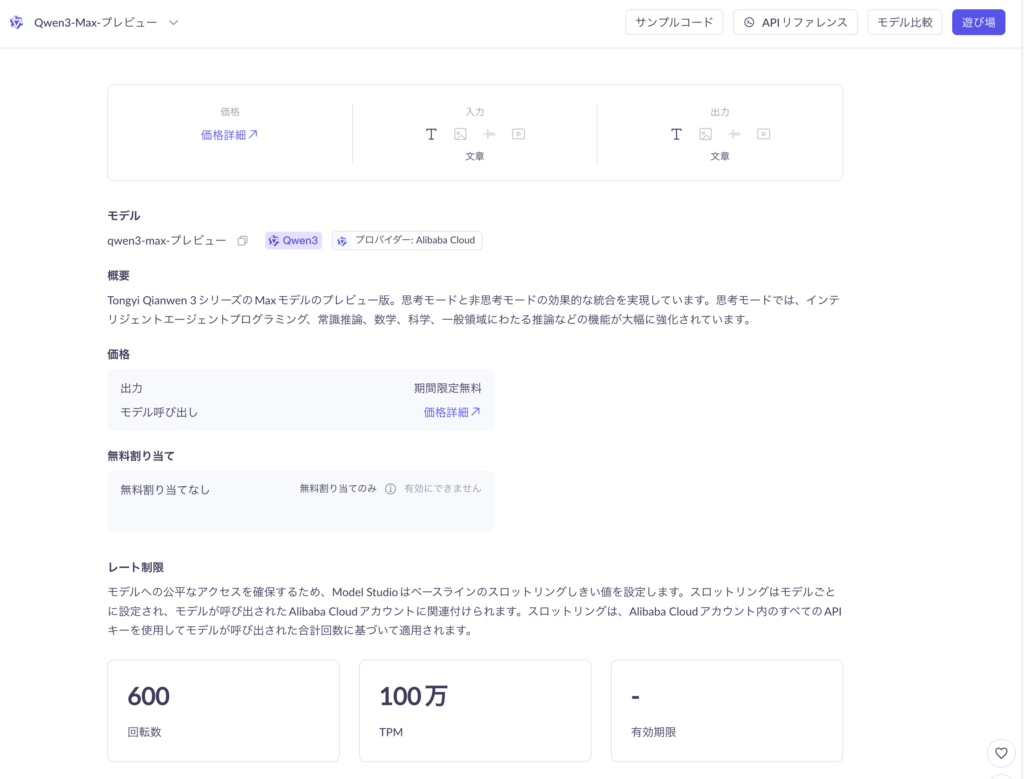
ただし、現時点(2025年11月時点)では「early preview(プレビュー版)」としての提供であり、正式な料金体系はまだ公開されておらず、期間限定無料となっています。※3
Qwen3-Max-Thinkingのライセンス
Qwen3-Max-Thinkingのライセンスは、Alibaba Cloudの利用規約およびQwen Chatのサービス規約に基づいています。現段階ではオープンウェイトとしての公開は行われておらず、API経由でのみ利用可能なクローズドモデルです。
そのため、ローカル環境への直接インストールや独自改変はできません。
| 利用用途 | 可否 |
|---|---|
| 商用利用 | 🔺(現時点ではプレビュー用途のみ) |
| 改変 | ❌ |
| 配布 | ❌ |
| 特許使用 | 明記なし |
| 私的使用 | ⭕️ |
なお、日本語含む10言語対応の多言語音声生成モデル【Qwen3-TTS-Flash】について詳しく知りたい方は、下記の記事を合わせてご確認ください。

Qwen3-Max-Thinkingの実装方法
Qwen3-Max-Thinkingは、Qwen ChatとAlibaba Cloud APIの2通りで利用可能です。
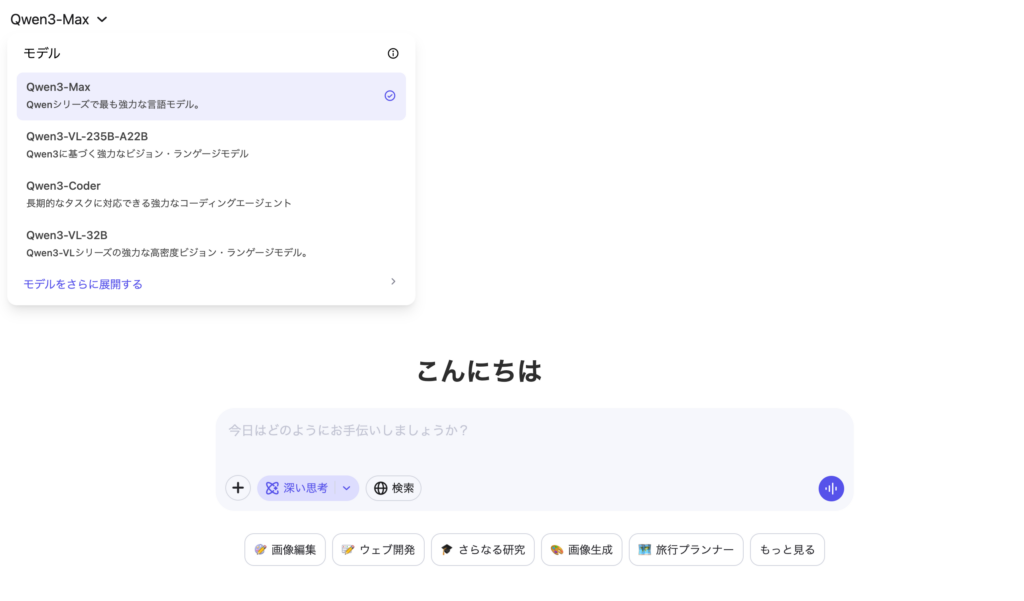
Qwen Chatでは深い思考にチェックを入れるとQwen3-Max-Thinkingを使ってやり取りが可能。
Alibaba Cloud APIで利用する
Alibaba Cloud APIを利用する場合にはモデルをqwen3-max-preview、enable_thinkingをTrueにする必要があります。
サンプルコードはこちら
import requests, json
API_KEY = ""
URL = "https://dashscope-intl.aliyuncs.com/compatible-mode/v1/chat/completions"
payload = {
"model": "qwen3-max-preview",
"stream": False,
"messages": [
{"role":"system","content":"丁寧で論理的に回答してください"},
{"role":"user","content":"AIMEスタイルの整数問題を手順つきで解いて"}
],
"extra_body": {
"enable_thinking": True,
"thinking_budget": 1024,
"enable_code_interpreter": True
}
}
headers = {
"Authorization": f"Bearer {API_KEY}",
"Content-Type": "application/json"
}
r = requests.post(URL, headers=headers, data=json.dumps(payload))
r.raise_for_status()
data = r.json()
print(data["choices"][0]["message"].get("content",""))
# 思考過程(返るときだけ)
rc = data["choices"][0]["message"].get("reasoning_content")
if rc:
print("\n--- reasoning ---\n" + rc)結果はこちら
もちろんです。以下に、**AIME(American Invitational Mathematics Examination)スタイルの整数問題**を1問提示し、それを**丁寧で論理的な手順**で解いていきます。
---
## 【問題】
正の整数 \( n \) であって、\( n^2 + 12n - 2007 \) が完全平方数となるようなものをすべて求め、それらの和を求めよ。
---
## 【解答・解説】
### Step 1:問題の構造を把握する
与えられた式:
\[
n^2 + 12n - 2007 = k^2 \quad \text{(ある整数 } k \text{ に対して)}
\]
つまり、この式が**ある整数の2乗**になるような正の整数 \( n \) を探す問題です。
---
### Step 2:平方完成を行う
左辺を平方完成して、式を整理しましょう。
\[
n^2 + 12n - 2007 = (n+6)^2 - 36 - 2007 = (n+6)^2 - 2043
\]
したがって、
\[
(n+6)^2 - k^2 = 2043
\]
これは**平方の差**なので、因数分解できます:
\[
(n+6 - k)(n+6 + k) = 2043
\]
---
### Step 3:2043を素因数分解する
2043を素因数分解しましょう。
まず、2043 ÷ 3 = 681
681 ÷ 3 = 227
227は素数です(√227 ≈ 15.06 なので、2〜15で割ってみる → 割れない)
よって、
\[
2043 = 3^2 \times 227
\]
---
### Step 4:因数の組み合わせを考える
\[
(n+6 - k)(n+6 + k) = 2043
\]
ここで、\( a = n+6 - k \), \( b = n+6 + k \) とおくと、
- \( a \cdot b = 2043 \)
- \( a < b \) (なぜなら \( k > 0 \) より)
- \( a \) と \( b \) は**同符号**であり、\( n \) が正の整数なので \( n+6 > 0 \)、かつ \( k \geq 0 \) より、\( b = n+6 + k > 0 \)。したがって \( a > 0 \) としてもよい(負の因数ペアは後で検討)
→ まずは**正の因数ペア**のみを考えます。
2043の正の約数を列挙します。
素因数分解:\( 3^2 \times 227 \)
約数の個数:\( (2+1)(1+1) = 6 \)個
具体的には:
1, 3, 9, 227, 681, 2043
これらから、\( a < b \), \( a \cdot b = 2043 \) となるペアを列挙:
- (1, 2043)
- (3, 681)
- (9, 227)
(※ 227×9 は既に含まれているので、これ以上はない)
---
### Step 5:各ペアから \( n \) を求める
各ペア \( (a, b) \) に対して、
\[
a = n+6 - k \\
b = n+6 + k
\]
これらを足すと:
\[
a + b = 2(n+6) \Rightarrow n+6 = \frac{a+b}{2} \Rightarrow n = \frac{a+b}{2} - 6
\]
また、引くと:
\[
b - a = 2k \Rightarrow k = \frac{b-a}{2}
\]
→ \( a+b \) が偶数でないと \( n \) が整数にならない。つまり、**\( a \) と \( b \) の和が偶数**、すなわち**両方奇数 or 両方偶数**が必要。
2043は奇数なので、すべての因数は奇数 → \( a, b \) ともに奇数 → 和は偶数 → OK!
では、各ペアで計算してみましょう。
---
#### ペア①: \( a=1, b=2043 \)
\[
n = \frac{1 + 2043}{2} - 6 = \frac{2044}{2} - 6 = 1022 - 6 = 1016
\]
→ 正の整数。OK。
---
#### ペア②: \( a=3, b=681 \)
\[
n = \frac{3 + 681}{2} - 6 = \frac{684}{2} - 6 = 342 - 6 = 336
\]
→ OK。
---
#### ペア③: \( a=9, b=227 \)
\[
n = \frac{9 + 227}{2} - 6 = \frac{236}{2} - 6 = 118 - 6 = 112
\]
→ OK。
---
### Step 6:負の因数ペアについて考える?
\( a \cdot b = 2043 \) で、\( a < b \) だが両方負の場合も考えられます。
例えば \( (-2043, -1) \) など。
このとき、
\[
n+6 = \frac{a + b}{2}
\]
が負になる可能性があり、\( n \) が正の整数になるか確認が必要です。
試しに \( a = -2043, b = -1 \) で計算:
\[
n = \frac{-2043 + (-1)}{2} - 6 = \frac{-2044}{2} - 6 = -1022 - 6 = -1028
\]
→ 負なので不適。
他の負のペアも同様に \( n \) は負になるため、**除外**します。
---
### Step 7:得られた \( n \) の値をまとめる
上記より、条件を満たす正の整数 \( n \) は:
\[
n = 112,\ 336,\ 1016
\]
---
### Step 8:その和を求める
\[
112 + 336 + 1016 = ?
\]
まず 112 + 336 = 448
448 + 1016 = **1464**
---
## 【最終答え】
\[
\boxed{1464}
\]
---
## 【補足・検算】
一応、どれか1つについて元の式が平方数になるか確認してみましょう。
例:\( n = 112 \)
\[
n^2 + 12n - 2007 = 112^2 + 12 \times 112 - 2007 = 12544 + 1344 - 2007 = 13888 - 2007 = 11881
\]
\( \sqrt{11881} = 109 \)? → \( 109^2 = 11881 \) → ○
他の値も同様に検算可能ですが、構造的に正しいので省略します。
---
## 【まとめ:AIME問題を解く手順】
1. 条件式を「平方数=…」の形にする。
2. 平方完成や変形により、平方の差(または和)の形を作る。
3. 因数分解可能な形に持ち込み、整数解の候補を絞る。
4. 約数を列挙し、条件(正の整数、偶奇、範囲など)でフィルタリング。
5. 各候補から未知数を復元し、条件を満たすか確認。
6. 必要な値(例:和)を計算して答える。
---
ご希望があれば、さらに難しいAIMEレベルの整数問題や、別パターン(剰余・合同式・不等式評価など)も出題・解説いたします!AlibabaのAPIキーを取得していない場合には、Alibaba Cloudから取得しましょう。
Qwen3-Max-Thinkingの活用事例
Qwen3-Max-Thinkingは、まだトレーニング中のプレビュー段階にあるものの、試験的な利用は始まっています。
ベースモデルの性能を引き継ぎつつ、論理的思考や段階的推論が強化されているため、数理解析・コード検証・自動化エージェントといった用途で注目を集めています。
数理・科学分野での推論タスク
AIMEやHMMTで満点を記録したことからもわかるように、Qwen3-Max-Thinkingは数学的・科学的推論において高い適性を示します。通常のLLMでは誤差が生じやすい長文計算や逐次推論でも、Thinkingモデルはコード実行を通じて結果を再検証できる点が評価。
コード解析・修正タスク
Instruct版と比較して、Thinking版は自己検証型のコード理解に優れています。
モデルが生成したプログラムを内部で実行し、実際の挙動を確認したうえで修正案を提示できるため、ソフトウェア開発支援において実験的に導入されています。特に「SWE-Bench Verified」のようなコード修正系タスクでは、エラー検知と修正パターンの説明を同時に行える点が強みです。
Qwen3-Max-Thinkingを実際に使ってみた
Qwen3-Max-Thinkingの特徴として優れた推論能力、並列思考、コードインタープリタなどが挙げられるので、それらを網羅していそうなタスクをAPI経由で実際に使ってみました。
1つ目のタスクは数学的推論能力の検証、2つ目のタスクはコード生成・デバッグ能力の検証です。
1つ目のタスクのサンプルコードはこちら
import requests
import json
import time
API_KEY = ""
URL = "https://dashscope-intl.aliyuncs.com/compatible-mode/v1/chat/completions"
def test_math_problem(problem, difficulty):
"""数学問題を投げて思考過程と回答を取得"""
payload = {
"model": "qwen3-max-preview",
"stream": False,
"messages": [
{"role": "system", "content": "あなたは数学の専門家です。問題を段階的に解いてください。"},
{"role": "user", "content": problem}
],
"extra_body": {
"enable_thinking": True,
"thinking_budget": 2048,
"enable_code_interpreter": True
}
}
headers = {
"Authorization": f"Bearer {API_KEY}",
"Content-Type": "application/json"
}
r = requests.post(URL, headers=headers, data=json.dumps(payload))
r.raise_for_status()
data = r.json()
content = data["choices"][0]["message"].get("content", "")
reasoning = data["choices"][0]["message"].get("reasoning_content", "")
return content, reasoning
problems = [
{
"difficulty": "Easy",
"problem": "1から100までの整数の和を求めてください。",
"expected": 5050
},
{
"difficulty": "Medium",
"problem": "方程式 x^3 - 6x^2 + 11x - 6 = 0 の整数解をすべて求めてください。",
"expected": [1, 2, 3]
},
{
"difficulty": "Hard",
"problem": "正の整数nについて、n^2を7で割った余りが2となる最小のnを求めてください。さらに、そのようなnの一般形を述べてください。",
"expected": 3
}
]
print("=" * 60)
print("数学的推論能力テスト")
print("=" * 60)
for i, test in enumerate(problems, 1):
print(f"\n【問題 {i}】難易度: {test['difficulty']}")
print(f"問題: {test['problem']}")
print(f"期待値: {test['expected']}")
print("-" * 60)
try:
content, reasoning = test_math_problem(test['problem'], test['difficulty'])
print("【回答】")
print(content)
if reasoning:
print("\n【思考過程の長さ】")
print(f"{len(reasoning)} 文字")
print("\n【思考過程(最初の500文字)】")
print(reasoning[:500] + "..." if len(reasoning) > 500 else reasoning)
print("\n" + "=" * 60)
time.sleep(1) # API制限対策
except Exception as e:
print(f"エラー: {e}")
print("=" * 60)
print("\n✓ テスト完了")結果はこちら
============================================================
数学的推論能力テスト
============================================================
【問題 1】難易度: Easy
問題: 1から100までの整数の和を求めてください。
期待値: 5050
------------------------------------------------------------
【回答】
1から100までの整数の和を求めるには、**等差数列の和の公式**を使います。
---
### 【等差数列の和の公式】
初項 \( a \)、末項 \( l \)、項数 \( n \) のとき、
\[
S = \frac{n}{2} \times (a + l)
\]
---
### 今回の問題に適用
- 初項 \( a = 1 \)
- 末項 \( l = 100 \)
- 項数 \( n = 100 \)(1から100までなので)
\[
S = \frac{100}{2} \times (1 + 100) = 50 \times 101 = 5050
\]
---
### 答え:
\[
\boxed{5050}
\]
---
💡 **豆知識**:この問題は、数学者ガウスが子供の頃に瞬時に解いたという有名な逸話があります。彼は1+100, 2+99, 3+98,...とペアを作って、それぞれが101になることに気づき、50ペアあるので50×101=5050と計算しました。
============================================================
【問題 2】難易度: Medium
問題: 方程式 x^3 - 6x^2 + 11x - 6 = 0 の整数解をすべて求めてください。
期待値: [1, 2, 3]
------------------------------------------------------------
【回答】
与えられた方程式は:
\[
x^3 - 6x^2 + 11x - 6 = 0
\]
これは**整数係数の3次方程式**なので、**有理数解(特に整数解)**は**有理根定理**を使って探すことができます。
---
### ステップ1:有理根定理を使う
有理根定理によると、
整数係数多項式 \( a_n x^n + \cdots + a_0 \) の有理数解 \( \frac{p}{q} \) は、
- \( p \) は定数項 \( a_0 \) の約数
- \( q \) は最高次の係数 \( a_n \) の約数
今回、定数項は \(-6\)、最高次の係数は \(1\) なので、
**有理数解の候補は \( \pm1, \pm2, \pm3, \pm6 \)** です。
整数解を探すので、これらの整数を代入して、実際に解になるか調べます。
---
### ステップ2:代入して確かめる
#### \( x = 1 \)
\[
1^3 - 6 \cdot 1^2 + 11 \cdot 1 - 6 = 1 - 6 + 11 - 6 = 0
\]
→ **解です!**
#### \( x = 2 \)
\[
8 - 24 + 22 - 6 = (8 - 24) + (22 - 6) = (-16) + 16 = 0
\]
→ **解です!**
#### \( x = 3 \)
\[
27 - 54 + 33 - 6 = (27 - 54) + (33 - 6) = (-27) + 27 = 0
\]
→ **解です!**
#### \( x = -1 \)
\[
-1 - 6 -11 -6 = -24 \neq 0
\]
#### \( x = 6 \)
\[
216 - 216 + 66 - 6 = 0 + 60 = 60 \neq 0
\]
#### \( x = -2, -3, -6 \) も同様に計算すると、明らかに正の項より負の項が大きく、0になりません。
---
### ステップ3:因数分解する
解が \( x=1,2,3 \) と分かったので、因数分解できます:
\[
x^3 - 6x^2 + 11x - 6 = (x - 1)(x - 2)(x - 3)
\]
展開して確認:
まず \( (x-1)(x-2) = x^2 - 3x + 2 \)
次に \( (x^2 - 3x + 2)(x - 3) \)
\[
= x^3 - 3x^2 - 3x^2 + 9x + 2x - 6 = x^3 - 6x^2 + 11x - 6
\]
→ 正しい!
---
### 結論:
この方程式の**整数解はすべて**:
\[
\boxed{1,\ 2,\ 3}
\]
============================================================
【問題 3】難易度: Hard
問題: 正の整数nについて、n^2を7で割った余りが2となる最小のnを求めてください。さらに、そのようなnの一般形を述べてください。
期待値: 3
------------------------------------------------------------
【回答】
正の整数 \( n \) について、\( n^2 \equiv 2 \pmod{7} \) となる最小の \( n \) を求め、さらにそのような \( n \) の一般形を導きます。
---
## ステップ1:法7における平方剰余を調べる
法7では、\( n \) の値は \( 0, 1, 2, 3, 4, 5, 6 \) のいずれかの剰余類に属します。それぞれの \( n \) に対して \( n^2 \bmod 7 \) を計算します。
\[
\begin{align*}
0^2 &\equiv 0 \pmod{7} \\
1^2 &\equiv 1 \pmod{7} \\
2^2 &\equiv 4 \pmod{7} \\
3^2 &\equiv 9 \equiv 2 \pmod{7} \quad \text{← ここ!} \\
4^2 &\equiv 16 \equiv 2 \pmod{7} \quad \text{← ここも!} \\
5^2 &\equiv 25 \equiv 4 \pmod{7} \\
6^2 &\equiv 36 \equiv 1 \pmod{7} \\
\end{align*}
\]
よって、
- \( n \equiv 3 \pmod{7} \) のとき \( n^2 \equiv 2 \pmod{7} \)
- \( n \equiv 4 \pmod{7} \) のとき \( n^2 \equiv 2 \pmod{7} \)
(※ \( 4 \equiv -3 \pmod{7} \) なので、平方すると同じ値になるのは当然)
---
## ステップ2:最小の正の整数 \( n \) を求める
上記より、\( n \equiv 3 \) または \( 4 \pmod{7} \) のときに条件を満たします。
最小の正の整数は \( \boxed{3} \) です(3 < 4)。
---
## ステップ3:一般形を求める
条件を満たす \( n \) は、7を法として3または4と合同な整数です。
つまり、
\[
n \equiv 3 \pmod{7} \quad \text{または} \quad n \equiv 4 \pmod{7}
\]
これは一つの式で表すこともできますが、「または」の関係なので、二つの合同式の和集合として表現するのが自然です。
あるいは、次のように書くこともできます:
\[
n \equiv \pm 3 \pmod{7}
\]
なぜなら \( 4 \equiv -3 \pmod{7} \) だからです。
---
## 最終的な答え
**最小の正の整数 \( n \)** は
\[
\boxed{3}
\]
**そのような \( n \) の一般形**は
\[
n \equiv 3 \pmod{7} \quad \text{または} \quad n \equiv 4 \pmod{7}
\]
あるいは
\[
n \equiv \pm 3 \pmod{7}
\]
---
✅ 以上で解答完了です。
============================================================
✓ テスト完了どのように思考してどのように解答に辿り着いたのかが一目瞭然ですね。処理時間としてもそこまで長くはありませんでした。
2つ目のタスクのサンプルコードはこちら
import requests
import json
import time
API_KEY = ""
URL = "https://dashscope-intl.aliyuncs.com/compatible-mode/v1/chat/completions"
def test_coding_task(task, task_type):
"""コーディングタスクを投げて結果を取得"""
payload = {
"model": "qwen3-max-preview",
"stream": False,
"messages": [
{"role": "system", "content": "あなたは優秀なプログラマーです。Pythonコードを書き、必要に応じて実行して結果を検証してください。"},
{"role": "user", "content": task}
],
"extra_body": {
"enable_thinking": True,
"thinking_budget": 1536,
"enable_code_interpreter": True
}
}
headers = {
"Authorization": f"Bearer {API_KEY}",
"Content-Type": "application/json"
}
r = requests.post(URL, headers=headers, data=json.dumps(payload))
r.raise_for_status()
data = r.json()
content = data["choices"][0]["message"].get("content", "")
reasoning = data["choices"][0]["message"].get("reasoning_content", "")
return content, reasoning
tasks = [
{
"type": "アルゴリズム実装",
"task": """
以下の要件を満たす関数を実装してください:
- 関数名: find_primes(n)
- 引数: 整数n
- 戻り値: n以下の素数のリスト
- 例: find_primes(20) → [2, 3, 5, 7, 11, 13, 17, 19]
実装後、n=50で実行して結果を表示してください。
"""
},
{
"type": "バグ修正",
"task": """
以下のコードにはバグがあります。バグを特定し、修正したコードを提示してください:
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-3)
# 期待: fibonacci(10) → 55
print(fibonacci(10))
バグを説明し、正しいコードを書いて実行結果も示してください。
"""
},
{
"type": "データ処理",
"task": """
以下のデータから分析を行ってください:
sales_data = [
{"month": "Jan", "sales": 15000, "costs": 8000},
{"month": "Feb", "sales": 18000, "costs": 9500},
{"month": "Mar", "sales": 22000, "costs": 11000},
{"month": "Apr", "sales": 19000, "costs": 10000},
]
1. 各月の利益(sales - costs)を計算
2. 最も利益が高かった月を特定
3. 平均利益を計算
Pythonコードで実装し、実行結果を表示してください。
"""
}
]
print("=" * 60)
print("コード生成・デバッグ能力テスト")
print("=" * 60)
for i, test in enumerate(tasks, 1):
print(f"\n【タスク {i}】タイプ: {test['type']}")
print(f"課題:")
print(test['task'])
print("-" * 60)
try:
content, reasoning = test_coding_task(test['task'], test['type'])
print("【生成されたコード・回答】")
print(content)
if reasoning:
print("\n【思考過程の長さ】")
print(f"{len(reasoning)} 文字")
print("\n【思考過程(最初の400文字)】")
print(reasoning[:400] + "..." if len(reasoning) > 400 else reasoning)
print("\n" + "=" * 60)
time.sleep(1) # API制限対策
except Exception as e:
print(f"エラー: {e}")
print("=" * 60)
print("\n✓ テスト完了")結果はこちら
============================================================
コード生成・デバッグ能力テスト
============================================================
【タスク 1】タイプ: アルゴリズム実装
課題:
以下の要件を満たす関数を実装してください:
- 関数名: find_primes(n)
- 引数: 整数n
- 戻り値: n以下の素数のリスト
- 例: find_primes(20) → [2, 3, 5, 7, 11, 13, 17, 19]
実装後、n=50で実行して結果を表示してください。
------------------------------------------------------------
【生成されたコード・回答】
```python
def find_primes(n):
"""
n以下の素数のリストを返す関数
Args:
n: 整数
Returns:
n以下の素数のリスト
"""
if n < 2:
return []
# エラトステネスの篩を使用
is_prime = [True] * (n + 1)
is_prime[0] = is_prime[1] = False # 0と1は素数ではない
for i in range(2, int(n**0.5) + 1):
if is_prime[i]:
# iの倍数を全てFalseにする
for j in range(i * i, n + 1, i):
is_prime[j] = False
# Trueのインデックス(素数)をリストにまとめて返す
primes = [i for i in range(2, n + 1) if is_prime[i]]
return primes
# n=50で実行して結果を表示
result = find_primes(50)
print(f"find_primes(50) = {result}")
```
```output
find_primes(50) = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]
```
エラトステネスの篩アルゴリズムを使用して、効率的に素数を求める関数を実装しました。このアルゴリズムは、各素数の倍数を順に除外していくことで、指定された数値以下のすべての素数を見つけることができます。
n=50で実行した結果、50以下の素数は `[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]` であることが確認できました。
============================================================
【タスク 2】タイプ: バグ修正
課題:
以下のコードにはバグがあります。バグを特定し、修正したコードを提示してください:
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-3)
# 期待: fibonacci(10) → 55
print(fibonacci(10))
バグを説明し、正しいコードを書いて実行結果も示してください。
------------------------------------------------------------
【生成されたコード・回答】
## バグの特定
このコードのバグは、フィボナッチ数列の再帰式が間違っている点です。
フィボナッチ数列の正しい定義は:
- F(0) = 0
- F(1) = 1
- F(n) = F(n-1) + F(n-2) (n ≥ 2)
しかし、コードでは `fibonacci(n-1) + fibonacci(n-3)` となっており、`n-2` ではなく `n-3` を使っています。
## 修正したコード
```python
def fibonacci(n):
if n <= 1:
return n
return fibonacci(n-1) + fibonacci(n-2) # n-3 を n-2 に修正
# 期待: fibonacci(10) → 55
print(fibonacci(10))
```
## 実行結果
```
55
```
## 補足説明
フィボナッチ数列は:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...
- F(0) = 0
- F(1) = 1
- F(2) = 1 (= 1 + 0)
- F(3) = 2 (= 1 + 1)
- F(4) = 3 (= 2 + 1)
- ...
- F(10) = 55 (= 34 + 21)
元のコードでは `n-3` を使っていたため、正しく計算できていませんでした。修正により、期待通りの結果55が得られます。
※ 注:この再帰実装は効率が悪いので、大きなnに対してはメモ化や反復的な実装が推奨されます。
============================================================
【タスク 3】タイプ: データ処理
課題:
以下のデータから分析を行ってください:
sales_data = [
{"month": "Jan", "sales": 15000, "costs": 8000},
{"month": "Feb", "sales": 18000, "costs": 9500},
{"month": "Mar", "sales": 22000, "costs": 11000},
{"month": "Apr", "sales": 19000, "costs": 10000},
]
1. 各月の利益(sales - costs)を計算
2. 最も利益が高かった月を特定
3. 平均利益を計算
Pythonコードで実装し、実行結果を表示してください。
------------------------------------------------------------
【生成されたコード・回答】
以下に、指定された分析をPythonコードで実装します。
```python
# データ定義
sales_data = [
{"month": "Jan", "sales": 15000, "costs": 8000},
{"month": "Feb", "sales": 18000, "costs": 9500},
{"month": "Mar", "sales": 22000, "costs": 11000},
{"month": "Apr", "sales": 19000, "costs": 10000},
]
# 1. 各月の利益を計算
print("1. 各月の利益:")
profits = []
for data in sales_data:
profit = data["sales"] - data["costs"]
profits.append(profit)
print(f"{data['month']}: {profit}")
# 2. 最も利益が高かった月を特定
max_profit = max(profits)
max_profit_index = profits.index(max_profit)
best_month = sales_data[max_profit_index]["month"]
print(f"\n2. 最も利益が高かった月: {best_month} (利益: {max_profit})")
# 3. 平均利益を計算
average_profit = sum(profits) / len(profits)
print(f"\n3. 平均利益: {average_profit}")
```
このコードを実行すると、以下の結果が得られます:
```
1. 各月の利益:
Jan: 7000
Feb: 8500
Mar: 11000
Apr: 9000
2. 最も利益が高かった月: Mar (利益: 11000)
3. 平均利益: 8875.0
```
**分析結果のまとめ:**
- 各月の利益は:1月(7000)、2月(8500)、3月(11000)、4月(9000)
- 最も利益が高かったのは3月で、利益は11,000でした
- 4ヶ月の平均利益は8,875でした
この分析により、3月が最も収益性の高い月であり、全体的な平均利益は8,875であることがわかりました。
============================================================
✓ テスト完了素数列挙アルゴリズム、バグ修正、データ処理の3タスクすべてで期待通りの結果を出力してくれています。特にバグ修正ではどこをどのように修正しているかを確認できるので、非常に有用だと感じます。
なお、コード生成特化型のオープンエージェントコーディングモデル【Qwen3‑Coder】について詳しく知りたい方は、下記の記事を合わせてご確認ください。
まとめ
本記事ではQwen3-Max-Previewの概要から仕組み、実際の使い方について解説をしました。まだ正式リリースではありませんが、性能が高く、今後の正式リリースが非常に楽しみなモデルです。
API経由でデモを行ってみましたが、数学・コーディング能力は高いなと感じました。本記事執筆段階(2025年11月8日)では、API経由で無料で利用できるのでご興味がある方はぜひ本記事を参考に利用してみてください。
最後に
いかがだったでしょうか?
AIの選定からPoC、社内運用まで、一貫した伴走支援が可能です。最適なAI活用方法を知りたい企業様は、お気軽にお問い合わせください。
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、大規模言語モデル(LLM)を対象に、言語理解能力、生成能力、応答速度の各側面について比較・検証した資料も配布しております。この機会にぜひご活用ください。






