OpenAI最新モデル「GPT-4.1」完全ガイド|業務活用・性能進化・料金まで解説
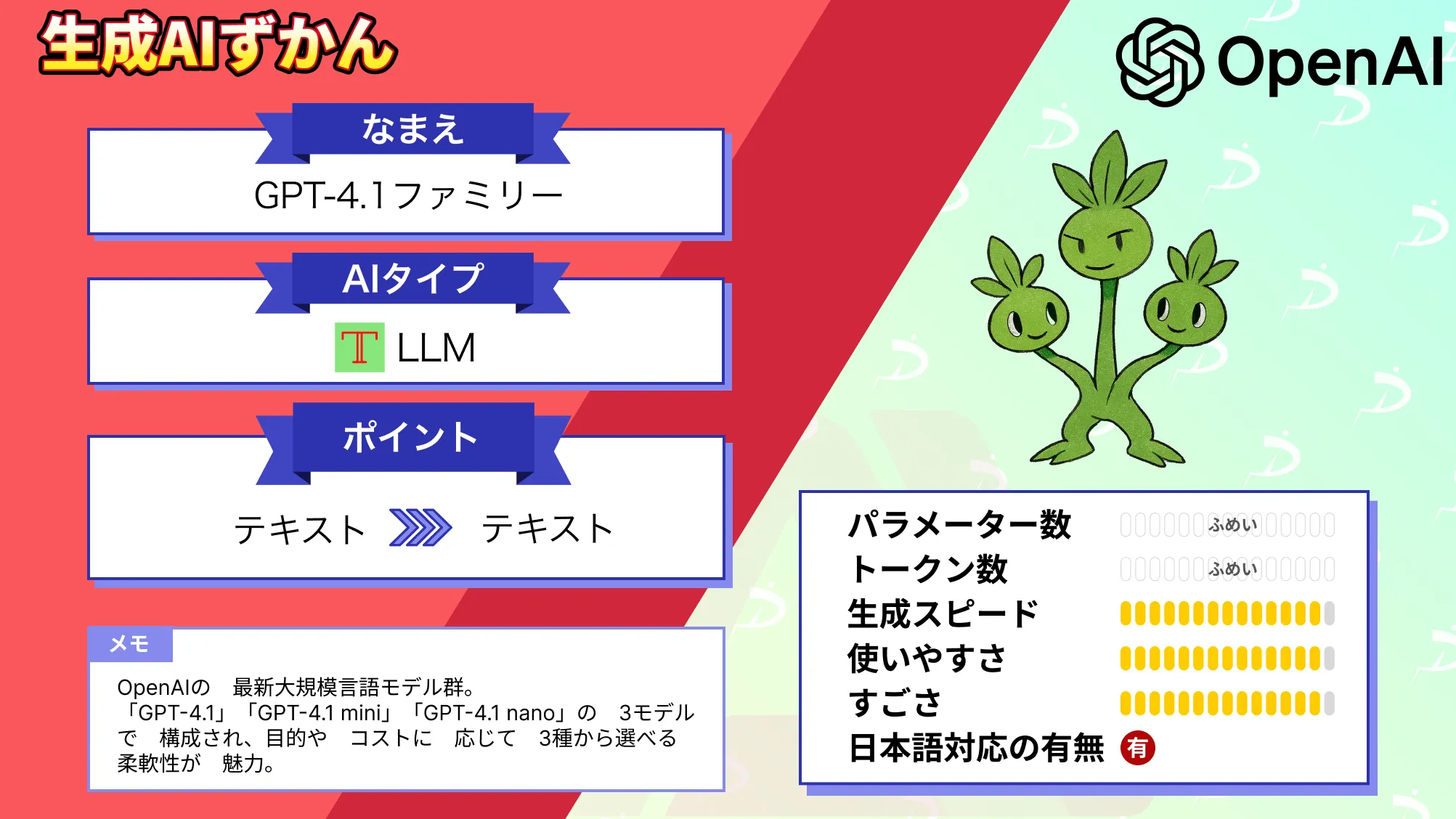
- OpenAI発の最新大規模言語ファミリーで3つのモデル群から構成される
- 従来のGPT-4oモデルと比べ、コーディング能力・指示追従性・長文脈処理の3分野で性能が飛躍的に向上
- 当初は開発者向けAPIのみだったが、ChatGPTから直接利用可能に
2025年4月15日、OpenAIがGPT-4.1ファミリーをリリースしました!
GPT-4.1ファミリーは、最新の大規模言語モデル群で、「GPT-4.1」「GPT-4.1 mini」「GPT-4.1 nano」の3モデルで構成されています。
従来のGPT-4o系モデルと比べ、コーディング能力・指示追従性・長文脈処理の3分野で飛躍的な性能向上が実現されているようです。
本記事では、GPT-4.1ファミリーの中でも特に「GPT-4.1」に焦点を当て、特徴から料金プラン、実際の使用例まで徹底解説します。ぜひ最後までご覧ください。
\生成AIを活用して業務プロセスを自動化/
GPT-4.1ファミリーとは?
GPT-4.1ファミリーは、OpenAIが公開した最新の大規模言語モデル群で、全モデルともに最大100万トークンまでの超長文コンテキストを扱うことができ、知識データベースも2024年6月時点まで更新されています。
以下では、各モデルの特徴や用途の違い、モデルサイズや推論速度について解説します。
GPT-4.1(標準モデル)
GPT-4.1は、ファミリーの中で最も高性能な「旗艦モデル」です。推論精度が非常に高く、コーディングや高度な推論を伴うタスクで突出した能力を示しています。
実際に、ソフトウェア開発ベンチマークの「SWE-bench Verified」では54.6%のタスク完了率を達成し、GPT-4oを21.4ポイント上回りました。
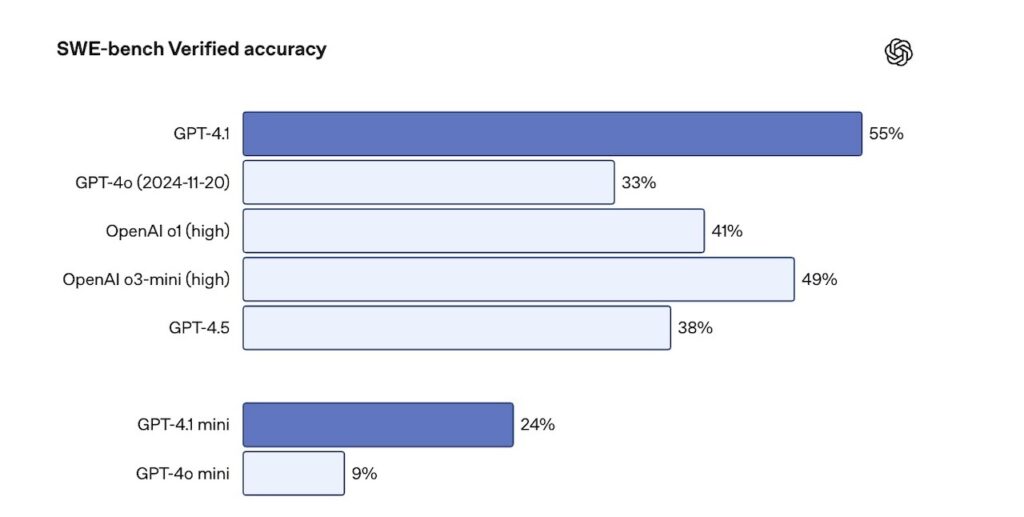
また、複雑な指示への対応力指標である「MultiChallenge」でも38.3%を記録し、GPT-4oから10.5ポイント改善しています。これらの結果から、GPT-4.1はコード生成やマルチステップの指示実行において現行トップクラスのモデルとなっています。
最大コンテキスト長が1Mトークンに拡大したことで、巨大なコードベースや長大なドキュメント内から必要な情報を的確に膨大な情報の中から必要な情報を見つけ出すことも可能です。
モデル規模が大きい分、推論レイテンシは他のファミリーモデルより長めではありますが、OpenAI社の最適化によりGPT-4o比で26%のコスト削減も実現しています。
GPT-4.1 mini
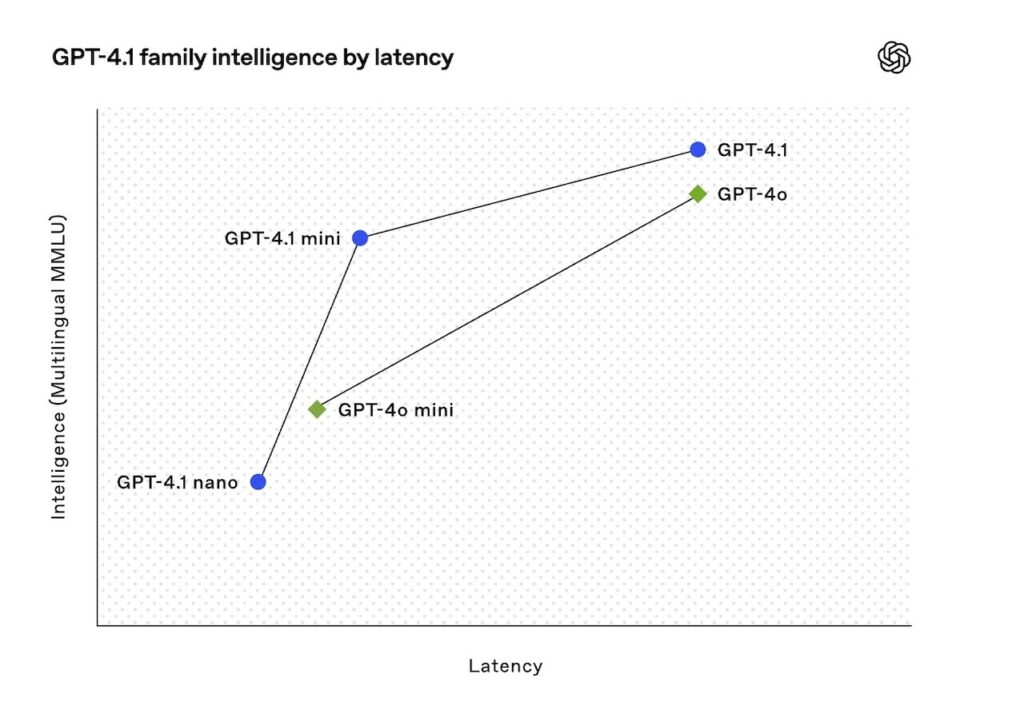
GPT-4.1 miniは小型化された高速モデルで、推論速度とコスト効率に優れます。レイテンシは、GPT-4oの約半分に短縮され、利用コストは83%も削減されています。
それにもかかわらず、総合的な知能評価ではGPT-4oを上回る性能を示し、数多くのベンチマークでGPT-4o並みかそれ以上のスコアを達成しています。特に、画像理解の分野ではGPT-4oを凌ぐ大幅な改善がOpenAI社から報告されており
、チャート・図表の読解などマルチモーダルな解析も得意とします。
GPT-4.1 miniはモデルサイズが抑えられているため応答が速く、長文入力(1Mトークン)への対応力も保持しています。
用途としては、高度な創造性や厳密な推論を要する場面では標準のGPT-4.1が適しますが、多くの一般的タスクでは品質を維持しつつ高速・低コストで応答できるGPT-4.1 miniが有力候補になっていきそうですね。
GPT-4.1 nano
GPT-4.1 nanoは、OpenAI初の「ナノ」モデルで、ファミリー最小・最速のモデルです。
推論の初回応答までの時間は驚異的に短く、例えば、128kトークンもの長文入力に対しても最初のトークンを5秒以内で返すことができます。
コストも非常に低く設定されており、大量のリクエスト処理やリアルタイム性が求められる低レイテンシ用途に適しています。モデルが小型でありながら知識水準は高く、大学レベルの知識テスト「MMLU」で80.1%というスコアを達成し、従来のGPT-4o miniを上回る学習度合いを示しました。
GPT-4.1 nanoも他モデル同様に、最大100万トークンの文脈を保持できるため、長い文章の要約や文書分類にも対応可能です。
特に、文章分類や自動補完など、高速応答が重視されるタスクで威力を発揮します。
ただし、モデル規模に起因する高度な推論力・創造性は上位モデルより抑えめのため、複雑な問題解決にはGPT-4.1またはminiを用い、nanoは補助的なタスクや簡易応答に使う、といった使い分けが想定されます。
GPT-4oとの違い
GPT-4.1は、従来のGPT-4oと比較して、コーディング性能・指示追従力・長文脈対応の3点で大きく進化しています。
まず、コーディング性能については、「SWE-bench Verified」のベンチマークでGPT-4oを約21ポイント上回り、より複雑で高度なコード生成やバグ修正が可能になっています。
指示追従力においても、「MultiChallenge」でGPT-4oより約10ポイント高いスコアを達成し、より複雑で曖昧な要求にも的確に対応できるようになりました。
さらに、最大1Mトークンの長文脈処理能力を持つため、従来モデルでは不可能だった大量の情報を一括して扱えます。
これによって、実務でのドキュメント解析やチャットの履歴を参照した高度な応答など、幅広い業務領域での活用が可能になっています。
では、これらの特徴をもう少し詳しくみていきましょう。
GPT-4.1の特徴
GPT-4.1は従来のGPT-4oより性能が大幅に進化しています。
上述の通り、特にコーディング性能・指示追従力・長文脈対応の3つが大きく改善され、実務における活用範囲が広がりました。
ここからは、具体的な性能を客観的に示す「SWE-bench Verified」のスコアや、指示追従力を示す「MultiChallenge」の結果、さらに1Mトークンという長文脈に対応したメリット、コスト効率や応答速度(レイテンシ)の改善点を詳しくご紹介していきます。
コーディング性能
GPT-4.1は、コーディング性能が特に強化されており、「SWE-bench Verified」ベンチマークにおいてGPT-4oを大きく上回るスコアを達成しました。
具体的には、54.6%という高い正答率を記録しており、GPT-4oの33.2%から21.4ポイントの向上となっています。
この性能アップにより、従来は困難だった複雑なプログラミングタスクやエラー修正、コード生成が迅速かつ正確に行えるようになりました。
特に企業の開発チームにおいては、開発時間の短縮や生産性の向上に直結する性能改善と言えます。
指示追従力
GPT-4.1は、指示追従力においても大幅に進化しています。
指示理解の総合評価ベンチマークである「MultiChallenge」においては、GPT-4.1は38.3%というハイスコアを達成し、GPT-4oの27.8%から10.5ポイント向上しました。
これは、より複雑で曖昧な指示でも、明確に意図を捉えて期待通りのアウトプットを生成できることを示しています。
この改善によって、ビジネスや教育現場での質問応答の精度が向上し、より信頼性の高い結果を得られるようになっています。
長文脈対応
GPT-4.1は、最大1Mトークンという超長文脈への対応を実現しています。
この長文脈処理能力によって、極めて大規模なテキスト情報やコードベース全体を入力として扱えるようになりました。
例えば、膨大な仕様書や技術ドキュメントを一括で読み込み、的確な要約や解析が可能になるほか、長期間にわたるチャット履歴を参照した応答生成にも役立ちます。
この進化によって、業務の効率化や精度向上に大きく貢献できるシーンが増えるでしょう。
コスト効率・レイテンシの最適化
GPT-4.1では、推論パイプラインを刷新し、計算グラフの再利用や内部キャッシュ効率を高めたことで、従来比で最大83%のコスト削減と約50%のレイテンシ短縮を実現しています。
特に、軽量モデルのGPT-4.1 miniにおいては、入出力トークン単価が大幅に低く設定され、リアルタイム応答が求められるチャットボットや教育向けQAシステムに適しています。
さらにダイナミックバッチングとトークン再配置アルゴリズムにより、大規模リクエスト処理時でもスループットが向上します。
グラフ化すると、コスト軸と速度軸の両面で右下方向に大きく改善していることが一目でわかります。
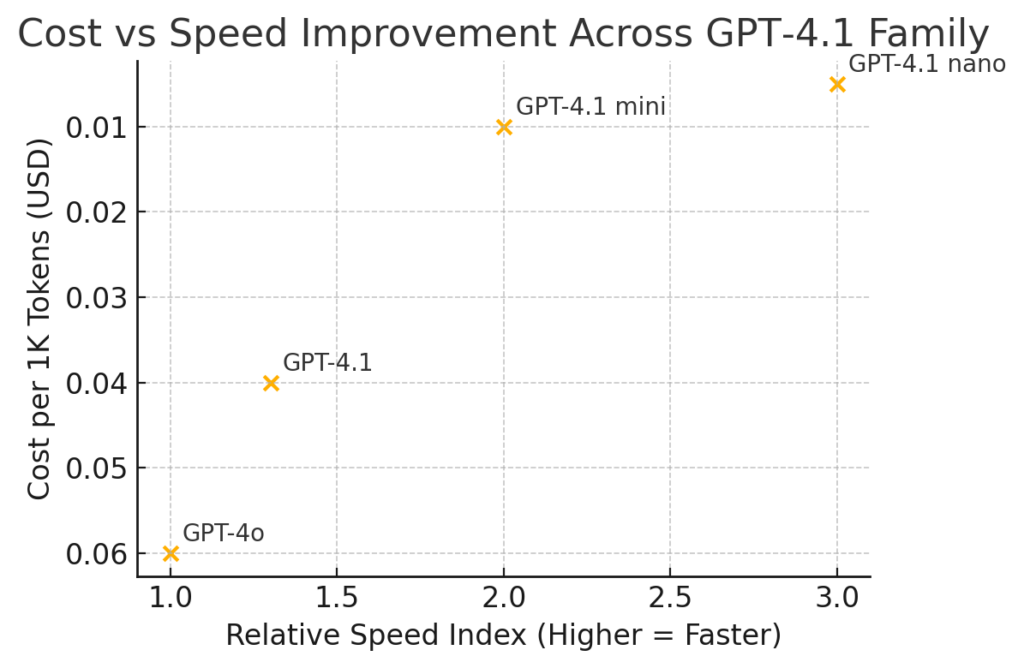
横軸が「相対スピード指標」(値が大きいほど高速)で、縦軸が「1 Kトークン当たりのコスト(USD)」(下ほど低コスト)となっています。
GPT-4.1ファミリーの違いと使い分け
GPT-4.1 vs GPT-4.1 mini vs GPT-4.1 nano
GPT-4.1ファミリーは、モデルごとに明確な性能差があり、適した用途も異なります。
『GPT-4.1』はファミリーの中で最も性能が高く、高精度な推論や複雑なコード生成、長文脈を扱う業務で圧倒的な力を発揮します。
一方、『GPT-4.1 mini』は、性能とコスト・処理速度のバランスが最適化されているモデルで、リアルタイム性が重要な対話システムや教育現場での質疑応答など、多くの一般的な用途に適しています。
そして最も小型の『GPT-4.1 nano』は、簡単なタスクや迅速なレスポンスが求められる場面に特化したモデルであり、軽量のチャットボットや短いテキストの分類などに有効です。
このように各モデルは目的に応じた特性を持つため、利用シーンに応じて性能・速度・コストのバランスを考慮し、最適なモデルを選択することが重要になります。
ユースケース別の推奨モデル例(業務・教育・研究・チャットボットなど)
利用するモデルは具体的なユースケースにより異なります。
『業務用』においては、高度なプログラミング支援や長文ドキュメント解析に対応可能なGPT-4.1(標準モデル)が最も推奨されます。
一方、『教育現場』においては、レスポンス速度とコスト効率が重要であり、GPT-4.1 miniが適しています。GPT-4.1 miniを使用することで、質問応答システムやリアルタイムでのフィードバックに十分な性能を発揮しつつ、コストも抑えることができます。
『研究用途』においては、迅速にアイデアを試すプロトタイプ開発や実験的なタスクを行う際にGPT-4.1 miniやnanoが推奨されます。さらに、『チャットボット』や簡易的な『顧客サポート』など、軽量かつ高速な処理が求められる用途にはGPT-4.1 nanoがベストな選択となります。
よくある使い分けの失敗パターンと解説
GPT-4.1ファミリーのモデル選択に失敗すると、業務効率の低下や不要なコスト増加を引き起こします。
よく見られる失敗例として、高精度を求めるタスクに対してコスト削減を狙い、最も軽量なGPT-4.1 nanoを採用してしまうケースがあります。
この場合、モデルの推論能力が不足して精度の低い回答が頻発し、業務の品質低下を招きます。
逆に、全ての用途において高性能なGPT-4.1を選択すると、軽量な処理でも高額なコストがかかり、応答速度が求められるサービスではレスポンス遅延の問題が生じます。
モデルを選定する際には、各モデルの性能特性を明確に理解し、用途に応じた性能・コスト・速度のバランスを考慮した慎重な検討を行う必要があります。
実際の利用場面に即した評価を行うことが、失敗を回避するポイントです。
使い方
GPT-4.1ファミリーの利用方法は、ChatGPTのインターフェースから直接利用する方法と、OpenAI API経由で利用する方法(およびAPI Playgroundを用いる方法)があります。
ChatGPT上での使い方
OpenAIは2025年5月、ChatGPT Plus/Proユーザー向けにGPT-4.1モデルを直接選択できる機能をリリースしました。その利用方法は非常に簡単です。
1.ChatGPTにログイン
まず、ChatGPTのPlusまたはProプランに加入し、ChatGPTのWebまたはモバイルアプリにログインします。無料プランの場合はGPT-4.1を直接選択することはできません。
2.モデルを選択
チャット画面上部のモデル選択ドロップダウンから「GPT-4.1」もしくは「GPT-4.1 mini」を選択します(※Plusユーザーは「GPT-4」を選ぶと自動的にGPT-4.1が使われます)。以下画像のように、モデル一覧の「More models」セクションに表示されています。
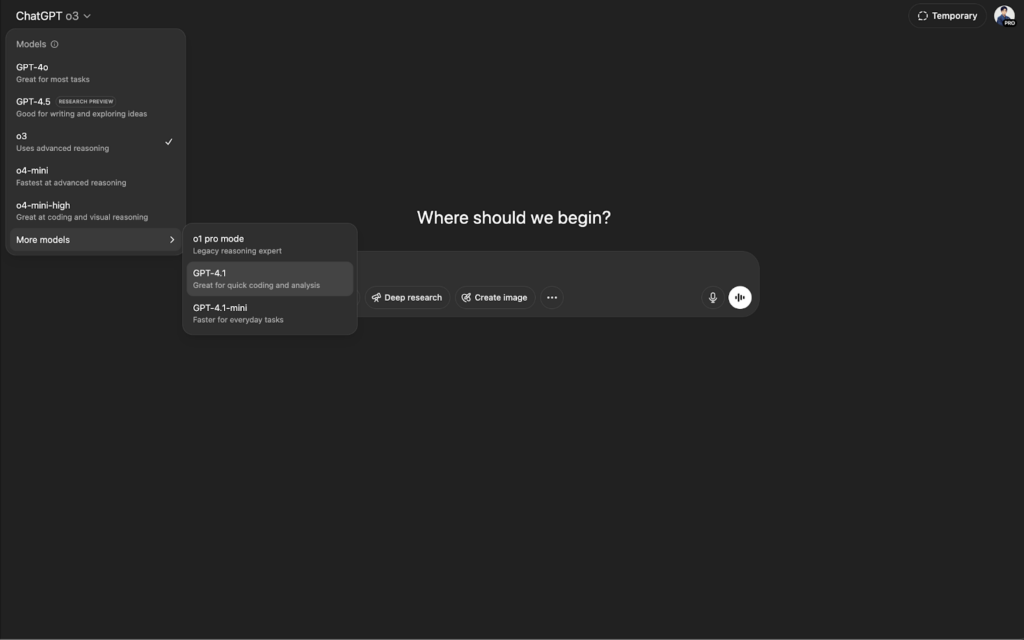
3.プロンプトを入力して対話
あとは通常のChatGPTと同様に入力欄にプロンプト(質問や依頼内容)を送信するだけです。
GPT-4.1モデルはGPT-4oより応答が高速で、コーディングなどの高度なタスクにも強いため、APIを使わなくてもChatGPT上で高度な生成AI機能を試せるのが大きなメリットです。
例えば、長文の要約や複雑なプログラミング質問にも、ChatGPT上でそのままGPT-4.1が対応してくれます。
OpenAI API経由での使い方
1.API利用登録とキー取得:OpenAIの開発者向けプラットフォームにアクセスし、APIキーを取得します。すでにOpenAIアカウントがあればダッシュボードの「API Keys」からシークレットキーを発行可能です。新規の場合はクレジットカード登録で一定の無料利用枠も提供されます。
2.API呼び出しの実装:開発環境でOpenAIのAPIを呼び出すコードを記述します。公式のAPIドキュメントやSDK(Python用のopenaiライブラリなど)を参考に、エンドポイントにリクエストを送ります。
ChatGPTと同様のChat Completion APIを使う場合、モデル名にgpt-4.1(またはgpt-4.1-miniやgpt-4.1-nano)を指定し、messagesフィールドにユーザ発話やシステム命令を含むJSONをPOSTします。例えばPythonでは以下のようなコードになります。
import openai
openai.api_key = "YOUR_API_KEY"
response = openai.ChatCompletion.create(
model="gpt-4.1",
messages=[{"role": "user", "content": "...(ユーザの質問)..."}]
)
print(response.choices[0].message["content"])3.アプリケーションへの統合:API呼び出しで期待どおりの応答が得られたら、必要に応じて自社のアプリケーションやサービスに組み込みます。プロンプトの調整やパラメータ(例えば温度temperatureの設定など)も行い、要件に合った形でGPT-4.1の機能を統合してください。
OpenAI API Playground上での使い方
OpenAIが提供しているWebベースのPlayground (https://platform.openai.com/playground/prompts?models=gpt-4.1)を使うと、コードを書くことなく直感的にプロンプトを試すことができます。
1.OpenAIアカウントでログイン:OpenAIダッシュボードにアクセスし、ログイン後「Playground」メニューを開きます。
2.モデルの選択:Playground画面上部の「モデル選択ドロップダウン」から「GPT-4.1」「GPT-4.1 mini」「GPT-4.1 nano」のいずれかを選択。
3.パラメータ設定:テンプレート(チャット/完了)を選ぶか、あるいは手動でtemperatureやmax_tokensなどを調整できます。システムロールを付与したい場合は「System」などの追加フィールドに指示を書き込みます。
4.プロンプト入力:メインのエディタ領域にユーザーの質問や命令文を入力します。
「Submit」ボタンをクリック:即座にGPT-4.1モデルの応答が画面右側(または下部のレスポンス欄)に表示されます。
5.応答の確認・編集:Playground上で出力結果を見ながらプロンプトを修正し、再度「Submit」することで何度でも試行錯誤できます。
6.コードへの転用:気に入った設定・プロンプトを保存し、画面右側の「View code」などを使うと、その設定を使ったAPI呼び出しコード(Pythonやcurlなど)を自動生成できます。それをコピーして自社アプリやスクリプトに貼り付ければ、同等の動作をプログラム上で再現可能です。
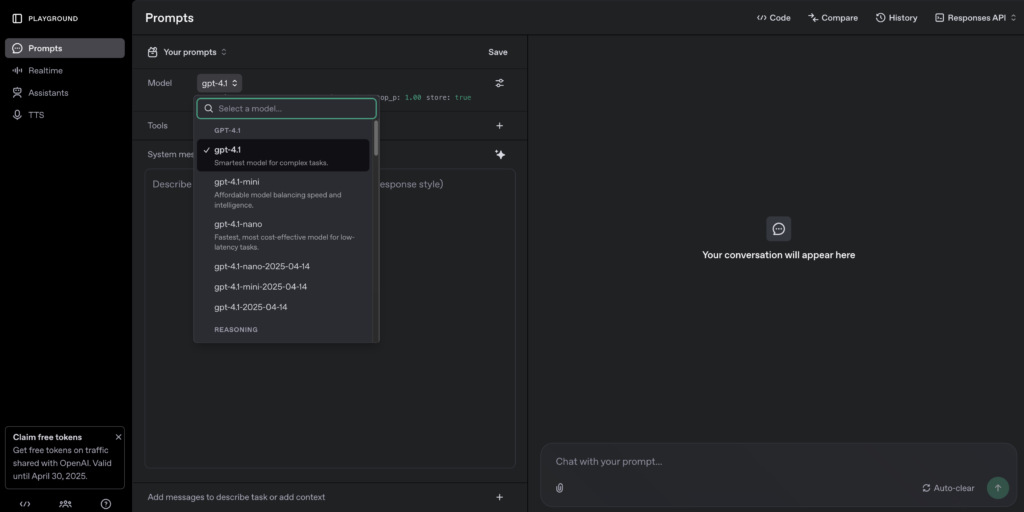
PlaygroundはGUIで設定しやすく、さらにリアルタイムで応答を見られるため、プロンプト作成やパラメータ調整の学習ツールとして最適です。十分にプロンプトを調整・検証したうえで、APIや自社アプリで実装すると効率的な開発ができます。
GPT-4.1の料金プラン
GPT-4.1ファミリーを利用する際の料金体系について、ChatGPTサービス(サブスクリプション)とOpenAI API(従量課金)の両面から整理します。
ChatGPTのプランと料金
2025年4月15日時点では、Webインターフェースやモバイルアプリ上でユーザーが直接GPT-4.1モデルを選択することはできませんでしたが、2025年5月中旬のアップデートにより、ChatGPTのWebインターフェース上でユーザーが直接『GPT-4.1モデル』を選択できるようになりました。
現在、ChatGPT Plus・Pro・Teamなどの有料プラン利用者は、チャット画面のモデル選択メニュー(More models欄)からGPT-4.1を選択して利用できます。
以下は、ChatGPTの主なプラン体系と料金・利用条件の概要です。
| プラン | 料金(税込) | 内容 |
|---|---|---|
| 無料 | 無料 | 誰でも利用可能な基本プラン。GPT-3.5(Turbo)モデルによるチャットが利用できます。GPT-4系モデルは使用不可。一定の使用制限あり(過負荷時の応答遅延など)。 |
| Plus | $20/月(¥2,700) | |
| Pro | $200/月(¥30,000) | 上位ヘビーユーザー向けの高額プラン。最新の最良モデルへの無制限アクセスが特徴で、GPT-4.1ファミリーを含むOpenAIの最高性能モデルや音声機能を制限なく利用可能。大量の問い合わせや高速応答を必要とするプロユーザ・開発者向け。 |
| Enterprise | 要問い合わせ (カスタム契約) | 企業向けの包括プラン。組織単位でChatGPTを導入するもので、無制限のGPT-4利用に加え、ビジネス向けのデータプライバシー保証や管理者機能を備える。価格は利用規模に応じた個別見積もり。 |
GPT-4.1 API利用料金
今回リリースされたGPT-4.1ファミリーは、開発者向けAPIを通じてのみ提供されていました。
OpenAIは「GPT-4.1はAPIのみで提供し、ChatGPTではGPT-4oに改良を段階的に取り込む」と発表していましたが、ユーザーからの人気を受けて方針転換し、ChatGPTでも直接利用可能となったようです。
それでも、現在もAPI経由での提供は継続されており、開発者や企業はOpenAI APIを通じてGPT-4.1ファミリーを利用可能です。
OpenAI API Playgroundに加え、リリース直後からGitHub CopilotやCursor、Windsurfなどの開発支援ツールでもGPT-4.1の利用サポートが進んでいます。
OpenAIのAPIを利用してGPT-4.1ファミリーのモデルにアクセスする場合は、使用したトークン数に応じた従量課金制となります(クレジットカード課金または事前チャージ残高からの消費)。
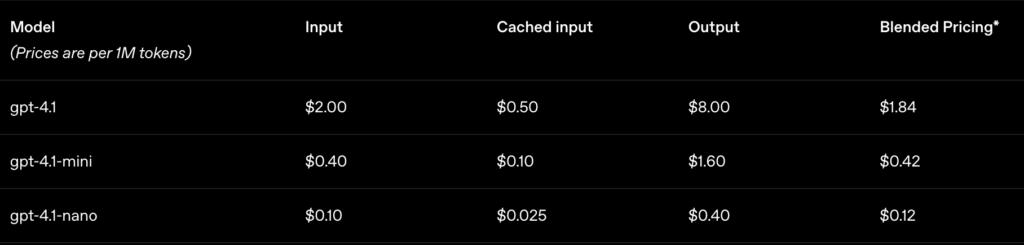
各モデルのAPI料金(1Mトークンあたりの単価)は以下の通りです。
※入力と出力で単価が異なりますが、長文コンテキストを使用しても追加料金は発生せず、標準のトークン単価のみで利用可能となっています。
GPT-4.1のライセンス
GPT-4.1ファミリーは、OpenAIが提供するクローズドソースのAPIサービスであり、利用にはOpenAIの利用規約に従う必要があります。
以下の表に、商用利用・改変・再配布・特許利用・私的利用の各観点でのライセンス上の可否をまとめます。
| 利用用途 | 可否 | 備考 |
|---|---|---|
| 商用利用 | ⭕️ | |
| 改変 | 🔺 | モデルそのもののコードや重みへの直接アクセスは提供されないため直接改変は不可。 |
| 配布 | 🔺 | 第三者へモデルそのものを共有・転売することは不可。 |
| 特許使用 | ⭕️ | |
| 私的使用 | ⭕️ |
商用利用、私的利用ともに可能ですが、モデルそのものの改変や再配布は禁止されており、サービスを通じた利用に限られています。
GPT-4.1 vs GPT-4o 性能検証してみた
今回は、「GPT-4.1」と「GPT-4o」に対して、同じ動作環境(OpenAI API Playground)で、2種類のタスクを振って性能比較をしていきます!
コーディング・アルゴリズム実装
プロンプト(目的:アルゴリズムロジックの正確性、生成コードの品質、コメントの適切さ)
重み付きグラフにおける最短経路を見つけるダイクストラ法をJavaで実装してください。主要なステップを説明するコメントを含めてください。GPT-4o 結果
import java.util.*;
// Graphのエッジを表現するクラス
class Edge {
int targetVertex;
int weight;
public Edge(int targetVertex, int weight) {
this.targetVertex = targetVertex;
this.weight = weight;
}
}
// ダイクストラ法を実装するクラス
class Dijkstra {
// グラフの全頂点数
private int vertices;
// 隣接リストでグラフを表現
private List<List<Edge>> adjList;
public Dijkstra(int vertices) {
this.vertices = vertices;
// 初期化
adjList = new ArrayList<>();
for (int i = 0; i < vertices; i++) {
adjList.add(new ArrayList<>());
}
}
// グラフにエッジを追加するメソッド
public void addEdge(int source, int target, int weight) {
adjList.get(source).add(new Edge(target, weight));
}
// ダイクストラのアルゴリズム
public void dijkstra(int startVertex) {
// 各頂点への最短距離を格納する配列
int[] distances = new int[vertices];
// 全ての距離を無限大(もしくは十分大きな数)で初期化
Arrays.fill(distances, Integer.MAX_VALUE);
// 始点の距離は0
distances[startVertex] = 0;
// 最小ヒープを使用して次に処理する頂点を決定
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(Comparator.comparingInt(e -> e.weight));
// 始点をキューに追加
priorityQueue.add(new Edge(startVertex, 0));
while (!priorityQueue.isEmpty()) {
// 最小距離の頂点を取り出す
Edge currentEdge = priorityQueue.poll();
int currentVertex = currentEdge.targetVertex;
// 現在の頂点に接続された辺をすべて探索
for (Edge edge : adjList.get(currentVertex)) {
int neighborVertex = edge.targetVertex;
int newDist = distances[currentVertex] + edge.weight;
// より短いパスが見つかった場合
if (newDist < distances[neighborVertex]) {
distances[neighborVertex] = newDist;
priorityQueue.add(new Edge(neighborVertex, newDist));
}
}
}
// 最短経路の結果を出力
printShortestPaths(startVertex, distances);
}
// 最短距離を出力
private void printShortestPaths(int startVertex, int[] distances) {
System.out.println("Vertex\t\tDistance from Source " + startVertex);
for (int i = 0; i < vertices; i++) {
System.out.println(i + "\t\t" + distances[i]);
}
}
// メインメソッド
public static void main(String[] args) {
int vertices = 5;
Dijkstra graph = new Dijkstra(vertices);
// エッジを追加
graph.addEdge(0, 1, 9);
graph.addEdge(0, 2, 6);
graph.addEdge(0, 3, 5);
graph.addEdge(0, 4, 3);
graph.addEdge(2, 1, 2);
graph.addEdge(2, 3, 4);
// ダイクストラ法を実行
graph.dijkstra(0);
}
}GPT-4.1 結果
import java.util.*;
public class DijkstraAlgorithm {
// 辺を表すクラス
static class Edge {
int to, weight;
Edge(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
// ダイクストラ法を実行するメソッド
public static int[] dijkstra(List<List<Edge>> graph, int start) {
int n = graph.size();
int[] dist = new int[n]; // 各頂点への最短距離
Arrays.fill(dist, Integer.MAX_VALUE);
dist[start] = 0;
PriorityQueue<int[]> pq = new PriorityQueue<>(Comparator.comparingInt(a -> a[0]));
pq.add(new int[]{0, start}); // {現在の距離, 頂点}
while (!pq.isEmpty()) {
int[] current = pq.poll();
int curDist = current[0], u = current[1];
// より短い経路がすでに見つかっている場合はスキップ
if (curDist > dist[u])
continue;
// 隣接する頂点をすべて確認
for (Edge edge : graph.get(u)) {
int v = edge.to;
int weight = edge.weight;
// より短い経路が見つかった場合は更新
if (dist[v] > dist[u] + weight) {
dist[v] = dist[u] + weight;
pq.add(new int[]{dist[v], v});
}
}
}
return dist;
}
// サンプルのメイン処理
public static void main(String[] args) {
int n = 5; // 頂点数
List<List<Edge>> graph = new ArrayList<>();
for (int i = 0; i < n; i++) graph.add(new ArrayList<>());
// グラフ構築(例:双方向)
graph.get(0).add(new Edge(1, 2));
graph.get(0).add(new Edge(2, 4));
graph.get(1).add(new Edge(2, 1));
graph.get(1).add(new Edge(3, 7));
graph.get(2).add(new Edge(4, 3));
graph.get(3).add(new Edge(4, 1));
// 必要なら逆方向も追加
int start = 0;
int[] dist = dijkstra(graph, start);
// 結果を出力
for (int i = 0; i < n; i++) {
System.out.println("頂点 " + i + " までの最短距離: " + dist[i]);
}
}
}回答生成時間はそれぞれ約12秒ほどで大差ありませんでしたが、出力は異なっていますね。詳細は割愛しますが、GPT-4.1のほうがシンプルなコード設計となっており、可読性の観点で優れているように感じます。
数学
プロンプト(目的:論理的思考力、問題解決能力、段階的な説明能力の検証)
午前8時にA駅を出発し、時速60マイルで300マイル離れたB駅に向かう列車があります。午前9時にB駅を出発し、時速75マイルで平行な線路をA駅に向かう別の列車があります。2つの列車は何時に出会いますか?ステップバイステップで推論を示してください。GPT-4o 結果
列車Aと列車Bが出会う時間を求めるために、それぞれの列車が出発してからの距離を計算します。
列車Aの距離を式で表す。
出発時間: 午前8時
速度: 60マイル/時
距離(マイル) = 60 × 時間(時間)
列車Bの距離を式で表す。
出発時間: 午前9時
速度: 75マイル/時
距離(マイル) = 75 × (時間 - 1)
※午前9時に出発するので、A駅を出発してからの時間は1時間後になります。
出会う条件を設定する。
列車Aの距離 + 列車Bの距離 = 300マイル
60t + 75(t - 1) = 300
方程式を解く。
60t + 75t - 75 = 300
135t - 75 = 300
135t = 375
t = 375 / 135
t = 2.777... 時間
時間を分に変換。
0.777... × 60 ≈ 46.67分
列車が出会う時刻を求める。
午前8時から2時間46分後なので、午前10時46分に出会います。
したがって、2つの列車は午前10時46分に出会います。GPT-4.1 結果
この問題を順を追って解いていきましょう。
1. 移動する列車の出発時刻と速度
A駅発(A→B方向):午前8時出発、時速60マイル
B駅発(B→A方向):午前9時出発、時速75マイル
両駅の距離は 300マイル です。
2. 各列車の動きを整理
8時〜9時(A駅発の列車だけが進む)
8時から9時まで、A駅発の列車だけが進む。
その1時間で進む距離は: ( 60 \text{マイル/時} \times 1 \text{時間} = 60 \text{マイル} )
9時になった時点で、A駅発の列車はすでにA駅から60マイル進んでいる。
残りのA駅〜B駅間の距離は: ( 300 - 60 = 240 \text{マイル} )
3. 9時以降、2台の列車が向かい合って進む
両列車の合計接近速度: ( 60 \text{マイル/時} + 75 \text{マイル/時} = 135 \text{マイル/時} )
残り240マイルをこの速度で近づいていく。
4. 出会うまでの時間を計算
必要な時間:
( \frac{240 \text{マイル}}{135 \text{マイル/時}} = \frac{240}{135} = \frac{16}{9} \approx 1.78 \text{時間} )
1時間は60分なので
( 0.78 \times 60 \approx 47 )分
よって、9時から1時間47分後に出会う。
5. 出会う時刻
( 9:00 + 1:47 = 10:47 )
まとめ
2つの列車は午前10時47分に出会います。
【計算手順のまとめ】
8〜9時はA駅発のみが動き60マイル進む(残り240マイル)。
9時から合計135マイル/時で近づく。
240 ÷ 135 = 約1.78時間 ≒ 1時間47分
9:00 + 1:47 = 10:47GPT-4.1の結果のほうが、計算手順が明確になっていますね。
プロンプトの「ステップ・バイ・ステップで」という指示を忠実に再現しており、箇条書きで丁寧に推論過程を説明してくれています。このようにGPT-4.1は指示追従性が高く、家庭の説明もわかりやすい回答を返してくれることが確認できました。
気になる方は、他のより複雑なタスクでぜひ試してみてください。
まとめ
GPT-4.1ファミリーは、総合的な知能・推論力で従来モデルを大きく上回りつつ、目的やコストに応じて3種のモデルから選べる柔軟性が魅力です。
特にGPT-4.1はあらゆる面で性能が向上しており、開発者にとって協力なツールとなっています。また、2025年5月中旬のアップデートで、ChatGPT上から直接GPT-4.1を利用できるようになったことで、エンジニアでなくとも最新モデルの恩恵を受けられるようになりました。
Playground、あるいはAPIを介して使い始めるハードルも低く、商用利用や私的利用にも幅広く対応しています。
今後さらにアップデートが進む中で、GPT-4.1ファミリーは開発者の生産性向上だけでなく、教育・研究・ビジネス活用など、多岐にわたる領域で存在感を増していくことが予想されます。
ぜひ、一度試用してみて、その圧倒的な性能と利便性を体感してみてください!

最後に
いかがだったでしょうか?
ChatGPTは単なるチャットツールではなく、議事録要約やFAQ自動化、コードレビュー、商品説明文の自動生成など、すでに多くの企業が実務で活用を始めています。
「自社の業務でも使えるのか?」「どのモデルが最適か?」といった検討に、実際のユースケースや導入事例をもとにご提案が可能です。
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、大規模言語モデル(LLM)を対象に、言語理解能力、生成能力、応答速度の各側面について比較・検証した資料も配布しております。この機会にぜひご活用ください。





