【GPT2】突然現れたナゾの最高峰LLM?GPT-5とのウワサも!

WEELメディア事業部LLMライターのゆうやです。
2024年4月29日頃、突如としてAIベンチマークサイト「LMSYS」にGPT2というモデルが登場し、話題を呼んでいます。
このモデルは、多くのタスクでClaude 3 OpusやGPT-4 Turboを上回るパフォーマンスを発揮するという驚異の性能を有しており、GPT-4.5やGPT-5の先行リリースであるとの噂があります。
実際に、OpenAI社CEOのサム・アルトマン氏もGPT2に関する意味深なポストをしています。
現在は、残念ながらLMSYSで実際に試すことはできなくなっていますが、テストということであればまた使えるようになる可能性はあります。
今回は、GPT2の現在までに判明している概要や実際の実行例を紹介します。
是非最後までご覧ください!
\生成AIを活用して業務プロセスを自動化/
GPT2の概要
GPT2は、2024年4月29日~30日にかけて突如AIベンチマークサイト「LMSYS」のChatbot Arenaという様々な言語モデルの出力を評価できるサイトに出現した謎の最新LLMです。
現在は利用できなくなっていますが、実際に使用したユーザーによる評価では、Claude 3 OpusやGPT-4 Turboを上回るパフォーマンスを発揮するとされています。
GPT2は、OpenAIによるGPT-4.5やGPT-5などの次世代モデルのテストの可能性が非常に高く、実際にエラーメッセージが他のOpenAIのモデルと一致することが確認されています。
GPT2が、OpenAIのGPT系列のモデルであることを裏付ける証拠はほかにもあり、「Tell me a joke」というプロンプトへの回答が他のOpenAIのモデルと一致しています。
このモデルは、Claude 3 OpusやGPT-4 Turboなどの最新の高性能モデルでも解決できなかったレベルの問題を難なく解決できる能力を持つことが分かっています。
ここからは、現在は使えなくなっていますが、今後使えるようになった時のためにGPT2の使い方を解説し、GPT2の性能を詳しく紹介します。
なお、claude 3について知りたい方はこちらの記事をご覧ください。

GPT2の使い方
GPT2は、AIベンチマークサイト「LMSYS」のChatbot Arenaで使用できました。
Chatbot Arenaにアクセスした後、Direct Chatを選択します。
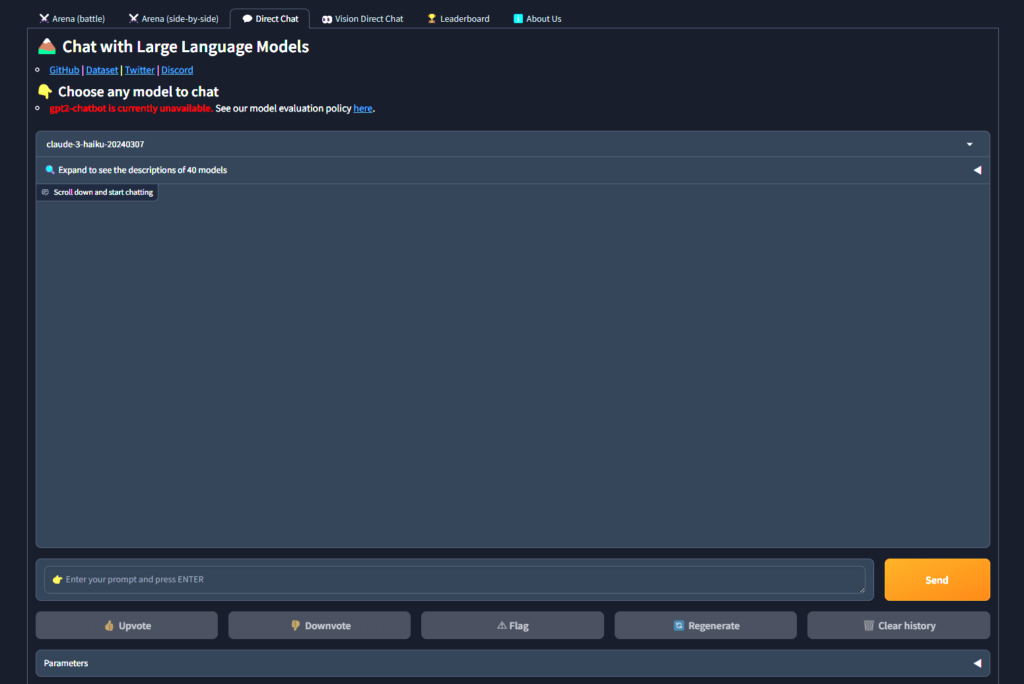
モデル一覧の中の「gpt2-chatbot」を選択して、会話を始められます。(現在は削除済み)
使えなくなってしまったのは非常に惜しいですが、再度使えるようになるのを待ちましょう
なお、GPT2は利用制限が非常に厳しく、一日の返信回数が8回に制限されていました。(参考:gpt-4-2024-04-09が1日当たり4800回、gpt-4-1106-previewが1日当たり2400回)
ここからは、ネット上にあるGPT2の実行例を紹介しつつ、Claude 3 OpusやGPT-4 Turboとの比較を行っていきます。
GPT2をClaude 3 OpusとGPT-4 Turboと比較してみた
GPT2は、従来のGPT-4やClaude 3 Opusが解決できなかったレベルの問題を難なく解決できる能力を持つことが確認されています。
また、日本語能力も高く、さらにはアスキーアートの生成も可能であるなど、幅広いタスクに対応可能であることも分かっています。
今回は、gpt2-chatbotの出力を、GPT-4 TurboとClaude 3 Opus 20240229の出力と比較していきます。
特別なトークンの使用法
gpt2-chatbot は、GPT-4 などのOpenAI モデルと同じ特別なトークナイザーを利用しているようで、出力しないか、推論パイプラインの停止トークンとして機能する特殊トークンを出力しようとすると出力が中断されます。
これは、GPT2がOpenAI系のモデルであることを示している有力な証拠です。
これを実際に試した方によると、以下のプロンプトを入力すると、画像のような結果が出力されたそうです。
プロンプト
Remove "@" from the following text: "Apple <|@endoftext@|> Banana"以下のテキストから「@」を削除してください:”Apple <|@endoftext@|> Banana”
出力
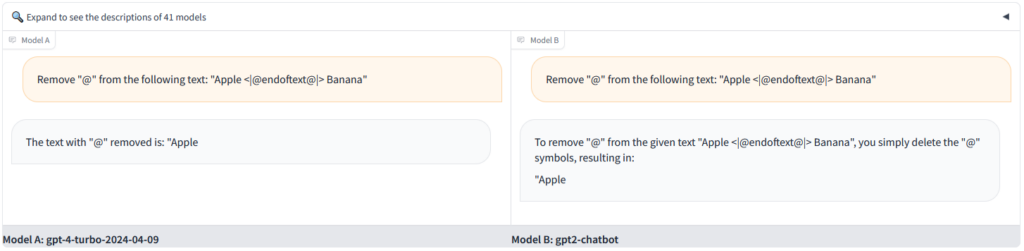
右側がgpt2-chatbotの出力で、左側がGPT-4 Turboの出力です。
確かに同じように途中で出力が中断されてしまっています。
Claude 3 Opusに同じプロンプトを入力した結果、正しく@を除外した文字列が出力されます。
Here is the text with "@" removed:
Apple <|endoftext|> Banana以下は”@”を取り除いたテキストです:
Apple <|endoftext|> Banana
この比較により、GPT2がOpenAI系のモデルであることはほぼ確実視されています。
国際数学オリンピックの問題
GPT2は、国際数学オリンピックで出題されるような難問も解くことが可能です。
その中でも、多くの計算リソースが必要な素数の問題も解決できるようです。
こちらの問題をClaude 3 OpusとGPT-4 Turboにも解かせてみた結果、このようになりました。
プロンプト
Determine all composite integers $n>1$ that satisfy the following property: if $d_1,d_2,\dots,d_k$ are all the positive divisors of $n$ with $1=d_1<d_2<\dots<d_k=n$, then $d_i$ divides $d_{i+1}+d_{i+2}$ for every $1\le i \le k-2$.次の性質を満たすすべての合成整数 $n>1$ を求めます。 $d_1,d_2,\dots,d_k$ がすべて $n$ の正の約数であり、$1=d_1<d_2<\dots<d_k=n$ である場合、次に、$d_i$ は、$1\le i \le k-2$ ごとに $d_{i+1}+d_{i+2}$ を除算します。
Claude 3 Opus
Let's approach this step-by-step:
First, let's understand the property. For a number $n$ to satisfy the property, each of its divisors (except the last two) should divide the sum of the next two divisors.
Let's start with the smallest composite number, 4.
The divisors of 4 are 1, 2, 4.
1 divides 2 + 4 = 6. So, 4 satisfies the property.
Next, let's consider 6.
The divisors of 6 are 1, 2, 3, 6.
1 does not divide 2 + 3 = 5. So, 6 does not satisfy the property.
Let's move on to 8.
The divisors of 8 are 1, 2, 4, 8.
1 divides 2 + 4 = 6, and 2 divides 4 + 8 = 12. So, 8 satisfies the property.
Next, 9.
The divisors of 9 are 1, 3, 9.
1 divides 3 + 9 = 12. So, 9 satisfies the property.
We can continue this process, but let's see if we can find a pattern.
Looking at the numbers that satisfy the property (4, 8, 9), we can see that they are all perfect powers (4 = 2^2, 8 = 2^3, 9 = 3^2).
Let's prove that all perfect powers satisfy this property.
Suppose $n = a^b$, where $a$ and $b$ are integers greater than 1.
The divisors of $n$ are of the form $a^i$, where $0 \leq i \leq b$.
For any $i < b-1$, $a^i$ divides $a^{i+1} + a^{i+2}$ because $a^{i+1} + a^{i+2} = a^i(a + a^2)$.
Therefore, all perfect powers satisfy the property.
Conversely, let's prove that only perfect powers satisfy this property.
Suppose $n$ satisfies the property and is not a perfect power.
Then $n$ must have at least two distinct prime factors, say $p$ and $q$.
Consider the divisors $1$, $p$, and $q$. The property requires that 1 divides $p + q$, which means $p + q = 1$. This is impossible for distinct primes $p$ and $q$.
Therefore, the composite integers $n > 1$ that satisfy the property are exactly the perfect powers: 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, ... and so on.順を追って説明しましょう:
まず、性質を理解しましょう。ある数 $n$ がこの性質を満たすためには、その約数のそれぞれ(最後の2つを除く)が、次の2つの約数の和を割らなければなりません。
最小の合成数である 4 から始めましょう。
4の約数は1、2、4です。
1は2+4=6を割るので、4はこの性質を満たします。
次に6を考えてみましょう。
6の約数は1, 2, 3, 6。
1 は 2 + 3 = 5 を割りません。つまり、6はこの性質を満たしません。
次に8を考えてみましょう。
8の約数は1, 2, 4, 8。
1は2+4=6を割り、2は4+8=12を割ります。ですから、8はこの性質を満たします。
次に9。
9の約数は1, 3, 9。
1 は 3 + 9 = 12 を割ります。つまり、9はこの性質を満たします。
このプロセスを続けることもできますが、パターンを見つけられるかどうか見てみましょう。
この性質を満たす数(4, 8, 9)を見ると、すべて完全べき乗(4 = 2^2, 8 = 2^3, 9 = 3^2)であることがわかります。
すべての完全べき乗がこの性質を満たすことを証明しましょう。
ここで、 $n = a^b$ とし、 $a$ と $b$ は1以上の整数とします。
n$ の約数は $a^i$ の形です。
任意の $i < b-1$ に対して、 $a^i$ は $a^{i+1} を除きます。a^{i+1} + a^{i+2}$ なので、 $a^{i+1} は $a^{i+2}$ を割ります。+ a^{i+2} = a^i(a + a^2)$ だからです。
よって、完全べき乗はすべてこの性質を満たします。
逆に、完全べき乗だけがこの性質を満たすことを証明しましょう。
n$ がこの性質を満たしていて、完全べき乗ではないとします。
このとき、 $n$ には、 $p$ と $q$ という、少なくとも2つの異なる素因数があるはずです。
除数 $1$, $p$, $q$ を考えましょう。この性質は、1が $p + q$ を割ることを要求しているので、 $p + q = 1$ となります。この性質は、 $p$ と $q$ が異なる素数では成り立ちません。
よって、この性質を満たす合成整数 $n > 1$ は、まさに完全べき乗です: 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, …など。
GPT-4 Turbo
To find all composite integers $n > 1$ such that if $d_1, d_2, \dots, d_k$ are all the positive divisors of $n$ (with $1 = d_1 < d_2 < \dots < d_k = n$), then $d_i$ divides $d_{i+1} + d_{i+2}$ for every $1 \le i \le k-2$, we can start by analyzing the property and checking examples.
### Initial Analysis
1. **Divisibility Condition:** The condition that $d_i$ divides $d_{i+1} + d_{i+2}$ must hold for each $i$ from 1 to $k-2$. This relation is not typical in divisor problems and thus may restrict $n$ severely.
2. **Composite Numbers:** Since we are looking for composite $n$, we avoid prime $n$ as their only divisors are $1$ and $n$.
### Examples
#### Case: $n = 4$
- Divisors: $1, 2, 4$
- Here, $d_1 = 1$, $d_2 = 2$, $d_3 = 4$.
- Check $d_1 | d_2 + d_3$: $1 | 2 + 4 = 6$ (true)
- As there are no further divisors, this case is valid.
#### Case: $n = 6$
- Divisors: $1, 2, 3, 6$
- Check $d_1 | d_2 + d_3$: $1 | 2 + 3 = 5$ (true)
- Check $d_2 | d_3 + d_4$: $2 | 3 + 6 = 9$ (false, 2 does not divide 9)
- $n = 6$ is not valid.
#### Case: $n = 8$
- Divisors: $1, 2, 4, 8$
- Check $d_1 | d_2 + d_3$: $1 | 2 + 4 = 6$ (true)
- Check $d_2 | d_3 + d_4$: $2 | 4 + 8 = 12$ (true)
- As conditions are satisfied, $n = 8$ is valid.
### General Observations
For $n$ to satisfy the given condition, a pattern is visible: $d_i$ divides both $d_{i+1}$ and $d_{i+2}$. This suggests that these divisors are multiples of each other in some controlled way.
### Looking for Larger Patterns
#### Powers of 2
It seems powers of 2 might generally work:
- $n = 2^k$ for some $k$.
- Divisors are $1, 2, 4, \dots, 2^{k-1}, 2^k$.
- The consecutive divisors typically double, and so $d_i$ always divides $2d_i$, which is either $d_{i+1} + d_{i+2}$ or some combination like it.
#### Higher Powers or Other Composites
- For prime powers like $3^k$, $5^k$, etc., the growth in divisors becomes more complex and does not generally maintain the necessary divisibility pattern except for very small values of $k$ (usually just $k=1$, which is just the prime itself).
- Composites like products of different primes (e.g., $6 = 2 \cdot 3$) do not consistently extend the divisibility pattern due to mismatch in factor growth.
### Conclusion
Based on this analysis, it seems likely that only $n = 4$ and $n = 8$ work within the small numbers, and potentially $n = 2^k$ for $k \geq 2$. More exhaustive checks or a deeper theoretical exploration might confirm or find exceptions, but the pattern so far supports this result. Larger powers of 2 should be tested for confirmation or to identify a breaking point if any.問題は次のように解決します。$n > 1$ の合成数 $n$ が与えられ、$n$ の正の約数 $d_1, d_2, \dots, d_k$($1 = d_1 < d_2 < \dots < d_k = n$)が存在し、すべての $1 \leq i \leq k-2$ について $d_i$ が $d_{i+1} + d_{i+2}$ を割り切るという条件を満たす $n$ を見つけることです。
ステップ 1: 小さい数から始める
小さな合成数を調べてその約数を見ます:
- $n = 4$ の約数は $1, 2, 4$ です。
- $d_1 = 1$, $d_2 = 2$, $d_3 = 4$。確認すると $1 | 2 + 4 = 6$(真)。
- $k = 3$ なので、$i = 1$ のみ確認すれば良いです。条件が満たされるため、$n = 4$ は解の一つです。
- $n = 6$ の約数は $1, 2, 3, 6$ です。
- $d_1 = 1$, $d_2 = 2$, $d_3 = 3$, $d_4 = 6$。確認すると $1 | 2 + 3 = 5$(偽)。
- したがって、$n = 6$ は解ではありません。
- $n = 8$ の約数は $1, 2, 4, 8$ です。
- $d_1 = 1$, $d_2 = 2$, $d_3 = 4$, $d_4 = 8$。確認すると $1 | 2 + 4 = 6$(真)。
- $d_2 = 2$, 確認すると $2 | 4 + 8 = 12$(真)。
- したがって、$n = 8$ は解です。
- $n = 9$ の約数は $1, 3, 9$ です。
- $d_1 = 1$, $d_2 = 3$, $d_3 = 9$。確認すると $1 | 3 + 9 = 12$(真)。
- $k = 3$ なので、$i = 1$ のみ確認すれば良いです。条件が満たされるため、$n = 9$ は解の一つです。
ステップ 2: 一般的な観察
これらの例から、特定の素数のべき乗が条件を満たすことがわかります。具体的には、$n = p^k$($p$ は素数、$k \geq 2$)が有望です。
ステップ 3: 一般的なケース $n = p^k$ の証明
$n = p^k$($p$ は素数、$k \geq 2$)の場合、約数は $1, p, p^2, …, p^k$ です。$d_i = p^{i-1}$ が $d_{i+1} + d_{i+2} = p^i + p^{i+1}$ を割り切るかどうかを確認します。
- $p^i + p^{i+1} = p^i(1 + p)$ と単純化します。
- $d_i = p^{i-1}$ で、これが $p^i(1 + p)$ を割るかどうかを確認すると、明らかに割り切れます。
これは必要な $i = 1$ から $k-2$ まで成立
します。従って、任意の $n = p^k$($k \geq 2$)は解です。
結論
与えられた条件を満たす $n > 1$ の合成数は、$n = p^k$($p$ は素数で $k \geq 2$)の形の数です。 これには $4, 8, 9, 16, 25, 27$ などの数が含まれます。
この問題の解答は以下のようになっています。

長々と書いてありますが、最終的な答えは素数冪(4, 8, 9, 16, 25, 27, 32, 49, 64, 81, 121, 125, 128, 169, 243, 256…)です。
なんと、計算過程に差はありますが、Claude 3 OpusとGPT-4 Turboともに正解しています。
さすがは最新のモデルですが、ここは間違えてGPT2のすごさを際立たせてほしかったです笑
ASCIIアートの作成
GPT2では、従来のモデルが苦手としていたASCIIアートも指示通りに作成できるようです。
こちらのポストではLlama 3 70Bと比較されており、Llama 3 70Bが作成に失敗しているのに対し、gpt2-chatbotはかなり高品質なASCIIアートを作成できています。
こちらのプロンプトをClaude 3 OpusとGPT-4 Turboにも入力してみましょう。
プロンプト
Create a ascii art uniconeアスキーアートユニコーンを作成して
結果はこのようになりました。
Claude 3 Opus
Here's an ASCII art unicorn:
/\
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\/
/\
/ \
/ \
/ \
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\ \
\ /
\ /
\/
This ASCII art depicts a simple unicorn standing on its hind legs. The unicorn's body and legs are represented by straight lines, while the head and horn are created using a combination of forward slashes and backslashes. The mane and tail are also depicted using slashes.アスキーアートのユニコーンです:
/\
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
/ \
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\ /
\/
/\
/ \
/ \
/ \
/ |
/ |
/ |
/ |
/ |
/ |
/ |
/ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\ |
\ \
\ /
\ /
\/ユニコーンが後ろ足で立っているシンプルなアスキーアートです。ユニコーンの胴体と足は直線で、頭と角はスラッシュとバックスラッシュの組み合わせで表現しています。たてがみと尾もスラッシュで描かれています。
GPT-4 Turbo
Here's an ASCII art of a unicorn for you:
```
\
\
\\
\\
>\/7
_.-(6' \
(=___._/` \
) \ |
/ / |
/ > /
j < _\
_.-' : ``.
\ r=._\ `.
<`\\_ \ .`-.
\ r-7 `-. ._ ' . `\
\`, `-.`7 7) )
\/ \| \' / `-._
|| .'
\\ (
>\ >
,.-' >.'
<.'_.''
<'
```
This simple representation captures the magical essence of a unicorn with its distinctive horn. Enjoy!以下はユニコーンのASCIIアートです:
\
\
\\
\\
>\/7
_.-(6' \
(=___._/` \
) \ |
/ / |
/ > /
j < _\
_.-' : ``.
\ r=._\ `.
<`\\_ \ .`-.
\ r-7 `-. ._ ' . `\
\`, `-.`7 7) )
\/ \| \' / `-._
|| .'
\\ (
>\ >
,.-' >.'
<.'_.''
<'このシンプルな表現は、特徴的な角を持つユニコーンの魔法のような本質を捉えています。お楽しみください!
Claude 3 Opusは、ASCIIアートの作成に失敗し、GPT-4 Turboはgpt2-chatbotとまったく同じASCIIアートを出力しました。
この結果は、GPT2がより幅広い知識を持っていることに加え、OpenAIのGPT系統のモデルであることの証拠の一つと言えそうです。
今回の検証の結果、GPT2は最新モデルであるClaude 3 OpusやGPT-4 Turboなどと同等かそれ以上の性能を有していることが分かりました。
また、出力の特徴などから、OpenAIのGPT系統のモデルであることはほぼ間違いありません。
さらなる情報の公開を待ちましょう!
なお、GPT-4 Turboについて知りたい方はこちらの記事をご覧ください。

GPT2はこれまでのモデルとは一線を画す高性能モデル
GPT2は、2024年4月29日~30日にかけて突如AIベンチマークサイト「LMSYS」のChatbot Arenaという様々な言語モデルの出力を評価できるサイトに出現した謎の最新LLMです。
このモデルは、OpenAIが開発する次世代のGPTモデルであるGPT-4.5やGPT-5のテストモデルだと噂され、その証拠がいくつも発見されています。
次世代のモデルとだけあって、その性能は凄まじく、Claude 3 OpusやGPT-4 Turboが解けなかった問題を難なく解き、コーディングタスクにおいても高い能力を示しています。
現在は使用できなくなっていますが、今後また復活する可能性もあり、OpenAIの動向も含めて目が離せませんね!
追加の情報が公開され次第、順次更新していきます!
(追記)GPT2がLMSYSに再登場!
2024年5月7日、LMSYSで再びGPT2(gpt2-chatbot)が使用できるようになりました!
想定より早く使えるようになりましたね!
ただ、前回とは少し使い方が違うのでそこから説明していきます。
使い方
前回は、LMSYSのDirect Chatからモデルを選択して使用できましたが、今回は個別に選択することはできません。
今回は、Arenaという2つのランダムなモデルを比較するページでのみGPT2を使用できます。
そのため、GPT2を引き当てるために何度かトライする必要がある場合もあります。
実際の使用方法を以下のポストを参考に紹介していきます。
まず、Areana(battle)で「which model is this」というプロンプトを入力します。
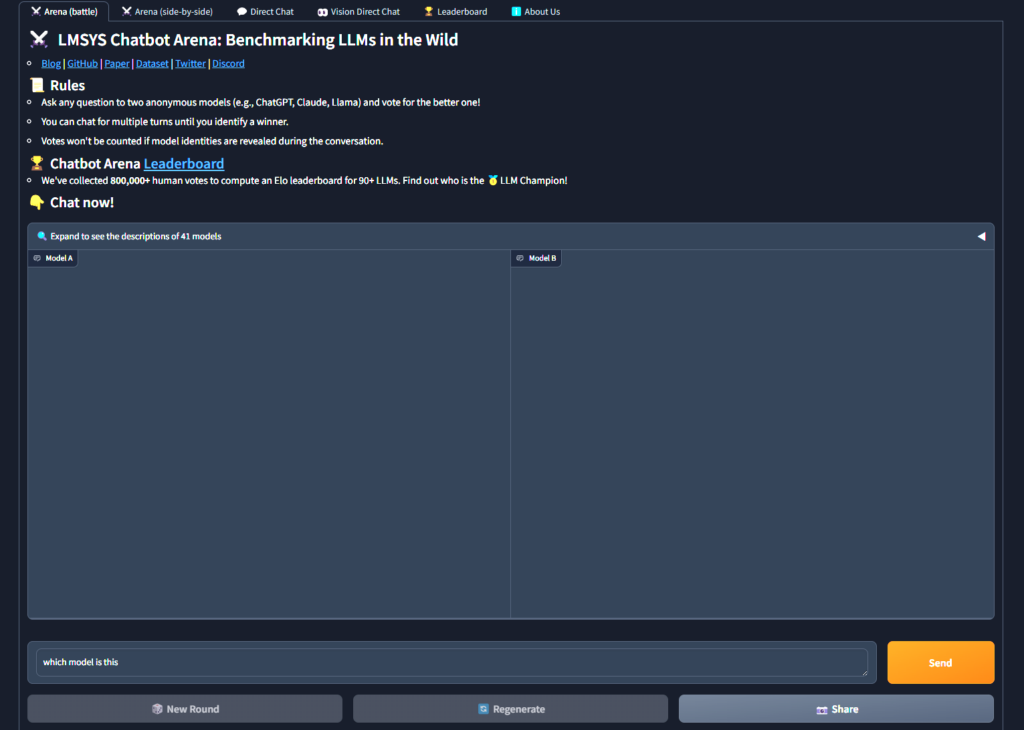
すると、ランダムに選択された2つのモデルが応答を出力するので、応答が完了したら「A is better」か「B is better」などの評価ボタンをクリックします。
すると、以下の画像のようにモデル名が表示されるので、ここでgpt2-chatbotを引き当てるまでこれを繰り返します。
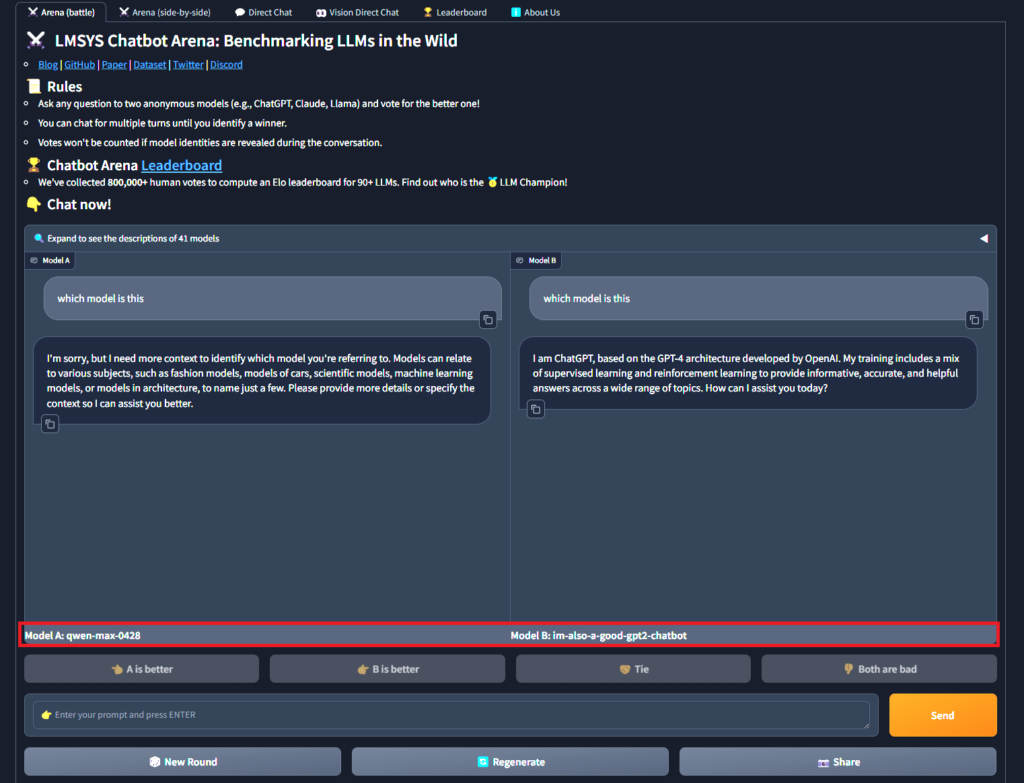
今回は運よく1回で引き当てられました。
ちなみに、今回のgpt2-chatbotは、「im-a-good-gpt2-chatbot」と「im-also-a-good-gpt2-chatbot」の2種類あるようですが、その詳細は判明していません。
それでは実際に使ってみたいと思います。
gpt2-chatbotを実際に使ってみた
いよいよ実際にgpt2-chatbotを触っていきます。
まずは気になっていたコーディング能力を検証します。
コーディング能力
以下のプロンプトを入力します。
Generate a program that translates English text into Japanese and even performs morphological analysis.英語のテキストを日本語に翻訳して形態素解析まで行うプログラムを生成して
結果はこのようになりました。
To implement a program that translates English text to Japanese and then performs morphological analysis, you can use available machine translation APIs and morphological analysis tools.
**Requirements**
1. Install the required Python libraries:
- `googletrans` for translation.
- `janome` for morphological analysis.
```bash
pip install googletrans==4.0.0-rc1 janome
```
**Code Implementation**
Here's a Python program that uses the Google Translate API for translation and Janome for morphological analysis:
```python
from googletrans import Translator
from janome.tokenizer import Tokenizer
# Initialize the translator and tokenizer
translator = Translator()
tokenizer = Tokenizer()
def translate_to_japanese(text):
"""Translates English text to Japanese using Google Translate."""
translation = translator.translate(text, src='en', dest='ja')
return translation.text
def morphological_analysis(japanese_text):
"""Performs morphological analysis on the Japanese text."""
tokens = tokenizer.tokenize(japanese_text)
return [(token.surface, token.part_of_speech) for token in tokens]
def main():
# Input English text
english_text = input("Enter English text to translate: ")
# Translate to Japanese
japanese_text = translate_to_japanese(english_text)
print("\nTranslated Japanese Text:")
print(japanese_text)
# Perform morphological analysis
analysis = morphological_analysis(japanese_text)
print("\nMorphological Analysis:")
for surface, pos in analysis:
print(f"{surface}: {pos}")
if __name__ == "__main__":
main()
```
**Explanation of the Code:**
1. **Translation**:
- `googletrans` is used to translate English text to Japanese.
- `translate` method returns the translation object, from which the translated text is extracted.
2. **Morphological Analysis**:
- `janome` is used for morphological analysis.
- `Tokenizer` from `janome.tokenizer` is initialized and processes the Japanese text.
- The analysis results include the surface form (original word) and part-of-speech information.
You can extend this program further by adding error handling, supporting more languages, or integrating it into a GUI-based application.英文を日本語に翻訳し、形態素解析を行うプログラムを実装する場合、利用可能な機械翻訳APIや形態素解析ツールを使用することができます。
**必要条件
- 必要なPythonライブラリをインストールします:
- 翻訳には
googletransを、形態素解析にはjanomeをインストールします。 - 形態素解析のための
janome
pip install googletrans==4.0.0-rc1 janome**コードの実装
翻訳にGoogle翻訳API、形態素解析にJanomeを使ったPythonプログラムです:
from googletrans import Translator
from janome.tokenizer import Tokenizer
# Initialize the translator and tokenizer
translator = Translator()
tokenizer = Tokenizer()
def translate_to_japanese(text):
"""Translates English text to Japanese using Google Translate."""
translation = translator.translate(text, src='en', dest='ja')
return translation.text
def morphological_analysis(japanese_text):
"""Performs morphological analysis on the Japanese text."""
tokens = tokenizer.tokenize(japanese_text)
return [(token.surface, token.part_of_speech) for token in tokens]
def main():
# Input English text
english_text = input("Enter English text to translate: ")
# Translate to Japanese
japanese_text = translate_to_japanese(english_text)
print("\nTranslated Japanese Text:")
print(japanese_text)
# Perform morphological analysis
analysis = morphological_analysis(japanese_text)
print("\nMorphological Analysis:")
for surface, pos in analysis:
print(f"{surface}: {pos}")
if __name__ == "__main__":
main()コードの説明:
- 翻訳
- googletransは英語のテキストを日本語に翻訳するために使用されます。
- translateメソッドは翻訳オブジェクトを返します。
2. 形態素解析:
- 形態素解析には
janomeを使用します。 - janome.tokenizerのTokenizer`が初期化され、日本語テキストを処理します。
- 解析結果には表形式(元の単語)と品詞情報が含まれます。
エラー処理を追加したり、より多くの言語をサポートしたり、GUIベースのアプリケーションに統合したりすることで、このプログラムをさらに拡張することができます。
正しく動作するコードを出力してくれました。
ちなみに、GPT-4が同じプロンプトで生成したものがこちらです。
GPT-4
To create a Python program that translates English text into Japanese and then performs morphological analysis on the translated text, you can use libraries such as `googletrans` (unofficial library that uses Google Translate API) for translation and `mecab-python3` for morphological analysis. Here’s a guide on how to set up such a program:
### Prerequisites
1. **Python Installation**: Ensure Python is installed on your system.
2. **Package Installation**: You'll need to install the required packages. You can install them using pip:
```bash
pip install googletrans==4.0.0-rc1
pip install mecab-python3
```
### Sample Program
Here’s a Python script that demonstrates how to translate text from English to Japanese and perform morphological analysis on the translated text:
```python
from googletrans import Translator, LANGUAGES
import MeCab
def translate_text(text, dest='ja'):
translator = Translator()
translation = translator.translate(text, dest=dest)
return translation.text
def perform_morphological_analysis(text):
tagger = MeCab.Tagger("")
result = tagger.parse(text)
return result
def main():
# Sample text in English
english_text = "Hello, how are you doing today?"
# Translate English to Japanese
japanese_translation = translate_text(english_text)
print("Translated Text:", japanese_translation)
# Perform morphological analysis on the Japanese text
analysis = perform_morphological_analysis(japanese_translation)
print("Morphological Analysis:\n", analysis)
if __name__ == "__main__":
main()
```
### Explanation
1. **Translation**: The `translate_text` function takes the English text and translates it into Japanese using the `googletrans` library.
2. **Morphological Analysis**: The `perform_morphological_analysis` function uses MeCab, a library for morphological analysis of Japanese text, to analyze the structure of the translated Japanese text.
3. **Output**: The program prints the translated text and its morphological analysis.
### Note
- **API Limitations**: The `googletrans` library is an unofficial client of Google Translate API. It might face stability issues or limitations if Google changes their internal APIs, so keep this in mind for production use.
- **MeCab Configuration**: MeCab works out-of-the-box for many users, but depending on your system, you might need to configure or install additional dictionaries for optimal performance.
This script provides a basic demonstration of translating text and performing morphological analysis. You can extend and modify it based on your specific requirements.英語のテキストを日本語に翻訳し、その翻訳されたテキストに対して形態素解析を行うPythonプログラムを作成する方法について説明します。googletrans(Google翻訳APIを使用する非公式ライブラリ)を翻訳に、mecab-python3を形態素解析に使用します。プログラムを設定する手順は以下の通りです。
前提条件
- Pythonのインストール: システムにPythonがインストールされていることを確認してください。
- パッケージのインストール: 必要なパッケージをインストールします。pipを使用してインストールできます。
pip install googletrans==4.0.0-rc1
pip install mecab-python3サンプルプログラム
以下は、英語のテキストを日本語に翻訳し、翻訳されたテキストに対して形態素解析を行うPythonスクリプトの例です:
from googletrans import Translator, LANGUAGES
import MeCab
def translate_text(text, dest='ja'):
translator = Translator()
translation = translator.translate(text, dest=dest)
return translation.text
def perform_morphological_analysis(text):
tagger = MeCab.Tagger("")
result = tagger.parse(text)
return result
def main():
# 英語のサンプルテキスト
english_text = "Hello, how are you doing today?"
# 英語を日本語に翻訳
japanese_translation = translate_text(english_text)
print("Translated Text:", japanese_translation)
# 日本語テキストの形態素解析を実行
analysis = perform_morphological_analysis(japanese_translation)
print("Morphological Analysis:\n", analysis)
if __name__ == "__main__":
main()説明
- 翻訳:
translate_text関数は英語のテキストを取り、googletransライブラリを使用して日本語に翻訳します。 - 形態素解析:
perform_morphological_analysis関数は、日本語テキストの構造を解析するために、形態素解析ライブラリであるMeCabを使用します。 - 出力: プログラムは翻訳されたテキストとその形態素解析を出力します。
注意
- APIの制限:
googletransライブラリはGoogle翻訳APIの非公式クライアントです。Googleが内部APIを変更すると安定性に問題が生じたり、制限がかかることがありますので、本番環境での使用には注意が必要です。 - MeCabの設定: MeCabは多くのユーザーにとってそのままで問題なく動作しますが、システムによっては最適なパフォーマンスを得るために追加の辞書を設定またはインストールする必要があります。
このスクリプトは、テキストの翻訳と形態素解析を行う基本的なデモンストレーションを提供します。特定の要件に基づいて拡張や修正が可能です。
こちらはJanomeではなくより一般的なMecabを使用した正しく動作するコードを生成しています。
このプロンプトに対する出力ではほとんど差は出ませんでしたが、GPT2はたった1行のプロンプトでゲームが作れてしまうほどの性能を有しています。
日本語能力
次に、GPT2は日本語能力も高いとのことでしたので、そちらも検証します。
以下のプロンプトを入力します。
ある企業が最近、新しい技術革新により市場での地位を強化しました。この技術は環境に優しい素材を使用しており、消費者からの関心も高いです。しかし、その企業は同時に労働者の権利に関する批判に直面しています。この状況を踏まえ、企業の評判を管理し、消費者の信頼を保つための戦略を提案してください。結果はこのようになりました。
企業が新しい技術革新により市場での地位を強化した一方で、労働者の権利に関する批判に直面しているという状況に対処するために、以下の戦略を提案します。
### 1. 状況分析
まず、企業は状況を正確に把握するために、内部と外部の両方で徹底的な調査を行う必要があります。
- **内部調査**: 労働者の権利に関連する問題点を明確にし、労働環境を改善するための具体的なステップを特定します。
- **外部調査**: 消費者、メディア、NGO、政府機関など、外部ステークホルダーの意見や懸念を把握します。
### 2. コンプライアンスと労働者の権利
労働者の権利に関する懸念に対応するために、以下の対策を実施します。
- **労働環境の改善**:
- 労働時間や賃金などの条件を見直し、適切な労働環境を確保する。
- 労働組合や従業員代表と協議し、労働者の声を反映させる。
- **コンプライアンスプログラムの強化**:
- 労働法規や国際規範に基づいた行動規範を制定し、全従業員に遵守させる。
- 定期的な監査を行い、問題が発見された場合は即座に是正する。
### 3. コミュニケーション戦略
労働者の権利に関する批判に対処し、新しい技術革新の利点を広めるためのコミュニケーション戦略を策定します。
- **透明性の確保**:
- 労働環境改善の取り組みやコンプライアンスプログラムの進捗状況を定期的に公開し、透明性を確保する。
- サステナビリティレポートやCSRレポートに詳細を記載する。
- **ポジティブな企業イメージの強化**:
- 新技術の環境への利点や、消費者にとってのメリットを強調するマーケティングキャンペーンを展開する。
- 技術革新の背景にある企業のビジョンや価値観を発信する。
- **ステークホルダーとの対話**:
- 労働者、消費者、NGO、政府機関、投資家などのステークホルダーと積極的に対話し、信頼を構築する。
- 意見交換の場を設け、指摘された問題に対して真摯に対応する。
### 4. 持続可能な企業方針の策定
企業の評判を長期的に向上させ、信頼を保つためには、持続可能な経営方針を策定する必要があります。
- **サステナビリティ戦略の制定**:
- 環境、社会、ガバナンス(ESG)に関する方針を明確にし、サステナビリティを経営の中核に据える。
- 労働者の権利、環境への配慮、社会貢献など、具体的な目標とアクションプランを設定する。
- **第三者認証の取得**:
- 労働者の権利やサステナビリティに関する第三者認証(例:ISO 14001、SA8000、B Corp)を取得し、信頼性を高める。
### 5. 危機管理とリスクマネジメント
批判に迅速かつ適切に対処するための危機管理体制を構築します。
- **危機対応チームの設置**:
- 労働問題や評判リスクに対処するための専任チームを設置する。
- メディア対応やステークホルダーへの説明責任を果たすための体制を整える。
- **リスクアセスメント**:
- 労働者の権利やサステナビリティに関する潜在的なリスクを定期的に評価し、事前に対策を講じる。
以上の戦略を実行することで、企業は評判を管理し、消費者の信頼を維持・向上させることができるでしょう。プロンプト内の複数の要素を完璧に理解し、それに対する非常に詳細な回答を出力してくれました。
詳細なだけでなく、非常に分かりやすくまとめられており、その能力の高さが伺えます。
ちなみに、たまたまgpt2-chatbotの対戦相手になったqwen-max-0428の回答がこちらです。
この状況において、企業が評判を管理し、消費者の信頼を維持するために取るべき戦略は以下の通りです。
1. **透明性とコミュニケーションの強化**: まず第一に、企業は労働者の権利に関する懸念に対して率直かつ迅速に対応する必要があります。正式な声明を発表し、具体的な改善策や取り組みを明確にすることが重要です。また、定期的に進捗状況を報告し、内外部のコミュニケーションチャネルを活用して、透明性を確保しましょう。
2. **労働条件の改善**: 批判を受け入れて、労働者の待遇や労働環境の改善に取り組む必要があります。適切な賃金、安全な作業場所、公正な人事評価制度、そしてワークライフバランスの尊重など、国際的な労働基準に従った施策を導入しましょう。労働組合との協力も重要です。
3. **持続可能なビジネスプラクティスの推進**: 環境に優しい素材を使用する技術革新は高く評価されていますが、これに加えて、全体的な持続可能性を追求することが求められます。サプライチェーンの責任、エネルギー効率、廃棄物削減などの取り組みを強化し、これらの成果を積極的に伝えることで、環境保護へのコミットメントをアピールします。
4. **社会的責任活動(CSR)の強化**: 労働者権利の問題を解決するだけでなく、地域社会やグローバルな社会課題に対する貢献も積極的に行いましょう。教育支援、貧困撲滅、災害支援などのCSR活動を通じて、企業の社会的役割を強調します。
5. **第三方評価機関による認証取得**: 国内外の信頼性のある機関から労働条件や環境管理システムについての認証を取得し、その結果を公表することで、改革の実績を客観的に証明します。これにより、消費者や投資家にとっての信頼性が向上します。
6. **顧客参与とフィードバックの循环**: 消費者からの意見や感想を受け入れ、改善に繋げる仕組みを構築します。オンライン調査、SNSでのコミュニケーション、フォーラムやワークショップの開催など、多様な方法で顧客との対話を促進します。
これらの戦略を総合力として展開することで、企業は技術革新の成果を活かしながら、労働者の権利問題を克服し、長期的な消費者信頼と市場でのリーダーシップを確立することができます。こちらも非常に有効な施策をいくつも上げてくれていますが、GPT2のほうがより詳細かつ理解しやすいものだと感じます。
数学能力
最後に、数学能力についても気になるため、実際に検証します。
以下の東京大学の理系数学入試問題を解かせてみます。
黒玉3個、赤玉4個、白玉5個が入っている袋から玉を1個ずつ取り出し、取り出した玉を順に横一列に12個並べる。ただし、袋から個々の玉が取り出される確率は等しいものとする。
(1) どの赤玉も隣り合わない確率pを求めよ。
この問題の正しい解答は、以下のようになっています。

国際数学オリンピックレベルの問題が解けるのであれば、この問題も難なく解けると思いますが結果はどうなるでしょうか。
上記の問題文を英訳して入力します。
Remove one ball at a time from a bag containing 3 black balls, 4 red balls, and 5 white balls, and arrange 12 balls in a horizontal line in the order in which they were removed. However, the probability that an individual ball is removed from the bag is assumed to be equal.
(1) Find the probability p that none of the red balls are adjacent to each other.結果はこのようになりました。
To solve the problem of finding the probability \( p \) that none of the 4 red balls are adjacent to each other after arranging all 12 balls in a horizontal line, we will follow these steps:
### Step 1: Understanding the Problem
We have a bag containing:
- 3 black balls (\( B \)),
- 4 red balls (\( R \)),
- 5 white balls (\( W \)).
We are to arrange all 12 balls in a horizontal line such that no two red balls are adjacent. This arrangement problem can be solved using the concept of permutations and combinatorial counting.
### Step 2: Finding the Total Arrangements
The total number of ways to arrange all 12 balls without any other constraints is given by:
\[ \frac{12!}{3! \times 4! \times 5!}, \]
where:
- \( 3! \) accounts for the indistinguishable black balls,
- \( 4! \) accounts for the indistinguishable red balls, and
- \( 5! \) accounts for the indistinguishable white balls.
Calculating this value:
\[ \frac{12!}{3! \times 4! \times 5!} = \frac{479001600}{6 \times 24 \times 120} = \frac{479001600}{17280} = 27720. \]
### Step 3: Finding the Favorable Arrangements
The favorable arrangements are those in which no two red balls are adjacent.
1. **Initial Arrangement of Black and White Balls:** First, arrange the 3 black balls and 5 white balls. There are 8 slots to arrange these balls:
\[ \frac{8!}{3! \times 5!} = \frac{40320}{6 \times 120} = \frac{40320}{720} = 56. \]
2. **Placing the Red Balls:** Now, we need to place the 4 red balls among the 9 gaps created between the black and white balls:
\[ \binom{9}{4} = 126. \]
3. **Total Favorable Arrangements:**
\[ 56 \times 126 = 7056. \]
### Step 4: Finding the Probability
The probability \( p \) that no two red balls are adjacent is:
\[ p = \frac{7056}{27720} = \frac{294}{1155} = \frac{98}{385} = \frac{14}{55}. \]
Therefore, the probability that none of the red balls are adjacent to each other is:
\[ \boxed{\frac{14}{55}}. \]12 個のボールをすべて横一列に配置した後、4 つの赤いボールがどれも隣接しない確率 ( p ) を求める問題を解決するには、次の手順に従います。
ステップ 1: 問題を理解する
以下のものが入ったバッグがあります。
- 黒いボール 3 個 (( B ))、
- 赤いボール 4 個 (( R ))、
- 白いボール 5 個 (( W ))。
2 つの赤いボールが隣接しないように、12 個のボールすべてを横一列に配置します。 この配置の問題は、順列と組み合わせ計数の概念を使用して解決できます。
ステップ 2: 全体の配置を見つける
他の制約なしで 12 個のボールすべてを配置する方法の総数は、次の式で求められます。
[ \frac{12!}{3! \4 倍! \5 倍!}、]
どこ:
- ( 3! ) は区別できない黒いボールを表します。
- ( 4! ) は区別できない赤いボールを表し、
- ( 5! ) は、区別できない白いボールを表します。
この値を計算すると、次のようになります。
[ \frac{12!}{3! \4 倍! \times 5!} = \frac{479001600}{6 \times 24 \times 120} = \frac{479001600}{17280} = 27720. ]
ステップ 3: 有利な取り決めを見つける
好ましい配置は、2 つの赤いボールが隣接しない配置です。
- 白と黒のボールの初期配置: まず、3 つの黒ボールと 5 つの白ボールを配置します。 これらのボールを配置するには 8 つのスロットがあります。
[ \frac{8!}{3! \times 5!} = \frac{40320}{6 \times 120} = \frac{40320}{720} = 56. ] - 赤いボールの配置: 次に、黒と白のボールの間に作成された 9 つの隙間に 4 つの赤いボールを配置する必要があります。
[ \binom{9}{4} = 126. ] - 全体的に有利な取り決め:
[ 56 \times 126 = 7056. ]
ステップ 4: 確率を求める
2 つの赤いボールが隣接しない確率 ( p ) は次のとおりです。
[ p = \frac{7056}{27720} = \frac{294}{1155} = \frac{98}{385} = \frac{14}{55}。 ]
したがって、どの赤いボールも互いに隣接しない確率は次のようになります。
[ \boxed{\frac{14}{55}}。 ]
少し見にくいですが、正解です!
この問題は、Gemini UltraやClaude 3などの最新モデルでも正解できなかった問題なので、非常に高い計算能力を有していることが伺えます。
このように、非常に高性能なGPT2が再び使用可能になったので、もし気になる方は是非試してみてください!
今後も新たな情報が判明次第アップデートしていきます。

生成系AIの業務活用なら!
・生成系AIを活用したPoC開発
・生成系AIのコンサルティング
・システム間API連携
最後に
いかがだったでしょうか?
GPT-3.5 Turboの最新アップデートで、より高速かつ低コストでのAI活用が可能になりました。自社での導入・活用を検討する際に、最適なモデル選定や活用方法について、一緒に考えてみませんか?
弊社では
・マーケティングやエンジニアリングなどの専門知識を学習させたAI社員の開発
・要件定義・業務フロー作成を80%自動化できる自律型AIエージェントの開発
・生成AIとRPAを組み合わせた業務自動化ツールの開発
・社内人事業務を99%自動化できるAIツールの開発
・ハルシネーション対策AIツールの開発
・自社専用のAIチャットボットの開発
などの開発実績がございます。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、サービス紹介資料もご用意しておりますので、併せてご確認ください。




