Phi-4-miniは何がすごい?Microsoftの軽量モデル試してみた!概要・使い方・料金まで解説

- 小型ながらに大規模言語モデルに匹敵する性能
- メモリ消費を削減しつつ、処理は高速化
- Function Callingが使えるため外部APIやプログラムインターフェースの連携がスムーズ
2025年2月27日、Microsoftから新たなLLMが登場!
今回リリースされたモデルはPhi-4-miniとPhi-4-multimodal。Phi-4-miniは3.8億パラメータを持つコンパクトなモデルです。コンパクトなモデルではありながらも、従来の大型モデルに匹敵する性能を発揮しています。
本記事では、Phi-4-miniの概要や従来のPhi-4との違い、Phi-4-miniの実装方法についてお伝えします。本記事を最後までお読みいただければ、Phi-4-miniの理解が深まります。
ぜひ最後までお読みください!
\生成AIを活用して業務プロセスを自動化/
Phi-4-miniの概要
Phi-4-miniはMicrosoftが新たにリリースをしたSLMです。従来のモデルに比べて小型のモデルでありながら、同等の性能を発揮します。
Phi-4-miniは高速かつ高精度なテキスト処理を行うために、開発されており、特に推論や数学タスク、コーディングなどの分野で優れた性能を発揮。
また小型かつ高速なモデル設計のため、エッジデバイスやオンデバイス実行での利用が可能になりました。
Phi-4-miniの特徴
Phi-4-miniは小型かつ高速な処理を実現するために、Grouped-Query Attention (GQA)を採用しています。GQAを採用することで、従来に比べメモリ消費を1/3に削減。また、長文生成時のKVキャッシュの効率化を実現。
Phi-4-miniは128,000トークンまでの長文シーケンスに対応しており、数学の証明や長文生成、コード生成などに最適と言えます。
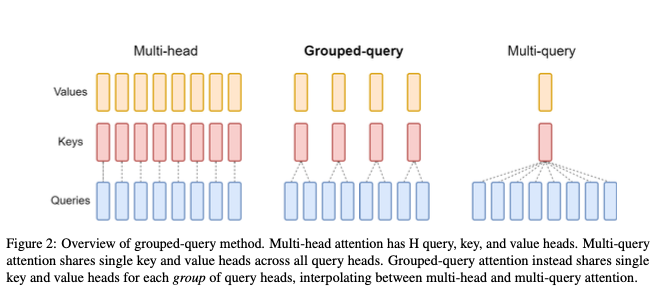
Grouped-Query Attention
Grouped-Query Attentionとは、Transformerモデルの推論速度を向上させるための手法です。Chat GPTなどの大規模言語モデルでは、Transformerが活用されていますが、TransformerにはMulti-Head Attentionという手法が採用されています。
しかし、Multi-Head Attentionはdecoderの重みとすべてのアテンションのキーとバリューをロードするため、メモリ帯域幅のオーバーヘッドが大きいという課題がありました。
そこで、オーバーヘッドを解決するために考えられたのがMulti-Query Attentionです。Multi-Query AttentionはMulti-Head Attentionに比べると高速化されていますが、品質劣化を招く可能性があります。
そして、Multi-Query AttentionとMulti-Head Attentionのいいとこ取りをした手法であるGrouped-Query Attentionが考えられました。Grouped-Query AttentionはMulti-Head Attentionと同等の品質を保ちつつ、Multi-Query Attentionの速度を実現しています。
KVキャッシュ
KVキャッシュとは、キーバリューキャッシュのことで、LLMの推論プロセスにおけるメモリ効率と速度の最適化のために使われる技術です。
メモリ効率のために使われるのにメモリ消費量が増えるという、一見矛盾する特徴があります。
しかし、Phi-4-miniではメモリ消費を1/3に削減することができているため、KVキャッシュのデメリットであるメモリ消費量はあまり大きな問題にはならず、推論速度が向上します。
Phi-4-miniの性能
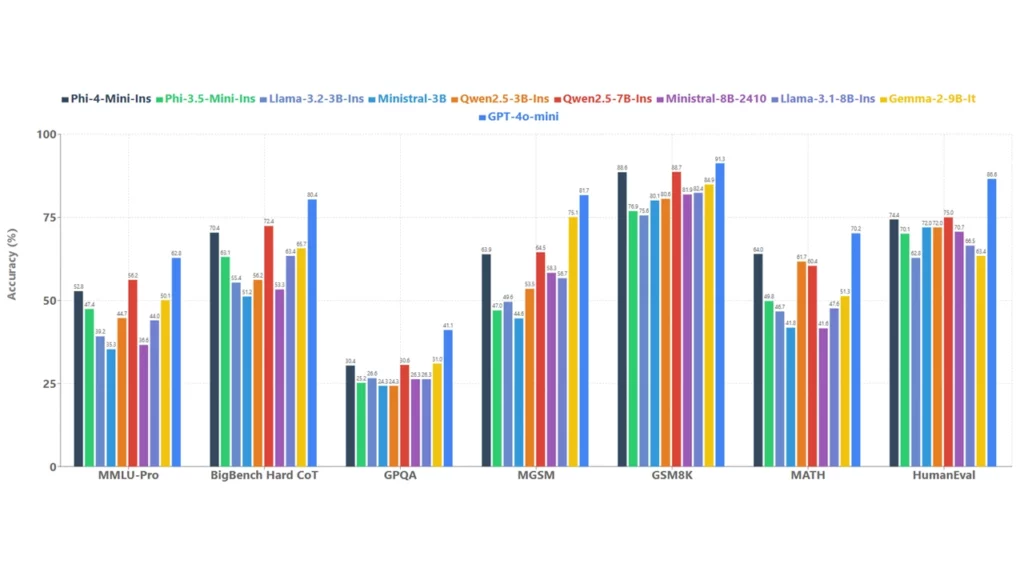
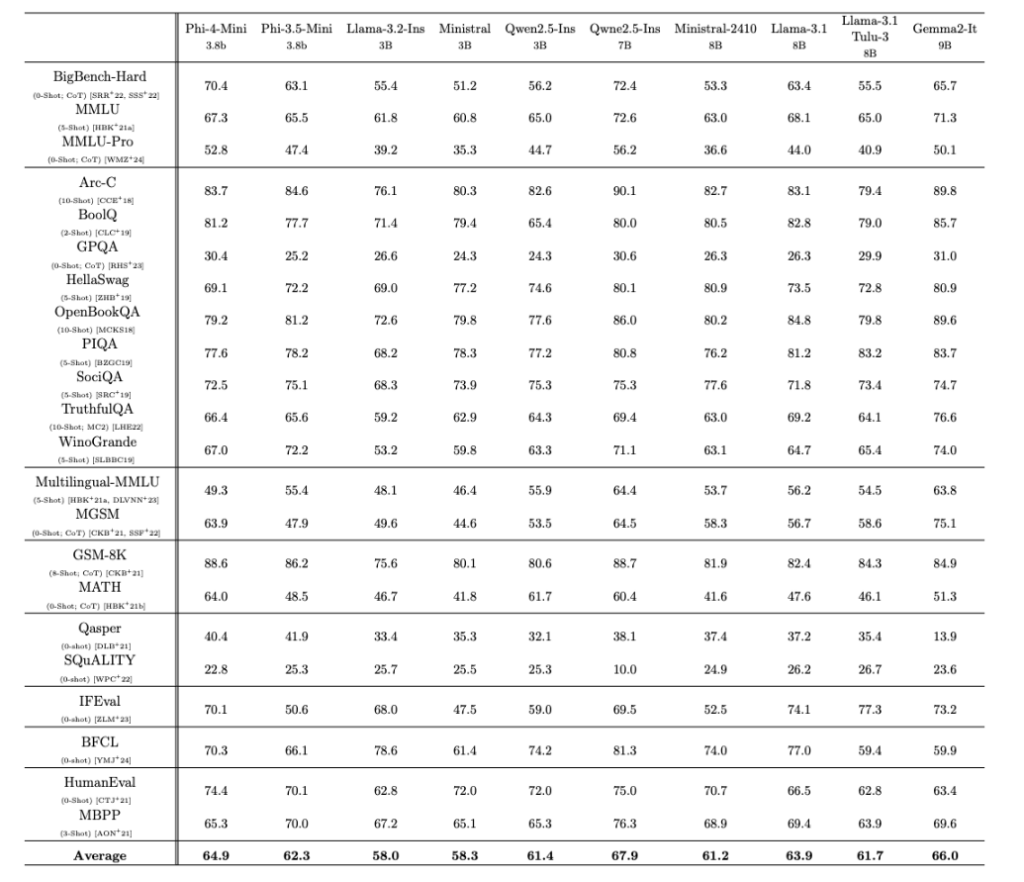
Microsoftが発表したパフォーマンスでは、GSM8KとBigBench Hard CoTで高い性能を発揮。それぞれLlama-3.1-8B-InsとQwen2.5-7B-Insに匹敵します。
また、GPQAではLlama-3.2-3B-InsやMistral-3B を上回ります。HumanEvalではGPT-4o-miniには劣りますが、それでも70.2% のスコアをとっており、コーディング能力の高さも伺えます。
また、アベレージで見ると上位3位に組み込む性能であり、小型ながらに性能の高さがわかります。
さらにPhi-4-miniではFunction Calling(関数呼び出し)を行うこともでき、外部APIやプログラムインターフェースと連携が可能です。
Phi-4-miniとPhi-4の違い
2024年12月にPhi-4がリリースされていますが、わずか2ヶ月で新たなモデルのリリースです。
Phi-4-miniとPhi-4の違いはどこにあるのでしょうか?
まず第一にminiというだけあり、パラメータ数は3.8Bと14Bで異なります。その一方でPhi-4-miniは小型ながらにテキストベースの推論やコーディングに特化しています。
Phi-4は推論と数学タスクに特化しており、その性能はGPT-4oを上回る性能です。そのため、Phi-4-miniは軽量・高速推論に、Phi-4は高度な数学・推論タスクといった具合に使い分けるのが良いでしょう。
また、トレーニング方法にも違いがあります。Phi-4-miniはWebデータと合成データを使って効率的な学習を行い、合成Chain-of-Thought (CoT) データを導入し、推論能力を強化しています。
それに対してPhi-4は、事前トレーニング・中間トレーニング・事後トレーニングと段階を踏んでトレーニングを行い、ピボタルトークン検索を用いてDPOデータペアの効率的な生成を実施しています。
Phi-4-miniのライセンス
Phi-4-miniのライセンスはMITライセンスです。商用利用や改変なども可能ですが、配布する場合には、元の著作権表示とライセンスの全文を記載する必要があるので注意しましょう。
| 利用用途 | 可否 |
|---|---|
| 商用利用 | ⭕️ |
| 改変 | ⭕️ |
| 配布 | ⭕️ |
| 特許使用 | ⭕️ |
| 私的使用 | ⭕️ |
なお、検閲を回避し、正確な回答を実現するPerplexityのR1-1776について詳しく知りたい方は、下記の記事を合わせてご確認ください。
Phi-4-miniの使い方
Phi-4-miniは次のいずれかで使うことができます。
今回はHugging Faceの情報からgoogle colaboratoryで実装してみます。
◼︎システム RAM
4.0/ 83.5 GB
◼︎GPU RAM
7.7 / 40.0 GB
◼︎ディスク
46.7 / 235.7 GB
◼︎GPUの種類:A100
◼︎プラン:有料
まずは必要ライブラリのインストールです。
!pip install torch transformers accelerate flash-attn次にモデルのダウンロードです。
モデルのダウンロードはこちら
import torch
from transformers import AutoModelForCausalLM, AutoTokenizer
model_path = "microsoft/Phi-4-mini-instruct"
tokenizer = AutoTokenizer.from_pretrained(model_path)
model = AutoModelForCausalLM.from_pretrained(
model_path,
device_map="auto",
torch_dtype=torch.float16,
trust_remote_code=True
).to("cuda") # GPUを使用サンプルコードはこちら
from transformers import pipeline
# パイプラインの作成
pipe = pipeline(
"text-generation",
model=model,
tokenizer=tokenizer,
)
# プロンプトの設定
prompt = "Explain the importance of mathematics in machine learning."
# 生成の設定
generation_args = {
"max_new_tokens": 300,
"return_full_text": False,
"temperature": 0.7,
"do_sample": True,
}
# テキスト生成
output = pipe(prompt, **generation_args)
print(output[0]['generated_text'])
結果はこちら
Mathematics plays a crucial role in machine learning, providing the foundation for algorithms, models, and concepts that are essential for developing intelligent systems. Here are some key aspects of the importance of mathematics in machine learning:
1. **Algorithm Development**: Many machine learning algorithms are based on mathematical principles. For example, linear regression relies on least squares estimation, k-nearest neighbors (k-NN) uses distance metrics like Euclidean distance, and decision trees involve recursive partitioning based on entropy and information gain. These algorithms are mathematically defined and rely on mathematical optimization to find the best solution.
2. **Modeling Relationships**: Mathematics allows us to model relationships between variables and features. Linear algebra, for instance, is used to understand and manipulate high-dimensional data, while calculus helps in understanding the gradients and optimization techniques used in training models, such as gradient descent.
3. **Optimization**: Machine learning models often need to be trained, which involves minimizing or maximizing a loss function. Techniques like gradient descent, Newton's method, and others are based on calculus and provide a way to iteratively improve the model's parameters. Additionally, convex optimization plays a significant role in ensuring that the solution found is a global minimum.
4. **Probability and Statistics**: Probability theory and statistics are central to machine learning. They provide the tools to handle uncertainty, make inferences, and understand the distribution of data. Concepts like hypothesis testing, Bayesian inference, and information theory are used to design statistical tests, build probabil日本語訳はこちら
数学は機械学習において重要な役割を果たし、インテリジェント システムの開発に不可欠なアルゴリズム、モデル、概念の基盤を提供します。機械学習における数学の重要性の主な側面は次のとおりです。
1. **アルゴリズム開発**: 多くの機械学習アルゴリズムは数学的原理に基づいています。たとえば、線形回帰は最小二乗推定に依存し、k 近傍法 (k-NN) はユークリッド距離などの距離メトリックを使用し、決定木はエントロピーと情報ゲインに基づく再帰分割を伴います。これらのアルゴリズムは数学的に定義され、最適なソリューションを見つけるために数学的最適化に依存しています。
2. **関係のモデリング**: 数学を使用すると、変数と機能の関係をモデル化できます。たとえば、線形代数は高次元データを理解および操作するために使用され、微積分は勾配降下法などのトレーニング モデルで使用される勾配と最適化手法を理解するのに役立ちます。
3. **最適化**: 機械学習モデルは、損失関数を最小化または最大化するトレーニングが必要になることがよくあります。勾配降下法、ニュートン法などの手法は微積分に基づいており、モデルのパラメータを反復的に改善する方法を提供します。さらに、凸最適化は、見つかったソリューションがグローバル最小値であることを保証する上で重要な役割を果たします。
4. **確率と統計**: 確率理論と統計は機械学習の中心です。これらは、不確実性を処理し、推論を行い、データの分布を理解するためのツールを提供します。仮説検定、ベイズ推論、情報理論などの概念は、統計テストの設計、確率の構築に使用されます。サンプルコードを実行して、もしエラーになった場合は、下記を追加で実行してください。各種ライブラリのバージョンでエラーが起こったりします。
!pip install torch==2.6.0+cu124 torchvision==0.21.0+cu124 torchaudio==2.6.0+cu124 --index-url https://download.pytorch.org/whl/cu124
!pip install transformers==4.49.0 flash-attn==2.7.4.post1結果を見てみると、適切に回答できているように思います。
Phi-4-miniの性能をGemini 2.0 pro Experimentalと比較検証
Phi-4-miniは小型ながらにテキストベースの推論や数学タスク、コーディングを得意としているので、Gemini 2.0 pro Experimentalに同じタスクを行わせ、どのような結果になるかを検証してみたいと思います。
実施するタスクとしては次の3つです。
- Aさん、Bさん、Cさんのうち、Aさんは正直者、Bさんは嘘つき、Cさんはどちらでもある。Aさんは『Bさんは嘘をついている』と言った。Cさんは誰の味方か?
- 偶数と偶数を足すと必ず偶数になることを証明せよ。
- forループの使い方を説明するサンプルコードを書いてください。
タスク1ではテキストベースの推論として前後関係の理解や仮定の推論、タスク2では数学能力、タスク3ではコーディング能力を見ていきたいと思います。
タスク1.テキストベースの推論
モデルのダウンロードまでは一緒なので割愛し、実行するコードと結果を提示します。
サンプルコードはこちら
from transformers import pipeline
pipe = pipeline(
"text-generation",
model=model,
tokenizer=tokenizer,
)
prompt = "Aさん、Bさん、Cさんのうち、Aさんは正直者、Bさんは嘘つき、Cさんはどちらでもある。Aさんは『Bさんは嘘をついている』と言った。Cさんは誰の味方か?"
generation_args = {
"max_new_tokens": 300,
"return_full_text": False,
"temperature": 0.7,
"do_sample": True,
}
output = pipe(prompt, **generation_args)
print(output[0]['generated_text'])Phi-4-miniの結果はこちら
答え:Bさん。理由:Aさんは正直者であるため、彼はBさんが嘘つきであることを正しく言っている。Cさんはどちらでもあるため、AさんとBさんのどちらの味方でもなく、むしろ両方の側面を持っている可能性があるため、誰かの味方ではない。したがって、Cさんは誰の味方でもない。Gemini 2.0 pro Experimentalの結果はこちら
この問題は論理パズルですね。Aさんの発言と、それぞれの人物の特性からCさんの立場を推理します。
Aさんの発言の分析: Aさんは正直者なので、Aさんの発言「Bさんは嘘をついている」は真実です。
Bさんの特性: Aさんの発言が真実であることから、Bさんは嘘つきであることが確定します。
Cさんの立場:
Cさんは「正直者」の場合と「嘘つき」の場合、どちらもありえます。
しかし、この問題の状況下では、Bさんが嘘つきであることは確定しています。
よってAさんの発言は真実であり、Cさんは、Aさんの味方であるといえます。
結論: CさんはAさんの味方です。早速結果が分かれました。
「Cさんは誰の味方か?」という問いに対して、Phi-4-miniでは最初にBさんと答えていますが、最後にCさんは誰の味方でもない、と答えています。
Gemini 2.0 pro ExperimentalではCさんはAさんの味方と言っています。これが正しいですね。Aさんが正しいことを言っているのに、CさんがBさんの味方をしてしまうと、Aさんが嘘をついていることになり、矛盾してしまいます。
タスク2.数学タスク
次は数学タスクとして「偶数と偶数を足すと必ず偶数になることを証明せよ。」という指示を与えます。
サンプルコードはこちら
from transformers import pipeline
pipe = pipeline(
"text-generation",
model=model,
tokenizer=tokenizer,
)
prompt = "偶数と偶数を足すと必ず偶数になることを証明せよ。"
generation_args = {
"max_new_tokens": 300,
"return_full_text": False,
"temperature": 0.7,
"do_sample": True,
}
output = pipe(prompt, **generation_args)
print(output[0]['generated_text'])Phi-4-miniの結果はこちら
次の証明を与えよう: x は偶数であり、y は偶数であると仮定します。例えば、x = 2k および y = 2m であるとしましょう。ここで k と m は整数です。x + y = 2k + 2m = 2(k + m) です。k + m は整数であるため、偶数 2(k + m) です。したがって、x + y は偶数です。したがって、偶数と偶数の和は常に偶数です。Gemini 2.0 pro Experimentalの結果はこちら
証明は以下のようになります。
証明
偶数の定義: 任意の整数 n に対して、2n と表せる数を偶数と定義します。
2つの偶数を設定: 2つの異なる偶数を考えます。これらを 2m および 2k と表します(m と k は任意の整数)。
2つの偶数の和: これらの偶数の和は、2m + 2k となります。
式変形: この式は、分配法則を用いて 2(m + k) と変形できます。
結論: m と k は整数なので、m + k も整数です。したがって、2(m + k) は、ある整数(m + k)の2倍であり、偶数の定義に合致します。
以上より、偶数と偶数を足すと必ず偶数になることが証明されました。今回はどちらも正解を導けています。ただ、理解しやすい結果出力はGemini 2.0 pro Experimentalかなと感じます。
タスク3.コーディング能力
最後にコーディング能力を検証するために「forループの使い方を説明するサンプルコードを書いてください。」という指示を与えます。
サンプルコードはこちら
from transformers import pipeline
pipe = pipeline(
"text-generation",
model=model,
tokenizer=tokenizer,
)
prompt = "forループの使い方を説明するサンプルコードを書いてください。"
generation_args = {
"max_new_tokens": 300,
"return_full_text": False,
"temperature": 0.7,
"do_sample": True,
}
output = pipe(prompt, **generation_args)
print(output[0]['generated_text'])Phi-4-miniの結果はこちら
ループを使って、`my_list`という名前のリストの各要素を繰り返し印刷してください。Pythonのforループを使用して、`my_list`というリストの各要素を繰り返し印刷するには、インデックスを使用していない簡単なforループが使用できます。以下がサンプルコードです:
```python
my_list = [1, 2, 3, 4, 5] # ここであなたのリストを定義します
for element in my_list:
print(element)
```
このコードは、`my_list`の各要素をターゲットとして繰り返し処理し、その値を出力します。Gemini 2.0 pro Experimentalの結果はこちら
# 例1: リストの要素を順番に出力する
fruits = ["apple", "banana", "cherry"]
for fruit in fruits:
print(fruit)
# 例2: range()関数を使って、指定回数だけ処理を繰り返す
for i in range(5): # 0から4までの整数を順番に生成
print(f"Iteration number: {i}")
# 例3: 文字列の各文字を順番に出力する
message = "Hello"
for char in message:
print(char)
# 例4: enumerate()関数を使って、インデックスと要素を同時に取得する
for index, fruit in enumerate(fruits):
print(f"Fruit at index {index}: {fruit}")
# 例5: 入れ子(ネスト)のforループ (九九の表を出力)
for i in range(1, 10):
for j in range(1, 10):
print(f"{i} x {j} = {i*j}", end="\t") # タブ区切りで出力
print() # 各段の後に改行
# 例6: break文を使ってループを途中で抜ける
numbers = [1, 2, 3, 4, 5]
for number in numbers:
if number == 3:
break # numberが3になったらループを抜ける
print(number)
# 例7: continue文を使って、現在のイテレーションをスキップする
for number in numbers:
if number == 3:
continue # numberが3のときは以下の処理をスキップ
print(number)
# 例8: 辞書(dictionary)のキーと値をループで処理する
person = {"name": "Alice", "age": 30, "city": "New York"}
# キーのみを取得
for key in person:
print(key)
# 値のみを取得 (person.values() を使う)
for value in person.values():
print(value)
# キーと値の両方を取得 (person.items() を使う)
for key, value in person.items():
print(f"{key}: {value}")
# 例9: リスト内包表記 (list comprehension) ※forループの応用
# 0から9までの整数の2乗のリストを生成
squares = [x**2 for x in range(10)]
print(squares)
# 例10: リスト内包表記 (条件付き)
# 0から9までの整数のうち、偶数のみのリストを生成
even_numbers = [x for x in range(10) if x % 2 == 0]
print(even_numbers)
content_copy
download
Use code with caution.
Python
各コードの説明
例1: 最も基本的な for ループ。リストの要素を一つずつ取り出して処理します。
例2: range() 関数と組み合わせて、指定した回数だけループします。range(n) は 0 から n-1 までの整数を生成します。
例3: 文字列もイテラブル(反復可能)オブジェクトなので、for ループで各文字を処理できます。
例4: enumerate() 関数を使うと、要素のインデックスと値を同時に取得できます。
例5: for ループをネスト(入れ子)にして、より複雑な処理を行います(九九の表)。
例6: break 文を使うと、特定の条件が満たされたときにループを強制的に終了できます。
例7: continue 文を使うと、現在のイテレーション(繰り返し)をスキップして、次のイテレーションに進みます。
例8: 辞書 (dictionary) を for ループで処理する様々な方法を示しています。
for key in person:: キーを順番に取得
for value in person.values():: 値を順番に取得
for key, value in person.items():: キーと値のペアを順番に取得
例9: リスト内包表記 (list comprehension)。for ループをより簡潔に記述し、新しいリストを生成する強力な方法です。
例10: リスト内包表記に条件(if)を追加した例。
これらの例は、for ループのさまざまな使い方を網羅しています。 状況に応じて適切な方法を選択することが重要です。 forループはPythonプログラミングの基本中の基本なので、しっかりと理解しておきましょう。今回もどちらも適切な回答を出力してくれました。トークンの関係もあってPhi-4-miniの出力量が少ないですが、これだけでみるとGemini 2.0 pro Experimentalが非常に丁寧な回答という印象を持ちますね。
また、与えた指示の背景も汲み取ってくれていそうな感じがします。「forループの使い方を説明するサンプルコードを書いてください。」という指示は、プログラミング初心者が与えそうな指示ですが、Gemini 2.0 pro Experimentalは詳細に解説をしてくれています。
今回の結果からは、Phi-4-miniは文脈の前後関係や論理的な推論を苦手とするものの、コーディングや数学タスクは一定の性能で出力できそうであることがわかりました。
なお、スマホで動くMicrosoftのPhi 3.5について詳しく知りたい方は、下記の記事を合わせてご確認ください。

まとめ
本記事では、Phi-4-miniの概要や従来のPhi-4との違い、Phi-4-miniの実装方法についてお伝えをしました。Phi-4-miniは小型かつ高速処理が可能なため、エッジデバイスやスマートデバイスに組み込み、音声アシスタントやスマートホーム制御、組み込みAIシステムなどで活用ができそうですね。
ぜひ本記事を参考にPhi-4-miniを実装してみてください。
弊社では、Phi 3.5を活用したローカル環境でのデータ分析システムを開発しました。事例について詳しく知りたい方は以下の記事をご覧ください。

最後に
いかがだったでしょうか
Phi-4-miniのコンパクトな設計と高性能な処理は、エッジデバイスでの活用や既存システムとのAPI連携を強化することが可能です。既存システムとの連携を最適化し、業務の自動化・高度化を推進できます。
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、大規模言語モデル(LLM)を対象に、言語理解能力、生成能力、応答速度の各側面について比較・検証した資料も配布しております。この機会にぜひご活用ください。







