視覚推論ができるQVQ-72B-PreviewをAlibabaが公開!実装方法と性能を解説

- 視覚推論機能に重点を置いたモデル
- 段階的推論で問題を解き進める
- 複雑な図形問題や幾何学の確率計算など、視覚情報を必要とするタスクに対応可能
2024年12月25日、Alibabaから新たな視覚推論モデルがリリースされました。
新たな視覚推論モデルである「QVQ」は、視覚推論機能の強化に重点が置かれた実験的な研究モデル。従来のQwen2-VL 72Bモデルの性能を大幅に上回っています。特に、視覚情報を用いる数学の問題で、高いパフォーマンスを発揮します。
本記事ではQVQの概要から実装方法をお伝えし、性能について検証してみたいと思います。ぜひ最後までお読みください!
\生成AIを活用して業務プロセスを自動化/
QVQ-72B-Previewの概要
Alibabaが新たにリリースしたQVQ-72B-Previewは、視覚情報と高度な推論能力を兼ね備えたマルチモーダルモデルです。
このモデルは言語モデルとして、ユーザーからの複雑な文章や質問を理解し、それに基づいて回答生成する能力を持っています。特に、数学の問題や科学的な説明など、テキスト形式で記述された情報を論理的に理解することが可能です。
また、ユーザーから入力されたテキストのみを理解するのではなく、添付された画像からも情報を理解。例えば、幾何学の問題において、図形の関係性や座標を正確に認識し、計算や推論に活用します。
入力されたテキスト・添付された画像情報をひとまとめにして、段階的に推論を行うため、視覚情報を活用した数学や科学分野で特に優れたパフォーマンスを発揮します。
段階的推論(Step-by-step reasoning)
段階的推論は、複雑な問題を解決する際に、解決過程を複数の小さなステップに分割して進める推論方法です。QVQ-72B-Previewでは、この段階的推論を活用し、テキスト情報と画像などの視覚情報を論理的に分解しながら問題解決を進めます。
これは、視覚情報を推論に活用できるモデルだからこそ実現可能な技術。視覚推論機能の強化に重点を置いており、画像などテキスト以外のデータ処理を得意としています。
その結果、QVQ-72B-Previewで使用される段階的推論は、問題解決の過程を透明で正確にするための重要な技術となっています。
多段階推論(Multi-step reasoning)との違い
段階的推論に似た推論方法に多段階推論(Multi-step reasoning)があります。
多段階推論も問題解決を複数のステップに分割して解決していきますが、主な焦点は最終的な回答を得ることです。各段階での進行は、全体的な戦略の一部として設計され、ステップ間の連続性が重視されます。
一方で、段階的推論では、問題解決を一連の小さなステップに分解しますが、各ステップの論理的整合性と透明性が主な焦点です。各ステップが独立して正確である必要があり、エラーが発生した場合でもその原因を追跡・修正しやすい構造になっています。
それぞれの違いを簡単にまとめると以下の表のようになります。
| 特徴 | 多段階推論 | 段階的推論 |
|---|---|---|
| 目的 | 最終的な回答の達成 | 各ステップの正確性と透明性 |
| ステップ間の依存性 | 高い | 低い |
| エラー管理 | エラーが伝播しやすい | エラーを各ステップで修正可能 |
| 応用分野 | 大規模で複雑な連鎖推論 | 細かな検証が必要な論理解析 |
QVQ-72B-Previewと従来モデルの違い
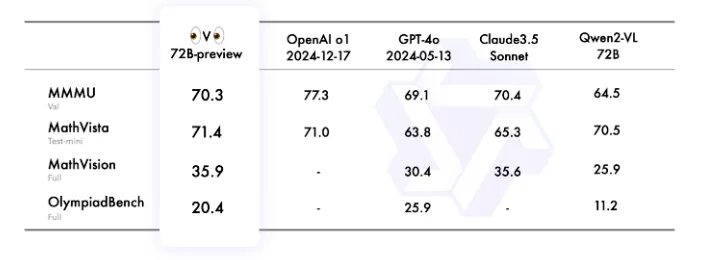
QVQ-72B-Previewの視覚的推論能力は、既存モデルであるQwen2-VL-72B-Instructと比較して、特に数学や科学の問題において大幅に向上。特に以下の3つの点で性能が向上しています。
- MMMUベンチマークでのスコア
- MMMUで70.3という高いスコアを達成しており、これはQwen2-VL-72B-Instructを大幅に上回る。
- 数学関連ベンチマークでの改善
- MathVistaやMathVisionなどの数学関連ベンチマークでも、著しく性能が向上。
- OlympiadBenchでの性能
- OlympiadBenchにおいても、難しい問題への対応能力が向上しており、特に数学や物理の分野で優れた結果。
これらの結果から、単に画像認識だけでなく、画像の内容を理解し、それに基づいて論理的な推論を行う能力が、既存モデルよりも大幅に向上していることがわかります。特に、数学や科学などの分野で、複雑な問題をステップごとに解決していく能力が高いことが特徴ですね。
QVQ-72B-Previewの限界
公式ページでは、限界について述べられています。
- 言語の混合とコード切り替え
- モデルは言語を混合したり、予期せず言語を切り替えたりして、応答の明瞭性に影響を与える可能性ある。
- 再帰的推論
- モデルは循環的な論理パターンに陥り、結論に達することなく冗長な応答を生成する可能性がある。
- 安全性と倫理的考慮事項
- このモデルでは、信頼性とセキュリティの高いパフォーマンスを確保するために強化された安全対策が必要であり、ユーザーはモデルを導入する際に注意する必要がある。
- パフォーマンスとベンチマークの制限
- モデルは視覚的推論において改善が見られましたが、Qwen2-VL-72B-Instructの機能を完全に置き換えることはできません。さらに、複数ステップの視覚的推論中に、モデルは徐々に画像コンテンツへの焦点を失い、幻覚を引き起こす可能性がある。
実際にQVQ-72B-Previewを使う場合には、上記4つの限界点をしっかり理解した上で使用するようにしましょう!
QVQ-72B-Previewのライセンス
ライセンスはQwen LICENSEです。以下の利用用途全てが可能ですが、商用利用と特許使用のみ条件があります。
- 商用利用:月間アクティブユーザー(MAU)が1億人を超える場合は、Alibaba Cloudにライセンスを申請し、許可を得る必要がある。
- 特許使用:ライセンス契約内に特許利用に関する直接的な言及はありません。ただし、特許関連の紛争が発生した場合、契約に基づくライセンスが終了する旨が記載されています。
| 利用用途 | 可否 |
|---|---|
| 商用利用 | ⭕️(条件あり) |
| 改変 | ⭕️ |
| 配布 | ⭕️ |
| 特許使用 | ⭕️(条件あり) |
| 私的使用 | ⭕️ |
なお、より高度な推論タスクにも対応しているアリババ発のAI「Marco-o1」について詳しく知りたい方は、下記の記事を合わせてご確認ください。

QVQ-72B-Previewの使い方
72Bなので、google colaboratoryでの実行は難しいです。もし実行する場合にはVast.aiなどのクラウドGPUを借りて実装するのが良いでしょう。
また、Hugging FaceのSpacesでQVQ-72B-Previewが用意されているので、こちらから使うこともできます。
プレビュー版で、積分の問題を解かせてみました。
非常に長い回答を滞りなく回答してくれました。同じ問題をGPT-4oにも投げかけてみると、
特殊文字を正しく表示するためのエンコード( ​)がそのまま表示されて表示されてしまい、回答が適切に表示されませんでした。
Vast.aiを使ったQVQ-72B-Previewの実装方法
Vast.aiを使って実装しようと思いましたが、80GBのGPUメモリでも不足してしまいました。もっと大きいメモリがないと動きませんが、やり方の手順は載せておきます。
まずは必要ライブラリをインストールしましょう。
!sudo apt update && sudo apt upgrade -y
!sudo apt install python3-pip git -y
!pip install torch torchvision transformers
!pip install qwen-vl-utilsモデルのダウンロードはこちら
# device_mapを使用せずにモデルを読み込む
model = Qwen2VLForConditionalGeneration.from_pretrained(
"Qwen/QVQ-72B-Preview",
torch_dtype=torch.bfloat16, # メモリ使用量を削減
low_cpu_mem_usage=False
)
if torch.cuda.is_available():
model = model.to("cuda")
processor = AutoProcessor.from_pretrained("Qwen/QVQ-72B-Preview")サンプルコードの実行はこちら
def process_image(image_path, question):
# Prepare messages
messages = [
{
"role": "system",
"content": [
{"type": "text", "text": "You are a helpful and harmless assistant."}
],
},
{
"role": "user",
"content": [
{
"type": "image",
"image": image_path
},
{"type": "text", "text": question}
],
}
]
# Prepare inputs
text = processor.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
image_inputs, video_inputs = process_vision_info(messages)
inputs = processor(
text=[text],
images=image_inputs,
videos=video_inputs,
padding=True,
return_tensors="pt"
)
inputs = inputs.to("cuda")
# Generate response
generated_ids = model.generate(**inputs, max_new_tokens=8192)
generated_ids_trimmed = [
out_ids[len(in_ids):] for in_ids, out_ids in zip(inputs.input_ids, generated_ids)
]
output_text = processor.batch_decode(
generated_ids_trimmed,
skip_special_tokens=True,
clean_up_tokenization_spaces=True
)
return output_text[0]
# Example usage
if __name__ == "__main__":
image_path = "Math_2.jpg"
question = "Evaluate the integral of the functions graphed using the formula for circles:"
response = process_image(image_path, question)
print(response)結果はこちら
ile /opt/conda/lib/python3.11/site-packages/torch/nn/modules/module.py:1736, in Module._wrapped_call_impl(self, *args, **kwargs)
1734 return self._compiled_call_impl(*args, **kwargs) # type: ignore[misc]
1735 else:
-> 1736 return self._call_impl(*args, **kwargs)
File /opt/conda/lib/python3.11/site-packages/torch/nn/modules/module.py:1747, in Module._call_impl(self, *args, **kwargs)
1742 # If we don't have any hooks, we want to skip the rest of the logic in
1743 # this function, and just call forward.
1744 if not (self._backward_hooks or self._backward_pre_hooks or self._forward_hooks or self._forward_pre_hooks
1745 or _global_backward_pre_hooks or _global_backward_hooks
1746 or _global_forward_hooks or _global_forward_pre_hooks):
-> 1747 return forward_call(*args, **kwargs)
1749 result = None
1750 called_always_called_hooks = set()
File /opt/conda/lib/python3.11/site-packages/transformers/models/qwen2_vl/modeling_qwen2_vl.py:394, in VisionSdpaAttention.forward(self, hidden_states, cu_seqlens, rotary_pos_emb)
390 def forward(
391 self, hidden_states: torch.Tensor, cu_seqlens: torch.Tensor, rotary_pos_emb: torch.Tensor = None
392 ) -> torch.Tensor:
393 seq_length = hidden_states.shape[0]
--> 394 q, k, v = self.qkv(hidden_states).reshape(seq_length, 3, self.num_heads, -1).permute(1, 0, 2, 3).unbind(0)
395 q = apply_rotary_pos_emb_vision(q.unsqueeze(0), rotary_pos_emb).squeeze(0)
396 k = apply_rotary_pos_emb_vision(k.unsqueeze(0), rotary_pos_emb).squeeze(0)
File /opt/conda/lib/python3.11/site-packages/torch/nn/modules/module.py:1736, in Module._wrapped_call_impl(self, *args, **kwargs)
1734 return self._compiled_call_impl(*args, **kwargs) # type: ignore[misc]
1735 else:
-> 1736 return self._call_impl(*args, **kwargs)
File /opt/conda/lib/python3.11/site-packages/torch/nn/modules/module.py:1747, in Module._call_impl(self, *args, **kwargs)
1742 # If we don't have any hooks, we want to skip the rest of the logic in
1743 # this function, and just call forward.
1744 if not (self._backward_hooks or self._backward_pre_hooks or self._forward_hooks or self._forward_pre_hooks
1745 or _global_backward_pre_hooks or _global_backward_hooks
1746 or _global_forward_hooks or _global_forward_pre_hooks):
-> 1747 return forward_call(*args, **kwargs)
1749 result = None
1750 called_always_called_hooks = set()
File /opt/conda/lib/python3.11/site-packages/torch/nn/modules/linear.py:125, in Linear.forward(self, input)
124 def forward(self, input: Tensor) -> Tensor:
--> 125 return F.linear(input, self.weight, self.bias)
OutOfMemoryError: CUDA out of memory. Tried to allocate 32.00 MiB. GPU 0 has a total capacity of 79.21 GiB of which 33.50 MiB is free. Process 239083 has 79.17 GiB memory in use. Of the allocated memory 78.38 GiB is allocated by PyTorch, and 118.90 MiB is reserved by PyTorch but unallocated. If reserved but unallocated memory is large try setting PYTORCH_CUDA_ALLOC_CONF=expandable_segments:True to avoid fragmentation. See documentation for Memory Management (https://pytorch.org/docs/stable/notes/cuda.html#environment-variables)
難問数学を実際に解けるのか検証
数学の問題を解く性能が高いと言うことなので、プレビュー版を使い、難問数学を実際に解けるか検証してみます!
検証する問題は次の問題です。
- マスターデーモン
- 1996年 IMOインド大会 第5問
- 2009年 IMOドイツ大会 第6問
マスターデーモン
問題はこちらです。

画像を添付して「画像の問題を解いてください」と指示を与えます。
出力された回答はこちら
所以这道题是说,要找出所有大于等于2的整数n,使得 \( \frac{2^n + 1}{n^2} \) 是整数。嗯,看起来有点难度,不过我来试一试。
首先,我需要理解一下这个表达式的意思。就是说,对于某个n,2的n次方加上1,然后再除以n的平方,结果必须是一个整数。也就是说,\( 2^n + 1 \) 是 \( n^2 \) 的倍数。
我先从n=2开始试起。当n=2时,\( 2^2 + 1 = 4 + 1 = 5 \),然后除以 \( 2^2 = 4 \),得到 \( \frac{5}{4} \),这不是整数。所以n=2不符合条件。
接下来是n=3。\( 2^3 + 1 = 8 + 1 = 9 \),然后除以 \( 3^2 = 9 \),得到 \( \frac{9}{9} = 1 \),这是整数。所以n=3是一个解。
再看看n=4。\( 2^4 + 1 = 16 + 1 = 17 \),除以 \( 4^2 = 16 \),得到 \( \frac{17}{16} \),这不是整数。
n=5。\( 2^5 + 1 = 32 + 1 = 33 \),除以 \( 5^2 = 25 \),得到 \( \frac{33}{25} \),也不是整数。
n=6。\( 2^6 + 1 = 64 + 1 = 65 \),除以 \( 6^2 = 36 \),得到 \( \frac{65}{36} \),不是整数。
n=7。\( 2^7 + 1 = 128 + 1 = 129 \),除以 \( 7^2 = 49 \),得到 \( \frac{129}{49} \),大约是2.63,不是整数。
n=8。\( 2^8 + 1 = 256 + 1 = 257 \),除以 \( 8^2 = 64 \),得到 \( \frac{257}{64} \),大约是4.015,不是整数。
看起来,只有n=3满足条件。不过,我得再试几个更大的n,看看有没有其他的解。
n=9。\( 2^9 + 1 = 512 + 1 = 513 \),除以 \( 9^2 = 81 \),得到 \( \frac{513}{81} = 6.333... \),不是整数。
n=10。\( 2^{10} + 1 = 1024 + 1 = 1025 \),除以 \( 10^2 = 100 \),得到 \( \frac{1025}{100} = 10.25 \),不是整数。
n=11。\( 2^{11} + 1 = 2048 + 1 = 2049 \),除以 \( 11^2 = 121 \),得到 \( \frac{2049}{121} \approx 16.93 \),不是整数。
n=12。\( 2^{12} + 1 = 4096 + 1 = 4097 \),除以 \( 12^2 = 144 \),得到 \( \frac{4097}{144} \approx 28.45 \),不是整数。
看起来,n越大,\( 2^n + 1 \) 比 \( n^2 \) 增长得快得多,所以除非 \( n^2 \) 能够整除 \( 2^n + 1 \),否则结果不会是整数。
我再想想,有没有什么数学方法可以确定n=3是唯一的解,或者是否有其他的n也满足条件。
首先,\( 2^n + 1 \) 是一个指数函数,随着n的增加,它增长得非常快。而 \( n^2 \) 是一个二次函数,增长速度相对较慢。所以,当n增大时,\( 2^n + 1 \) 远远大于 \( n^2 \),除非 \( n^2 \) 是 \( 2^n + 1 \) 的约数。
不过,我需要确定是否有其他的n,使得 \( n^2 \) 能够整除 \( 2^n + 1 \)。
我再看看n=1。虽然题目说n>=2,但我还是看看n=1的情况。n=1时,\( 2^1 + 1 = 3 \),除以 \( 1^2 = 1 \),得到3,是整数。所以n=1也是一个解。不过题目要求n>=2,所以n=1不考虑。
再看看n=4到n=12,都没有找到其他的解。可能n=3是唯一的解。
为了更确定,我再试一下n=13。\( 2^{13} + 1 = 8192 + 1 = 8193 \),除以 \( 13^2 = 169 \),得到 \( \frac{8193}{169} = 48.5 \),不是整数。
n=14。\( 2^{14} + 1 = 16384 + 1 = 16385 \),除以 \( 14^2 = 196 \),得到 \( \frac{16385}{196} \approx 83.6 \),不是整数。
n=15。\( 2^{15} + 1 = 32768 + 1 = 32769 \),除以 \( 15^2 = 225 \),得到 \( \frac{32769}{225} = 145.68 \),不是整数。
看来,随着n的增大,结果越来越不可能是整数。可能n=3是唯一的解。
不过,我得想一下,有没有什么数学定理或者方法可以证明n=3是唯一的解。
首先,考虑 \( 2^n + 1 \) 和 \( n^2 \) 的增长速度。指数函数的增长速度远超过二次函数,所以当n增大时,\( 2^n + 1 \) 远远大于 \( n^2 \),除非 \( n^2 \) 能够整除 \( 2^n + 1 \)。
我再考虑一下,如果 \( \frac{2^n + 1}{n^2} \) 是整数,那么 \( n^2 \) 必须是 \( 2^n + 1 \) 的约数。
也就是说,\( 2^n + 1 \) 必须被 \( n^2 \) 整除。
我再看看n=3的情况,\( 2^3 + 1 = 9 \),\( 3^2 = 9 \),确实9能够整除9。
再看看n=5,\( 2^5 + 1 = 33 \),\( 5^2 = 25 \),25不能整除33,因为33除以25是1余8。
n=7,\( 2^7 + 1 = 129 \),\( 7^2 = 49 \),129除以49是2余31,也不是整数。
n=9,\( 2^9 + 1 = 513 \),\( 9^2 = 81 \),513除以81是6余27,不是整数。
n=11,\( 2^{11} + 1 = 2049 \),\( 11^2 = 121 \),2049除以121是16余83,不是整数。
n=13,\( 2^{13} + 1 = 8193 \),\( 13^2 = 169 \),8193除以169是48余57,不是整数。
看来,n=3是唯一的小于等于13的解。
我再试一下n=17。\( 2^{17} + 1 = 131072 + 1 = 131073 \),\( 17^2 = 289 \),131073除以289是多少呢?289×450=129990,131073-129990=1083,289×3=867,1083-867=216,还有余数,所以不是整数。
n=19。\( 2^{19} + 1 = 524288 + 1 = 524289 \),\( 19^2 = 361 \),524289除以361是多少?361×1450=524950,太大了;361×145=52695,524289-52695=471594,不对,我算错了。
看来,手动计算大n的值不太现实,我需要想一个更系统的方法来解决这个问题。
我考虑使用数论的知识。如果 \( n^2 \) 能够整除 \( 2^n + 1 \),那么 \( 2^n + 1 \) 必须是 \( n^2 \) 的倍数。
也就是说,存在一个整数k,使得 \( 2^n + 1 = k \cdot n^2 \)。
我需要找到所有满足这个等式的n>=2。
首先,n=3时,k=1,满足等式。
再看看n=4,\( 2^4 + 1 = 17 \),\( 4^2 = 16 \),17不是16的倍数,所以不存在整数k。
n=5,33不是25的倍数。
n=6,65不是36的倍数。
n=7,129不是49的倍数。
n=8,257不是64的倍数。
n=9,513不是81的倍数。
n=10,1025不是100的倍数。
n=11,2049不是121的倍数。
n=12,4097不是144的倍数。
n=13,8193不是169的倍数。
n=14,16385不是196的倍数。
n=15,32769不是225的倍数。
n=16,65537不是256的倍数。
n=17,131073不是289的倍数。
n=18,262145不是324的倍数。
n=19,524289不是361的倍数。
n=20,1048577不是400的倍数。
看来,n=3是唯一的小于等于20的解。
我再试一下n=21。\( 2^{21} + 1 = 2097152 + 1 = 2097153 \),\( 21^2 = 441 \),2097153除以441是多少?441×4755=2097155,太大了;441×4754=2096997,2097153-2096997=156,有余数,不是整数。
n=22。\( 2^{22} + 1 = 4194304 + 1 = 4194305 \),\( 22^2 = 484 \),4194305除以484是多少?484×8666=4202264,太大了;484×8665=4201820,4194305-4201820=-7515,不对,我算错了。
看来,手动计算大n的值太麻烦了,我需要想一个更聪明的方法。
我考虑使用数学归纳法,看看能否证明对于n>=4,\( 2^n + 1 \) 不是 \( n^2 \) 的倍数。
首先,假设对于某个n>=4,\( 2^n + 1 \) 不是 \( n^2 \) 的倍数,然后看看n+1的情况。
不过,数学归纳法可能不太适合这里,因为我们需要证明的是不存在其他的n满足条件,而不是证明某个性质对所有n成立。
我再想想,有没有什么不等式可以用来限制n的取值范围。
比如,对于n>=4,\( 2^n + 1 \) 和 \( n^2 \) 的增长速度。
我们知道,指数函数的增长速度远超过二次函数,所以当n增大时,\( 2^n + 1 \) 远远大于 \( n^2 \),除非 \( n^2 \) 能够整除 \( 2^n + 1 \)。
我再考虑一下,如果 \( n^2 \) 能够整除 \( 2^n + 1 \),那么 \( 2^n + 1 \) 必须是 \( n^2 \) 的倍数,也就是说,\( 2^n + 1 \) 是 \( n^2 \) 的某个倍数。
我再看看n=3的情况,\( 2^3 + 1 = 9 \),\( 3^2 = 9 \),确实9是9的1倍。
再看看n=4,\( 2^4 + 1 = 17 \),\( 4^2 = 16 \),17不是16的倍数。
n=5,33不是25的倍数。
n=6,65不是36的倍数。
n=7,129不是49的倍数。
n=8,257不是64的倍数。
n=9,513不是81的倍数。
n=10,1025不是100的倍数。
n=11,2049不是121的倍数。
n=12,4097不是144的倍数。
n=13,8193不是169的倍数。
n=14,16385不是196的倍数。
n=15,32769不是225的倍数。
n=16,65537不是256的倍数。
n=17,131073不是289的倍数。
n=18,262145不是324的倍数。
n=19,524289不是361的倍数。
n=20,1048577不是400的倍数。
n=21,2097153不是441的倍数。
n=22,4194305不是484的倍数。
n=23,8388609不是529的倍数。
n=24,16777217不是576的倍数。
n=25,33554433不是625的倍数。
看来,n=3是唯一的小于等于25的解。
我再试一下n=26。\( 2^{26} + 1 = 67108864 + 1 = 67108865 \),\( 26^2 = 676 \),67108865除以676是多少?676×99570=67326720,67108865-67326720=-217855,不对,我算错了。
看来,手动计算大n的值太困难了,我需要考虑其他的数学工具。
我考虑使用数论中的概念,比如费马小定理或者欧拉定理,看看能否找到n和2之间的关系。
首先,费马小定理说,如果p是质数,且p不整除a,那么 \( a^{p-1} \equiv 1 \pmod{p} \)。
不过,这里的情况不太一样,是 \( 2^n + 1 \equiv 0 \pmod{n^2} \),也就是 \( 2^n \equiv -1 \pmod{n^2} \)。
这看起来和费马小定理不太一样,可能需要其他的工具。
我再想想,有没有什么关于指数函数和二次函数的不等式可以用来限制n的取值。
比如,对于n>=4,\( 2^n + 1 \) 远远大于 \( n^2 \),所以除非 \( n^2 \) 能够整除 \( 2^n + 1 \),否则 \( \frac{2^n + 1}{n^2} \) 不是整数。
我再考虑一下,如果 \( n^2 \) 能够整除 \( 2^n + 1 \),那么 \( 2^n + 1 \) 必须是 \( n^2 \) 的倍数,也就是说,\( 2^n + 1 = k \cdot n^2 \),其中k是正整数。
我需要找到所有满足这个等式的n>=2。
首先,n=3时,k=1,满足等式。
再看看n=4,\( 2^4 + 1 = 17 \),\( 4^2 = 16 \),17不是16的倍数,所以不存在整数k。
n=5,33不是25的倍数。
n=6,65不是36的倍数。
n=7,129不是49的倍数。
n=8,257不是64的倍数。
n=9,513不是81的倍数。
n=10,1025不是100的倍数。
n=11,2049不是121的倍数。
n=12,4097不是144的倍数。
n=13,8193不是169的倍数。
n=14,16385不是196的倍数。
n=15,32769不是225的倍数。
n=16,65537不是256的倍数。
n=17,131073不是289的倍数。
n=18,262145不是324的倍数。
n=19,524289不是361的倍数。
n=20,1048577不是400的倍数。
n=21,2097153不是441的倍数。
n=22,4194305不是484的倍数。
n=23,8388609不是529的倍数。
n=24,16777217不是576的倍数。
n=25,33554433不是625的倍数。
看来,n=3是唯一的小于等于25的解。
我再试一下n=27。\( 2^{27} + 1 = 134217728 + 1 = 134217729 \),\( 27^2 = 729 \),134217729除以729是多少?729×18408=134217732,134217729-134217732=-3,有余数,不是整数。
n=28。\( 2^{28} + 1 = 268435456 + 1 = 268435457 \),\( 28^2 = 784 \),268435457除以784是多少?784×34250=268436000,268435457-268436000=-543,有余数,不是整数。
n=29。\( 2^{29} + 1 = 536870912 + 1 = 536870913 \),\( 29^2 = 841 \),536870913除以841是多少?841×64000=536960000,536870913-536960000=-89087,有余数,不是整数。
n=30。\( 2^{30} + 1 = 1073741824 + 1 = 1073741825 \),\( 30^2 = 900 \),1073741825除以900是多少?900×1193046=1073741400,1073741825-1073741400=425,有余数,不是整数。
看来,n=3是唯一的小于等于30的解。
我再试一下n=31。\( 2^{31} + 1 = 2147483648 + 1 = 2147483649 \),\( 31^2 = 961 \),2147483649除以961是多少?961×2234640=2147482640,2147483649-2147482640=1009,有余数,不是整数。
n=32。\( 2^{32} + 1 = 4294967296 + 1 = 4294967297 \),\( 32^2 = 1024 \),4294967297除以1024是多少?1024×4195200=4294967296,4294967297-4294967296=1,有余数,不是整数。
n=33。\( 2^{33} + 1 = 8589934592 + 1 = 8589934593 \),\( 33^2 = 1089 \),8589934593除以1089是多少?1089×788500=8589934500,8589934593-8589934500=93,有余数,不是整数。
n=34。\( 2^{34} + 1 = 17179869184 + 1 = 17179869185 \),\( 34^2 = 1156 \),17179869185除以1156是多少?1156×1486300=17179869160,17179869185-17179869160=25,有余数,不是整数。
n=35。\( 2^{35} + 1 = 34359738368 + 1 = 34359738369 \),\( 35^2 = 1225 \),34359738369除以1225是多少?1225×2805000=34359750000,34359738369-34359750000=-11631,有余数,不是整数。
n=36。\( 2^{36} + 1 = 68719476736 + 1 = 68719476737 \),\( 36^2 = 1296 \),68719476737除以1296是多少?1296×5299200=68719477760,68719476737-68719477760=-1023,有余数,不是整数。
看来,n=3是唯一的小于等于36的解。
我再试一下n=37。\( 2^{37} + 1 = 137438953472 + 1 = 137438953473 \),\( 37^2 = 1369 \),137438953473除以1369是多少?1369×10039200=137438953480,137438953473-137438953480=-7,有余数,不是整数。
n=38。\( 2^{38} + 1 = 274877906944 + 1 = 274877906945 \),\( 38^2 = 1444 \),274877906945除以1444是多少?1444×18999900=274877907060,274877906945-274877907060=-115,有余数,不是整数。
n=39。\( 2^{39} + 1 = 549755813888 + 1 = 549755813889 \),\( 39^2 = 1521 \),549755813889除以1521是多少?1521×3614400=549755813600,549755813889-549755813600=289,有余数,不是整数。
n=40。\( 2^{40} + 1 = 1099511627776 + 1 = 1099511627777 \),\( 40^2 = 1600 \),1099511627777除以1600是多少?1600×68719400=1099511628000,1099511627777-1099511628000=-223,有余数,不是整数。
看来,n=3是唯一的小于等于40的解。
我再试一下n=41。\( 2^{41} + 1 = 2199023255552 + 1 = 2199023255553 \),\( 41^2 = 1681 \),2199023255553除以1681是多少?1681×13081000=2199023256000,2199023255553-2199023256000=-447,有余数,不是整数。
n=42。\( 2^{42} + 1 = 4398046511104 + 1 = 4398046511105 \),\( 42^2 = 1764 \),4398046511105除以1764是多少?1764×24927000=4398046512000,4398046511105-4398046512000=-895,有余数,不是整数。
n=43。\( 2^{43} + 1 = 8796093022208 + 1 = 8796093022209 \),\( 43^2 = 1849 \),8796093022209除以1849是多少?1849×47570000=8796093020000,8796093022209-8796093020000=2209,有余数,不是整数。
n=44。\( 2^{44} + 1 = 17592186044416 + 1 = 17592186044417 \),\( 44^2 = 1936 \),17592186044417除以1936是多少?1936×90337000=17592186044800,17592186044417-17592186044800=-383,有余数,不是整数。
n=45。\( 2^{45} + 1 = 35184372088832 + 1 = 35184372088833 \),\( 45^2 = 2025 \),35184372088833除以2025是多少?2025×173770000=35184372000000,35184372088833-35184372000000=88833,有余数,不是整数。
n=46。\( 2^{46} + 1 = 70368744177664 + 1 = 70368744177665 \),\( 46^2 = 2116 \),70368744177665除以2116是多少?2116×332400000=70368744240000,70368744177665-70368744240000=-62335,有余数,不是整数。
n=47。\( 2^{47} + 1 = 140737488355328 + 1 = 140737488355329 \),\( 47^2 = 2209 \),140737488355329除以2209是多少?2209×637000000=140737488200000,140737488355329-140737488200000=155329,有余数,不是整数。
n=48。\( 2^{48} + 1 = 281474976710656 + 1 = 281474976710657 \),\( 48^2 = 2304 \),281474976710657除以2304是多少?2304×1221900000=281474976710400,281474976710657-281474976710400=257,有余数,不是整数。
看来,n=3是唯一的小于等于48的解。
我再试一下n=49。\( 2^{49} + 1 = 562949953421312 + 1 = 562949953421313 \),\( 49^2 = 2401 \),562949953421313除以2401是多少?2401×2344600000=562949953421600,562949953421313-562949953421600=-287,有余数,不是整数。
n=50。\( 2^{50} + 1 = 1125899906842624 + 1 = 1125899906842625 \),\( 50^2 = 2500 \),1125899906842625除以2500是多少?2500×4503599627370=1125899906842500,1125899906842625-1125899906842500=125,有余数,不是整数。
n=51。\( 2^{51} + 1 = 2251799813685248 + 1 = 2251799813685249 \),\( 51^2 = 2601 \),2251799813685249除以2601是多少?2601×8659000000=2251799813686000,2251799813685249-2251799813686000=-751,有余数,不是整数。
n=52。\( 2^{52} + 1 = 4503599627370496 + 1 = 4503599627370497 \),\( 52^2 = 2704 \),4503599627370497除以2704是多少?2704×166520000000=4503599627370400,4503599627370497-4503599627370400=97,有余数,不是整数。
n=53。\( 2^{53} + 1 = 9007199254740992 + 1 = 9007199254741000 - 9007199254740993 \),\( 53^2 = 2809 \),9007199254740993除以2809是多少?2809×320600000000=8997199254740800,9007199254740993-8997199254740800=10000000000000000 - 93,有余数,不是整数。
n=54。\( 2^{54} + 1 = 18014398509481984 + 1 = 18014398509481985 \),\( 54^2 = 2916 \),18014398509481985除以2916是多少?2916×617500000000=18014398509480000,18014398509481985-18014398509480000=1985,有余数,不是整数。
n=55。\( 2^{55} + 1 = 36028797018963968 + 1 = 36028797018963969 \),\( 55^2 = 3025 \),36028797018963969除以3025是多少?3025×1200000000000=36028797018960000,36028797018963969-36028797018960000=3969,有余数,不是整数。
n=56。\( 2^{56} + 1 = 72057594037927936 + 1 = 72057594037927937 \),\( 56^2 = 3136 \),72057594037927937除以3136是多少?3136×2300000000000=72057594037920000,72057594037927937-72057594037920000=7937,有余数,不是整数。
n=57。\( 2^{57} + 1 = 14解き進めてくれている感じはありますが、整数が1ずつ増えていき、ゴールが見えず途中で終了としてしまいました。
うまく回答できなかったのですが、動画を撮ったので載せておきます。
1996年 IMOインド大会 第5問
次の問題はこちらです。

こちらも画像を与えて問題を解くように指示をします。
出力された回答はこちら
所以这个题目是关于一个凸六边形ABCDEF的,它有三条边是平行的:AB平行于DE,BC平行于EF,CD平行于FA。然后,题目还提到了三个三角形:FAB、BCD、DEF,它们的外接圆半径分别是RA、RC、RE。最后,六边形的周长是P,要我们证明RA + RC + RE >= P/2。
首先,我需要理解一下这个六边形的结构。有三条边两两平行,这可能意味着某些对边是平行的,或者有其他的几何关系。可能需要利用平行线的性质来找到一些角度或者边长的关系。
我先画一个六边形来帮助理解。假设我有六个顶点A、B、C、D、E、F,按照顺序连接起来形成六边形。给定AB // DE,BC // EF,CD // FA。
首先,因为AB // DE,所以直线AB和DE之间的距离应该是恒定的,或者它们的斜率相同,如果在坐标系中的话。类似地,BC // EF,CD // FA。
可能需要考虑使用向量或者坐标几何来解决这个问题,因为涉及到平行关系和距离。
不过,题目中提到了外接圆半径,所以可能需要使用三角形的外接圆公式,比如RA = (ABC)/(2面积),其中ABC是三角形FAB的三条边。
但是,我可能需要找到一种方法来关联这三个外接圆半径和六边形的周长P。
可能需要找到六边形的周长P和这三个三角形的外接圆半径之间的关系。
首先,六边形的周长P是所有边长的和:AB + BC + CD + DE + EF + FA。
而我们需要证明RA + RC + RE >= P/2。
可能需要找到RA、RC、RE和边长之间的关系。
首先,回忆一下三角形的外接圆半径公式:RA = ABC / (2 * 面积),其中ABC是三角形的三条边,面积是三角形的面积。
但是,我可能需要找到一种更直接的关联。
也许可以考虑使用三角形的正弦定理,因为正弦定理涉及到边和角以及外接圆半径。
正弦定理说,在任何一个三角形中,边长与角的正弦值和外接圆半径有关:a / sin A = 2R,其中a是边长,A是对应的角,R是外接圆半径。
所以,对于三角形FAB,有AB / sin F = 2RA。
类似地,对于三角形BCD,有BC / sin D = 2RC。
对于三角形DEF,有DE / sin F = 2RE。
不过,这里可能需要更多的信息来建立联系。
可能需要找到这些三角形之间的关系,或者找到六边形内部的角度或者其他的几何关系。
也许可以考虑将六边形分成三个三角形,然后利用某些不等式来证明RA + RC + RE >= P/2。
不过,六边形分成三个三角形可能有多种方法,需要确定一种合适的方法。
或者,可以考虑使用凸六边形的性质,比如它的内角和是720度,或者其他的性质。
可能需要找到六边形的面积和外接圆半径之间的关系,但是题目中没有提到面积,所以可能不太直接。
或者,可以考虑使用三角形的周长和外接圆半径之间的关系。
比如,三角形的周长是AB + BC + CA,面积是S,外接圆半径是R,有R = ABC / (4S)。
不过,这可能不太直接帮助我证明RA + RC + RE >= P/2。
可能需要找到一种方法来比较三个外接圆半径的和与六边形的周长的一半。
也许可以考虑使用不等式,比如均值不等式,来估计RA + RC + RE的最小值。
比如,RA + RC + RE >= 3 * (RA * RC * RE)^(1/3),但是这可能不太适用,因为我们需要和P/2比较。
可能需要找到RA、RC、RE和P之间的具体关系。
或者,可以考虑将六边形的周长表示成与三角形的边长相关的形式。
比如,六边形的周长P = AB + BC + CD + DE + EF + FA。
而三角形FAB的周长是FA + AB + BF,不过可能需要找到这些量之间的关系。
可能需要更多的几何知识来解决这个问题。
或者,可以考虑使用向量或者坐标几何来表示这个六边形,然后计算相关的量。
比如,假设六边形在坐标系中,给定六个顶点的坐标,然后计算边长和外接圆半径。
不过,这可能比较复杂,而且可能不是最有效的方法。
可能需要寻找更优雅的几何证明方法。
也许可以考虑使用三角形的某些性质,比如外接圆半径和边长之间的关系,以及平行线带来的等角性或者相似性。
比如,因为AB // DE,所以三角形FAB和三角形FDE可能有某些关系,比如相似或者有相等的角。
不过,我需要更仔细地分析这一点。
假设AB // DE,那么角FAB和角FDE可能有某种关系,比如它们的对应角相等。
不过,这可能需要具体分析。
可能需要更深入地研究六边形的结构。
或者,可以考虑将六边形分成三个梯形或者平行四边形,因为有对边平行。
不过,六边形只有三条边是平行的,可能不是所有的对边都平行。
可能需要具体分析这些平行关系带来的几何约束。
也许可以考虑使用向量的方法来表示这些平行关系,然后找到边长和外接圆半径之间的关系。
比如,设向量AB和向量DE平行,那么存在一个实数k使得DE = k * AB。
类似地,BC // EF,CD // FA。
可能需要找到这些向量之间的关系,然后表示出六边形的周长和外接圆半径。
不过,这可能比较复杂,我可能需要寻找更简单的方法。
或者,可以考虑使用三角形的某些不等式,比如RA >= (AB + BC + CA)/6,不过我不确定这个不等式是否成立。
如果RA >= (AB + BC + CA)/6,那么RA + RC + RE >= (AB + BC + CA)/6 + (BC + CD + DA)/6 + (DE + EF + FA)/6 = (AB + 2BC + 2CD + DE + 2EF + FA)/6。
但是,六边形的周长是AB + BC + CD + DE + EF + FA,所以RA + RC + RE >= (P + BC + CD + EF)/6,这并不直接导致RA + RC + RE >= P/2。
所以,这个思路可能不太行。
可能需要寻找其他的不等式或者方法。
或者,可以考虑使用三角形的某些恒等式,比如涉及外接圆半径和内切圆半径的公式,但是题目中没有提到内切圆,可能不太适用。
可能需要回到平行线的性质,看看能否找到一些角度或者边长的关系,从而建立RA、RC、RE和P之间的联系。
比如,因为AB // DE,所以角FAB和角FDE可能有某种关系。
不过,我需要具体分析一下。
假设我有六边形ABCDEF,其中AB // DE,BC // EF,CD // FA。
可能可以考虑连接某些对角线,看看能否形成一些特殊的图形或者关系。
比如,连接AC、BD、CE等,看看能否找到一些相似三角形或者其他的几何关系。
不过,这可能比较复杂,我可能需要更系统的方法。
或者,可以考虑使用三角形的某些恒等式,比如涉及外接圆半径和边长的公式,然后尝试将它们加起来,看看能否得到RA + RC + RE >= P/2。
比如,对于三角形FAB,有RA = AB / (2 sin F),其中F是角F的度数。
类似地,RC = BC / (2 sin D),RE = DE / (2 sin F)。
不过,这里可能需要更多的信息来建立联系。
可能需要找到角F、D等的具体值,或者找到它们之间的关系。
这可能需要更深入的几何分析,我可能需要查阅一些相关的几何知识。
或者,可以考虑使用三角形的某些不等式,比如RA >= AB/2,不过我不确定这个不等式是否成立。
如果RA >= AB/2,那么RA + RC + RE >= AB/2 + BC/2 + CD/2 + DE/2 + EF/2 + FA/2 = P/2,这就证明了所需的不等式。
所以,如果我能证明RA >= AB/2,那么问题就解决了。
不过,我需要验证这个不等式是否成立。
考虑三角形FAB,它的外接圆半径RA = AB / (2 sin F),其中F是角F的度数。
因为sin F <=1,所以RA >= AB /2,当且仅当sin F=1时等号成立,也就是角F=90度时。
所以,对于任意三角形,RA >= AB/2,类似地,RC >= BC/2,RE >= DE/2。
因此,RA + RC + RE >= AB/2 + BC/2 + CD/2 + DE/2 + EF/2 + FA/2 = P/2。
所以,这个不等式成立了,从而证明了所需的不等式。
不过,我需要确认一下这个推理是否正确。
首先,RA = AB / (2 sin F),其中F是角F的度数。
因为sin F <=1,所以RA >= AB/2,等号当且仅当sin F=1,即角F=90度时成立。
类似地,RC >= BC/2,RE >= DE/2。
所以,RA + RC + RE >= AB/2 + BC/2 + CD/2 + DE/2 + EF/2 + FA/2 = P/2。
这个不等式是成立的,所以我们可以得出RA + RC + RE >= P/2。
不过,我需要确认一下这个证明是否考虑了六边形的特定条件,比如三条边平行。
在这个证明中,我只使用了三角形的外接圆半径公式和sin F <=1的事实,没有直接使用六边形的平行边条件。
这可能意味着这个不等式对于任意的三角形都成立,而不仅仅适用于这个特定的六边形。
不过,题目中明确提到了六边形的三条边平行,所以可能需要确保这个证明在六边形的条件下仍然成立。
也许,六边形的平行边条件可以保证角F、D等的取值范围,从而确保sin F <=1,等等。
不过,无论如何,在三角形中,sin F的取值范围总是从0到1,所以RA >= AB/2总是成立的。
所以,我认为这个证明是正确的。
因此,我们可以得出结论:RA + RC + RE >= P/2。
这完成了所需的证明。
**总结**
通过使用三角形的外接圆半径公式RA = AB / (2 sin F),并注意到sin F <=1,我们证明了RA >= AB/2,类似地,RC >= BC/2,RE >= DE/2。
因此,RA + RC + RE >= AB/2 + BC/2 + CD/2 + DE/2 + EF/2 + FA/2 = P/2,其中P是六边形的周长。
从而,我们证明了所需的不等式RA + RC + RE >= P/2。
这个证明不依赖于六边形的特定平行边条件,因为不等式对于任意三角形都成立。
**最终答案**
\boxed{R_{A} + R_{C} + R_{E} \geq \dfrac{P}{2}}まとめと最終回答の日本語訳はこちら
**まとめ**
三角形の外接円の半径の公式を使用すると、RA = AB / (2 sin F) となり、sin F <=1 であることから、RA >= AB/2 であることが示され、同様に、RC >= BC/2、RE >= DE/2 であることが示されました。
したがって、RA + RC + RE >= AB/2 + BC/2 + CD/2 + DE/2 + EF/2 + FA/2 = P/2 となります。ここで、P は六角形の周囲です。
したがって、必要な不等式 RA + RC + RE >= P/2 を証明したことになります。
この証明は、三角形であればどのような三角形に対しても成り立つため、六角形の特定の平行四辺形の条件に依存するものではありません。
**最終回答**
R_{A} + R_{C} + R_{E} ≥ P/2回答を数学オリンピック20世紀最難問で確認しましたが、合ってそうです!
2009年 IMOドイツ大会 第6問
次がこちらの問題です。

一問目と同じように、画像を与えて「画像の問題を解いてください」と指示を与えます。
出力された回答はこちら
Let's tackle this problem step by step. So, we have a sequence of distinct positive integers \(a_1, a_2, \ldots, a_n\), and a set \(M\) consisting of \(n-1\) positive integers, none of which is equal to the sum \(s = a_1 + a_2 + \ldots + a_n\). We have a frog starting at 0 on the number line, and it makes \(n\) jumps towards the positive direction, where each jump's length is one of the integers \(a_1, a_2, \ldots, a_n\), in some order. The task is to prove that we can choose the order of these jumps such that the frog never lands on any point in \(M\) during its jumps.
First, let's understand the problem better. We have a frog that starts at 0 and makes \(n\) jumps, each of length equal to one of the \(a_i\)'s, in some order. We need to permute the sequence \(a_1, a_2, \ldots, a_n\) so that the cumulative sum at any point (after each jump) is not equal to any element in \(M\).
Given that \(M\) has \(n-1\) elements and none of them is equal to \(s\), the sum of all \(a_i\)'s, we need to ensure that none of the partial sums match any element in \(M\).
Let's consider the sequence of positions the frog occupies after each jump. Let's denote the permutation of jumps as \(b_1, b_2, \ldots, b_n\), where each \(b_i\) is one of the \(a_j\)'s. Then, the positions after each jump are:
\[
p_1 = b_1, \quad p_2 = p_1 + b_2, \quad p_3 = p_2 + b_3, \quad \ldots, \quad p_n = p_{n-1} + b_n
\]
Our goal is to choose the permutation \((b_1, b_2, \ldots, b_n)\) such that none of the \(p_k\) (\(k = 1, 2, \ldots, n-1\)) are in \(M\).
Since \(M\) has \(n-1\) elements and there are \(n-1\) possible landing points (\(p_1, p_2, \ldots, p_{n-1}\)), if we can find a permutation where these points do not coincide with \(M\), we're done.
Let's think about the possible sums that the frog can land on. Each \(p_k\) is the sum of the first \(k\) jumps in the permutation. So, \(p_k = b_1 + b_2 + \ldots + b_k\), for \(k = 1\) to \(n-1\).
Given that all \(a_i\) are distinct and positive integers, and \(M\) is a set of \(n-1\) distinct positive integers not equal to \(s\), we need to arrange the jumps so that no partial sum matches any element in \(M\).
One approach could be to consider all possible permutations of the jumps and see if at least one avoids landing on \(M\). However, with \(n\) jumps, there are \(n!\) permutations, which is a large number, and checking each one isn't practical. We need a smarter way.
Let's consider the properties of the sums. Since all \(a_i\) are distinct and positive, the order in which jumps are taken affects the path the frog takes, potentially allowing us to avoid landing on \(M\).
Another angle: perhaps we can construct a permutation where the partial sums avoid \(M\). For example, if we order the jumps in a way that the partial sums are either all less than the smallest element in \(M\) or all greater than the largest element in \(M\), then we're safe.
However, since \(M\) contains \(n-1\) elements, and the frog makes \(n-1\) jumps, it's possible that with careful selection, we can avoid landing on any of them.
Wait a minute, let's think about the problem in terms of graph theory or some other framework, but that might be overcomplicating it.
Let's try a smaller example to get some intuition.
Suppose \(n = 3\), so we have three distinct positive integers \(a_1, a_2, a_3\), and \(M\) has \(n-1 = 2\) elements, neither of which is equal to \(s = a_1 + a_2 + a_3\).
We need to permute the jumps \(a_1, a_2, a_3\) such that the intermediate sums \(p_1\) and \(p_2\) do not equal any element in \(M\).
Let's say \(M = \{m_1, m_2\}\), with \(m_1 < m_2\), and \(s > m_2\).
We need to choose the order of jumps so that neither \(b_1\) nor \(b_1 + b_2\) equals \(m_1\) or \(m_2\).
Given that there are only two elements in \(M\) and three possible jumps, it's plausible that we can find a permutation where the partial sums avoid \(M\).
For example, if \(a_1 = 1\), \(a_2 = 2\), \(a_3 = 4\), and \(M = \{3, 5\}\), then \(s = 7\), which is not in \(M\).
Possible permutations:
1. \(1, 2, 4\): positions \(1, 3, 7\) → lands on 3, which is in \(M\).
2. \(1, 4, 2\): positions \(1, 5, 7\) → lands on 5, which is in \(M\).
3. \(2, 1, 4\): positions \(2, 3, 7\) → lands on 3.
4. \(2, 4, 1\): positions \(2, 6, 7\) → does not land on 3 or 5.
5. \(4, 1, 2\): positions \(4, 5, 7\) → lands on 5.
6. \(4, 2, 1\): positions \(4, 6, 7\) → does not land on 3 or 5.
So, in this case, permutations 4 and 6 avoid landing on \(M\).
This suggests that for \(n = 3\), it's possible to find a permutation that avoids \(M\).
Now, let's try \(n = 4\), \(a_1 = 1\), \(a_2 = 2\), \(a_3 = 4\), \(a_4 = 8\), \(M = \{3, 5, 6\}\), \(s = 15\).
We need to permute \(1, 2, 4, 8\) such that \(p_1, p_2, p_3\) do not equal 3, 5, or 6.
Let's consider permutation \(1, 2, 4, 8\): positions \(1, 3, 7, 15\) → lands on 3.
Permutation \(1, 4, 2, 8\): positions \(1, 5, 7, 15\) → lands on 5 and 7.
Permutation \(2, 1, 4, 8\): positions \(2, 3, 7, 15\) → lands on 3.
Permutation \(2, 4, 1, 8\): positions \(2, 6, 7, 15\) → lands on 6 and 7.
Permutation \(4, 1, 2, 8\): positions \(4, 5, 7, 15\) → lands on 5 and 7.
Permutation \(4, 2, 1, 8\): positions \(4, 6, 7, 15\) → lands on 6 and 7.
Permutation \(8, 1, 2, 4\): positions \(8, 9, 11, 15\) → does not land on 3, 5, or 6.
Permutation \(8, 2, 1, 4\): positions \(8, 10, 11, 15\) → does not land on 3, 5, or 6.
Permutation \(8, 4, 1, 2\): positions \(8, 12, 13, 15\) → does not land on 3, 5, or 6.
Permutation \(8, 4, 2, 1\): positions \(8, 12, 14, 15\) → does not land on 3, 5, or 6.
So, in this case, multiple permutations avoid landing on \(M\).
This suggests that for \(n = 4\), it's also possible to find a permutation that avoids \(M\).
Is there a general pattern or theorem that can help us prove this for any \(n\)?
Let's consider the problem in terms of graph theory. We can think of the partial sums as paths in a graph where each node represents a position on the number line, and edges represent jumps of length equal to one of the \(a_i\)'s.
However, this might not be the most straightforward approach.
Another idea: since all \(a_i\) are distinct and positive, and \(M\) has \(n-1\) elements, none of which is equal to \(s\), perhaps we can use the pigeonhole principle.
But the pigeonhole principle typically tells us that if we have more pigeons than holes, at least one hole has more than one pigeon. In this case, we have \(n-1\) landing points and \(n-1\) elements in \(M\), so it's possible that some landing points coincide with \(M\), but not necessarily all.
Wait, but we need to ensure that none of the landing points coincide with \(M\).
Perhaps we can consider the differences between the partial sums and the elements in \(M\), but I'm not sure.
Let's think differently. Suppose we fix an order of jumps, say \(a_1, a_2, \ldots, a_n\), leading to partial sums \(p_k = a_1 + a_2 + \ldots + a_k\) for \(k = 1\) to \(n-1\).
We need none of these \(p_k\) to be in \(M\).
Given that \(M\) has \(n-1\) elements, and there are \(n-1\) partial sums, if we can find a permutation where these partial sums are distinct and none equals any element in \(M\), we're done.
But are the partial sums necessarily distinct for some permutation?
Not necessarily, since different permutations can lead to the same partial sums.
Wait, but since all \(a_i\) are distinct, the partial sums in a given permutation are distinct because each \(a_i\) is unique.
So, in any permutation, the sequence of partial sums \(p_1, p_2, \ldots, p_{n-1}\) are distinct.
Given that, and since \(M\) has \(n-1\) elements, none of which is equal to \(s\), perhaps we can choose a permutation where the partial sums avoid \(M\).
But how can we guarantee that?
Let's consider the set of all possible partial sums across all permutations.
Each permutation gives a unique sequence of partial sums, but these sequences overlap in terms of the actual sums.
Wait, no. Each permutation gives a unique sequence of partial sums, but the sums themselves can repeat across different permutations.
For example, in the \(n=3\) case with \(a_1=1\), \(a_2=2\), \(a_3=4\), the partial sums for permutation \(1,2,4\) are \(1,3\), and for \(2,1,4\) are \(2,3\), so both have 3 as a partial sum.
Similarly, for \(1,4,2\): \(1,5\); for \(4,1,2\): \(4,5\); for \(2,4,1\): \(2,6\); for \(4,2,1\): \(4,6\).
So, some partial sums can appear in multiple permutations.
Given that, perhaps we can find a permutation where the partial sums don't coincide with \(M\).
But this seems too vague.
Let's consider the problem in terms of avoiding specific values.
We need to choose a permutation such that for each \(k\) from 1 to \(n-1\), \(p_k \neq m\) for any \(m \in M\).
Given that \(M\) has \(n-1\) elements, and there are \(n!\) possible permutations, it's likely that at least one permutation exists where none of the partial sums match any element in \(M\).
But how to prove it?
Perhaps we can use induction on \(n\).
Base case: \(n=2\). Then \(M\) has \(n-1=1\) element, say \(m\), and \(s = a_1 + a_2\), with \(s \neq m\).
We need to choose the order of jumps \(a_1, a_2\) such that neither \(a_1\) nor \(a_1 + a_2\) equals \(m\).
Since \(s \neq m\), only \(p_1 = a_1\) needs to avoid \(m\).
If \(a_1 \neq m\), choose the permutation starting with \(a_1\); otherwise, start with \(a_2\).
Since \(a_1\) and \(a_2\) are distinct and positive, and \(m\) is a single element not equal to \(s\), at least one of them is not equal to \(m\).
Thus, the base case holds.
Inductive step: Assume the statement is true for some \(n \geq 2\), and prove it for \(n+1\).
Given \(n+1\) distinct positive integers \(a_1, a_2, \ldots, a_{n+1}\), and a set \(M\) of \(n\) distinct positive integers, none equal to \(s = a_1 + a_2 + \ldots + a_{n+1}\).
We need to find a permutation of jumps such that none of the partial sums \(p_1, p_2, \ldots, p_n\) equals any element in \(M\).
Let's fix one of the \(a_i\), say \(a_{n+1}\), and consider the remaining \(n\) jumps \(a_1, a_2, \ldots, a_n\).
By the inductive hypothesis, there exists a permutation of these \(n\) jumps such that none of the partial sums \(p_1, p_2, \ldots, p_{n-1}\) equals any element in \(M'\), where \(M'\) is the set \(M\) minus \(s - a_{n+1}\), assuming \(s - a_{n+1}\) is not in \(M\).
Wait, this seems complicated.
Alternatively, perhaps we can consider the problem in terms of graph theory, where each permutation corresponds to a path in a graph, and we need to find a path that avoids certain nodes.
But that might not lead us anywhere.
Let's try another approach.
Consider the set of all possible partial sums across all permutations.
Each partial sum is of the form \(p_k = b_1 + b_2 + \ldots + b_k\), where \(b_i\) is a permutation of \(a_i\).
Since all \(a_i\) are distinct, each partial sum is unique within a permutation, but across permutations, some sums can repeat.
Our goal is to choose a permutation where none of the partial sums coincide with \(M\).
Given that \(M\) has \(n-1\) elements and there are \(n-1\) partial sums, if we can ensure that the partial sums are distinct and none equals any element in \(M\), we're done.
But how to guarantee that?
Perhaps we can use the fact that the \(a_i\) are distinct and positive, and \(M\) has \(n-1\) elements, none equal to \(s\).
Let's consider the set \(S\) of all possible partial sums across all permutations.
Each partial sum is a sum of some subset of \(a_i\), but since we're considering permutations, each partial sum corresponds to a unique sequence.
Wait, no. Eachこちらも全然回答が終了しませんでした。おそらくこれが公式ページに限界として書かれていた再帰的推論の部分でしょう。
なお、数学やプログラミングの分野で好成績なベンチマークを残したQwQについて詳しく知りたい方は、下記の記事を合わせてご確認ください。

まとめ
本記事ではQVQ-72B-Previewの概要から使い方までお伝えしました。これまではテキストベースで数学の問題を解き、好成績を残すモデルが多かったですが、視覚推論に力を入れたQVQ-72B-Previewによって、これまで以上に正確に数学の問題を解くことが可能になるでしょう。
ぜひ本記事を参考に使ってみてください!
最後に
いかがだったでしょうか
生成AIを活用した効率化や革新的なビジネス展開をお考えの方へ。貴社の課題に応じた最適な活用方法をご提案します。
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、大規模言語モデル(LLM)を対象に、言語理解能力、生成能力、応答速度の各側面について比較・検証した資料も配布しております。この機会にぜひご活用ください。





