【QwQ-32B-preview】Qwenベースの推論モデル登場!数学タスクでo1と徹底比較

2025年3月6日、 Alibaba CloudのAI研究チーム「Qwen」から新たなLLMが登場しました!
強化学習(RL)を大規模に活用した訓練手法により、推論・問題解決能力を飛躍的に高めており、6710億パラメータの巨大モデル「DeepSeek-R1」に匹敵する性能を達成したと発表されています。
- 数学やプログラミングの分野で好成績なベンチマーク
- Qwen2.5をベースにしたLLM
- 人と同じような推論プロセスを持つ
本記事では、「QwQ-32B」について解説をして、google colaboratoryでの実装方法を紹介します。本記事を最後まで読めば、使い道や実装方法を理解できます。
ぜひ最後までご覧ください!
QwQ-32Bの概要
「QwQ-32B」は、未知の境界に深く向き合うことを目指したLLMであり、AI推論機能の向上を目的に設計されており、RoPE位置エンコーディング・SwiGLU活性化関数・RMSNorm正規化などの技術を採用し、最大131,072トークンもの長大なコンテキスト入力に対応できるのも特徴です。
さらにエージェント機能(ツール使用や環境からのフィードバックに応じた思考の調整)も統合されており、状況に応じて批判的思考を行う能力も備えています。
「QwQ-32B」は、特に数学やプログラミングの分野で顕著な成果を上げていますが、限界もあります。
- 言語の混合とコードスイッチング:言語を混合したり、予期せず言語を切り替えたりする可能性があり、応答の明瞭さに影響する可能性がある。
- 再帰的な推論ループ:循環的な推論パターンに入る可能性があり、結論に至らない冗長な応答を生成する場合がある。
- 安全性と倫理的考慮事項:信頼性が高く安全なパフォーマンスを確保するために、安全対策を必要とし、QwQを使用する際には注意を払う必要がある。
- パフォーマンスとベンチマークの制限:数学とコーディングに優れているが、常識的な推論や微妙な言語理解などの他の分野では改善の余地がある。
QwQ-32Bの性能
QwQ-32Bは、深い思考と内省のプロセスを通じて、数学やプログラミングにおける理解を飛躍的に向上しています。このモデル自身が課題を分析し、仮説検証をすることでより最適な解決策を見つけることが可能です。
その結果、以下のようなベンチマークで優れたパフォーマンスを達成しています。
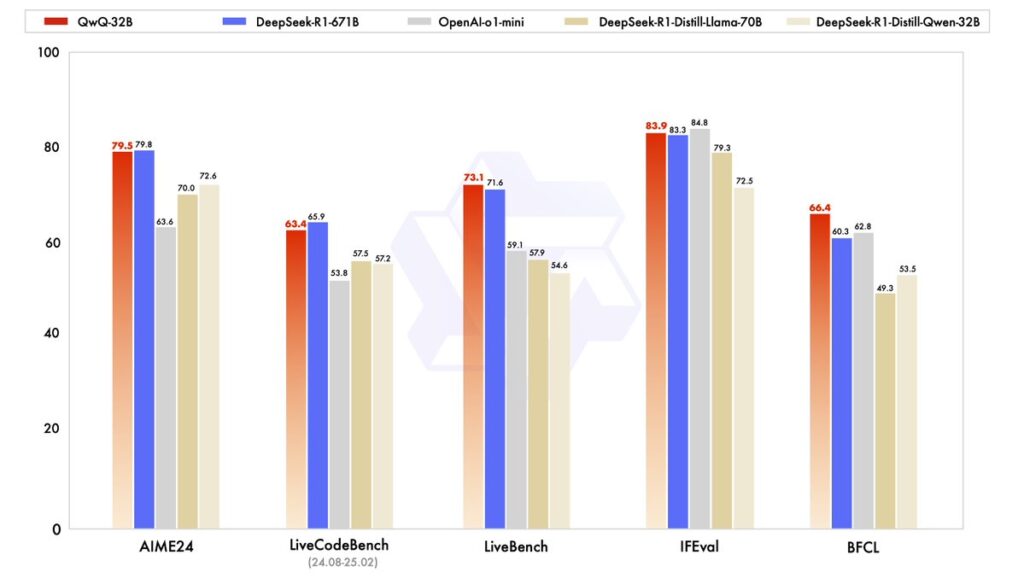
また、QwQ-32Bのプレビュー版でも、以下のようなベンチマーク性能を示しています。
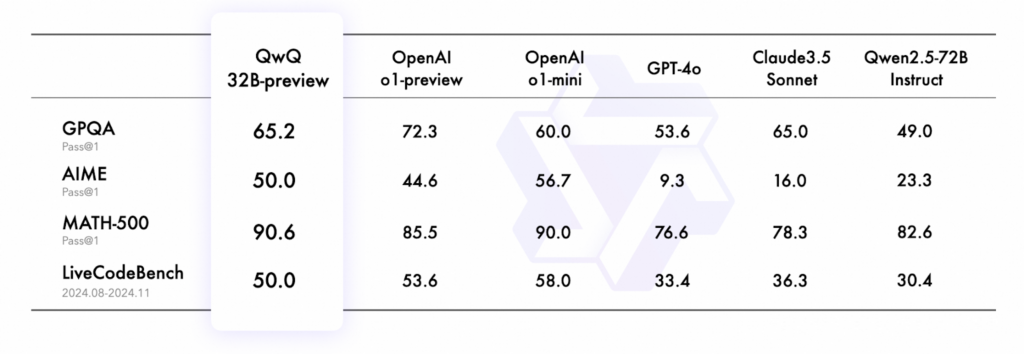
- GPQA:科学的な問題解決能力を評価するためのベンチマーク。このベンチマークは、単にインターネットで検索するだけでは答えを見つけられないような問題を含み、LLMの本質的な推論能力を試す設計。小学生から大学卒業レベルの科学的知識を扱う問題を含んでおり、博士号保持者や博士課程の学生でも65%程度のスコアに留まる。
- AIME:アメリカの数学コンテストの一環として実施される試験で、特に数学的思考力と問題解決能力を評価。算数、代数、幾何学、数列・数論、確率論が含まれる。
- MATH-500:数学に特化したベンチマークで、500個の多様な問題を含む包括的なテストケース。中等教育から大学レベルまで幅広い数学分野をカバー。
- LiveCodeBench:プログラミング能力を評価するための実践的なベンチマーク。特にリアルワールドのプログラミング問題に焦点を当てている。コード生成能力、バグの修正、アルゴリズム設計、プログラムの最適化を測定できる。
推論プロセス
公式ページに記載されている算数問題をもとにQwQの推論プロセスついて解説します。
算数問題の解答に至るQwQの推論プロセスは、試行錯誤と深い考察が特徴です。
QwQは問題文を注意深く分析し、与えられた数式が正しくないこと、括弧を追加して正しい式にする必要があることを理解します。 さらに、演算の順序を考慮しながら、括弧をどこに挿入すれば目的の結果が得られるかを検討することが可能です。
また、様々な可能性を段階的に試行するため、 個々の項を括弧で囲む、複数の項をまとめて括弧で囲む、加算と乗算を異なる方法でグループ化するなど、多様な組み合わせを試します。
その過程で、各試行の結果を評価し、目標値との差を分析します。 試行が失敗するたびに、QwQはその結果から学び、次の試行に活かすことが可能です。
最終的にQwQモデルは正しい解答にたどり着きます。 これは、(3 + 4 * 5 + 6)を括弧で囲み、その合計に2と7を掛けることで実現されます。 正解に至るまでには、15回以上の試行と、様々な括弧の組み合わせ、演算の順序の変更などが行われているそうです。
QwQモデルの推論プロセスは、人間の思考プロセスと類似しており、段階的な試行錯誤、深い考察、失敗からの学習といった要素を含んでいます。 このプロセスは、AIの推論能力の進歩を示すものであり、複雑な問題解決においてもAIが有効であることを示唆しています。
QwQ-32Bのライセンス
QwQ-32BはApacheライセンス2.0で提供されています。
Apacheライセンス 2.0は特許ライセンスを含んでいるため、商用利用を含む幅広い使用が可能。再配布や改変時に、元のライセンス条項と表示が求められます。
| 利用用途 | 可否 |
|---|---|
| 商用利用 | ⭕️ |
| 改変 | ⭕️ |
| 配布 | ⭕️ |
| 特許使用 | ⭕️ |
| 私的使用 | ⭕️ |
なお、プログラミング特化LLMのQwen2.5-Coderについて詳しく知りたい方は、下記の記事を合わせてご確認ください。
QwQ-32Bの料金プラン
QwQ-32B自体の利用は基本無料です。モデルの重み(weights)はApache 2.0ライセンスでオープンソース公開されているため、ダウンロードやローカル実行に料金はかかりません。(※1)
公式のWebデモ(Qwen Chat)やHugging Faceデモも無料で公開されており、ユーザー登録さえすれば誰でも無料でモデルを試すことができます。
一方、Alibaba Cloud上で商用サービスとして利用する場合は、従量課金型の料金が設定されています。例えば、Alibaba CloudのModelStudio (DashScope) 経由でQwQ-32BをAPI利用する際は、入力トークン・出力トークンごとに課金されます。
具体的には、QwQ-32Bに相当するモデル(Qwen-Plus, 最大131kトークン文脈長)の場合、入力は1000トークンあたり約$0.0004、出力は1000トークンあたり$0.0012程度に設定されています。
100万トークンあたりに換算すると、入力$0.40+出力$1.20=合計$1.6前後と非常に低コストです。さらに新規ユーザーには、一定の無料枠も提供されており、それを超えた場合に自動的に従量課金が適用される仕組みとなっています。
QwQ-32Bの使い方
ここからは実際にgoogle colaboratoryで実装していきます。
QwQ-32Bにはデモ版が用意されているので、性能をひとまず確認してみたい、という方はデモ版の利用がおすすめです。
ちなみにデモ版では「Please add a pair of parentheses to the incorrect equation: 1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9 = 479, to make the equation true.」というプロンプトにしました。
和訳:不正確な方程式に括弧を追加してください: 1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9 = 479
デモ版の結果はこちら
Okay, so I need to figure out where to add parentheses to this equation to make it equal 479. The original equation is 1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9 = 479. Hmm, right now, without any parentheses, the operations would follow the standard order of operations, which is multiplication before addition. Let me first calculate what the original equation equals so I can see how far off it is from 479.
Starting with the original expression:
1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9
First, do all the multiplications:
23 = 6, 45=20, 67=42, 89=72.
So substituting those in:
1 + 6 + 20 + 42 + 72.
Now add them all up step by step:
1+6 =7,
7+20=27,
27+42=69,
69+72=141.
So the original equation equals 141, but we need it to be 479. That's a big difference. So adding parentheses must change the order of operations to make the result much larger. Parentheses can group parts of the equation to prioritize their evaluation, so maybe grouping some additions before multiplications?
The target is 479, which is way bigger. Let me think about how parentheses can increase the value. Since multiplication is involved, perhaps grouping a larger number in a way that when multiplied, it gives a bigger result. Let's see.
Let me consider different possibilities. Maybe grouping the first few terms?
Option 1: (1 + 2) * 3 + 4 * 5 + 6 * 7 + 8 *9
Calculating this:
(3)*3 + 20 + 42 +72 = 9 + 20 + 42 +72 = 143. Still too low.
Option 2: 1 + (2 * 3 + 4) 5 +67+8*9. Hmm, maybe?
Wait, let me try that step by step. Let's see:
First, (2*3 +4) would be 6+4=10, then multiplied by 5 gives 50.
So the equation becomes 1 + 50 + 42 +72 = 1+50=51, +42=93, +72=165. Still way too low.
Hmm, maybe grouping more terms. Let's see:
What if I group a larger section. Let me think of grouping the first part as (1+2)3+45+67+89. Wait, that was option 1 which gives 143.
Alternatively, perhaps grouping two multiplications together? Like 1 + 2*(3 +4)*5 + ... but that might be overcomplicating.
Alternatively, maybe (1 + 2 * 3 + 4 * 5 + 6 *7 +8)*9? Wait, but that would make the entire left side multiplied by 9, but the equation would then be (1+6+20+42+8)9. Wait, 1+6=7, +20=27, +42=69, +8=77. 779=693, which is way over.
Hmm, maybe not that. Let me think again.
Alternatively, perhaps grouping a part where an addition is done first before a multiplication, leading to a much larger number. For instance, if I can make a term like (something) * (something else) where both are large numbers. Let's see.
Looking at the original expression, maybe grouping the terms after the first few multiplications?
Wait, perhaps if I group 1 + 2*(3 +45 +67 +8*9). Let's see:
First, inside the parentheses: 3 + (45) + (67) + (89). Wait, but without parentheses, that would still do the multiplications first. So inside the big parentheses, it would be 3 +20 +42 +72 = 137. Then multiply by 2: 2137=274. Then add 1 gives 275. Still not enough.
Alternatively, maybe group something like 1 + (2*3 +4)*5 + ... Let's see:
(23 +4) =6+4=10, 5=50. Then the rest: 1 +50 + (67 +89). Wait, but if I group only part of it:
Wait, let me try:
1 + (23 +45 +6*7 +8)*9. Wait, similar to before but different grouping. Let's calculate:
Inside the parentheses: 23=6, 45=20, 67=42, so adding those: 6+20+42+8 = 76. Then times 9 is 684, plus 1? Wait, no, the parentheses would be (23 +45 +67 +8) and then multiplied by 9? Wait, original equation is 1 + [rest]. Wait, maybe:
If the equation is 1 + (23 +45 +6*7 +8)*9, then that would be 1 + (6+20+42+8)*9 =1 + (76)*9= 1 +684=685. Still too big.
Hmm, maybe a different approach. Let me think of the desired result is 479, which is between 400 and 500. Let me see if I can break down 479 into possible multiplicative components.
Alternatively, maybe grouping a longer addition before a multiplication. For example, if I can have a large number added then multiplied.
Suppose I group (1+2)(3+4)(5+6)(7+8)9? Wait, but that might not be allowed because the equation is linear. The original equation is 1 +23+45+67+89. So I can only add parentheses to the existing structure, not rearrange terms. So parentheses can only group existing terms in the sequence.
Wait, the problem says "add a pair of parentheses", so only one pair? Or a pair meaning two parentheses? Maybe the user means adding parentheses in one place, but perhaps more than one pair? Wait, the wording says "a pair of parentheses", which usually means one opening and one closing, so a single pair. Hmm, but maybe two pairs? Let me check the original problem again.
The user says: "Please add a pair of parentheses to the incorrect equation...". So a pair is one pair, so inserting one opening and one closing parenthesis somewhere. So the equation has to have exactly two parentheses added (one pair) to make it correct.
Hmm, so only one pair. So inserting ( and ) somewhere in the equation. Let me think again.
Let me try different placements:
Option: 1 + 2*(3 +4)5 +67+8*9. Let's compute:
First, 3+4=7, multiplied by 2 and 5: 275. Wait, but order matters. It would be 2*(7)*5=70. Then the total would be 1 +70 +42 +72= 1+70=71+42=113+72=185. Still low.
Alternatively, (1 +2)3 +45 +67+89=3*3 +20+42+72=9+20+42+72=143. No.
What if I group the last terms? Like 1 +23 +45 +6*(7+8)*9. Let's see:
Compute 7+8=15, then 615=90, then 9? Wait, no, the grouping would be 6(7+8) which is 615=90, then the rest: 1 +6 +20 +90 +72? Wait, no:
Wait the equation would be 1 +23 +45 +6*(7+8)9. Wait, the original equation is up to +89. Wait, inserting parentheses as 6*(7+8)*9. Let me parse it step by step:
Original expression with parentheses: 1 + 23 +45 +6*(7+8)*9.
Calculating:
First, compute inside the parentheses (7+8)=15. Then 615=90, then multiplied by 9 gives 810? Wait, no. Wait, the expression is 6(7+8)9. Since multiplication is left-associative, so 6(15)9 = 615=90, then 90*9=810. So adding that term:
1 + (23) + (45) + (6*(7+8)*9). So:
1 +6 +20 +810 = 1+6=7+20=27+810=837. That's way over 479.
Hmm, too much. Maybe grouping a smaller part.
What if I group 1 + (23 +4)5 +6789? Wait, but that would require multiple parentheses. Also, the original equation is up to +89, so maybe:
Wait, perhaps grouping (6*7+8)*9? Let's see:
Original equation with parentheses: 1 +23 +45 +67 +89 becomes 1 +23 +45 + (6*7+8)*9.
Compute inside the parentheses: 67=42 +8=50. Then 509=450.
So total equation becomes 1 +6 +20 +450 = 1+6=7+20=27+450=477. Close to 479, but off by 2. Hmm, almost there.
Wait, so 477 vs 479. Maybe close but not quite. Let me check again:
Wait, (6*7 +8)*9:
6*7 is 42, plus 8 is 50, times 9 is 450. Then adding the previous terms:
1 +23=6, so 1+6=7; 45=20, so total so far 7+20=27; then adding the 450 gives 477, plus the remaining terms? Wait no, the original equation after adding parentheses would be:
1 +23 +45 + (67 +8)9. Wait, but in the original, after 67, there's +89. So inserting parentheses around 67 +8 would replace the +89 with (6*7 +8)*9. Wait, perhaps the user wants to keep the structure but insert parentheses. Let me parse it correctly.
Wait, the original equation is:
1 + 2 * 3 + 4 * 5 + 6 * 7 + 8 * 9
If I group the last three terms as (6 * 7 + 8) * 9, then the equation becomes:
1 + 23 +45 + (6*7 +8)*9
Which computes as:
1 +6 +20 + (42+8)9 → 27 + (509) → 27 + 450 = 477. Still 2 short.
Hmm, so maybe that's close but not quite. Let's see where the 2 difference comes from. Maybe grouping a different part.
Alternatively, what if I group (67+89)? Then it would be 42 +72=114. But that's just addition, so multiplying by something? Not sure.
Alternatively, perhaps grouping (1+2)3 +45 +67+89. Wait, we tried that earlier gives 143.
Hmm. Maybe grouping something earlier. Let's see:
If I group (1結果は得られず無限ループに陥ってしまいました。これが前述した循環的な推論パターンですね。
QwQ-32Bのgoogle colaboratoryでの実装方法
公式ページにはGitHubのリンクとHugging Faceのリンクの両方ありますが、Hugging Faceの方がわかりやすいかもしれません。
◼︎Pythonのバージョン
Python3.8以上
◼︎システム RAM
81.8 / 83.5 GB
◼︎GPU RAM
33.8 / 40.0 GB
◼︎ディスク容量
93.7 / 112.6 GB
では実際にgoogle colaboratoryでQwQ-32Bを実装していきます。
まずは必要なライブラリのインストールです。
!pip install transformers accelerate
!pip install torch torchvision torchaudio --index-url https://download.pytorch.org/whl/cu118ライブラリをインストール後、以下のサンプルコードを試してみましょう。
サンプルコードはこちら
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
# モデル名を指定
model_name = "Qwen/QwQ-32B"
# モデルとトークナイザーのロード
model = AutoModelForCausalLM.from_pretrained(
model_name,
torch_dtype=torch.float16, # float16を使用してメモリ使用量を削減
device_map="auto" # 自動的にGPUを活用
)
tokenizer = AutoTokenizer.from_pretrained(model_name)
# プロンプトの設定
prompt = "How many r in strawberry."
messages = [
{"role": "system", "content": "You are a helpful and harmless assistant. You are Qwen developed by Alibaba. You should think step-by-step."},
{"role": "user", "content": prompt}
]
# トークナイザーを使って入力を整形
text = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
# モデルへの入力データを作成
model_inputs = tokenizer([text], return_tensors="pt").to(model.device)
# モデルの推論を実行
generated_ids = model.generate(
**model_inputs,
max_new_tokens=512
)
# 応答を抽出
generated_ids = [
output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]
response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]
print(response)サンプルコードの結果はこちら
Let's see. The word is "strawberry." I need to find out how many times the letter "r" appears in it. Okay, so I'll look at each letter in the word one by one.
First letter: s - that's not r.
Second letter: t - no, not r.
Third letter: r - yes, that's an r.
Fourth letter: a - not r.
Fifth letter: w - not r.
Sixth letter: b - no.
Seventh letter: e - not r.
Eighth letter: r - another r.
Ninth letter: y - not r.
So, I found two r's in "strawberry." Let me just double-check to make sure I didn't miss any.
Starting over: s, t, r, a, w, b, e, r, y. Yep, there's an r in the third position and another one in the eighth position. No other r's in the word.
So, the answer is two. There are two r's in strawberry.
**Final Answer**
\[ \boxed{2} \]LLMが苦手とするstrawberry問題の正答は誤ってしまいました。
性能を高難易度の数学問題と思考実験問題で検証
数学とコーディング能力が非常に高いです。そこで、性能を評価するために、高難易度の数学問題と思考実験問題で検証をしてみます。
今回は、「QwQ-32B-Preview」と「OpenAI-o1」で比較を行います。
高難易度の数学問題
高難易度の数学問題はこちらを与えます。
「円周率が3.05より大きいことを証明せよ。(2003年 東京大学の入試問題より)」
高難易度の数学問題のコードはこちら
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
# モデル名を指定
model_name = "Qwen/QwQ-32B-Preview"
# モデルとトークナイザーのロード
model = AutoModelForCausalLM.from_pretrained(
model_name,
torch_dtype=torch.float16, # float16を使用してメモリ使用量を削減
device_map="auto" # 自動的にGPUを活用
)
tokenizer = AutoTokenizer.from_pretrained(model_name)
# プロンプトの設定
prompt = "円周率が3.05より大きいことを証明せよ。"
messages = [
{"role": "system", "content": "You are a helpful and harmless assistant. You are Qwen developed by Alibaba. You should think step-by-step."},
{"role": "user", "content": prompt}
]
# トークナイザーを使って入力を整形
text = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
# モデルへの入力データを作成
model_inputs = tokenizer([text], return_tensors="pt").to(model.device)
# モデルの推論を実行
generated_ids = model.generate(
**model_inputs,
max_new_tokens=512
)
# 応答を抽出
generated_ids = [
output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]
response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]
print(response)高難易度の数学問題の結果はこちら
円周率が3.05より大きいことを証明せよ、と言われました。まず、円周率とは円の周の長さと直径の長さの比のことですよね。一般的にはπと表記され、約3.14159という値です。なので、3.05より大きいというのは当然のように思えますが、どうやって証明すればいいのか考えなければいけません。
まず、基本的な Approach としては、円の周長と直径の比を計算して、それが3.05より大きいことを示せばいいと思います。しかし、πは無理数なので、正確な値を計算するのは不可能です。だから、近似値を使って証明する必要があるでしょう。perhaps, I can consider a circle with a known diameter and calculate its circumference, then divide the circumference by the diameter to get an approximation of π and show that it's greater than 3.05.
Alternatively, maybe there are some geometric properties or mathematical series that can help me establish a lower bound for π that is greater than 3.05.
Let me think about some historical methods for approximating π. One of the earliest methods is by Archimedes, who used polygons inscribed in and circumscribed around a circle to approximate π. Maybe I can use a similar approach.
So, if I inscribe a regular polygon inside a circle, the perimeter of the polygon will be less than the circumference of the circle. Similarly, if I circumscribe a polygon around the circle, its perimeter will be greater than the circumference. By calculating the perimeters of these polygons and relating them to the diameter, I can get bounds for π.
Let me try this with a hexagon, for simplicity. In a circle with radius r, a regular hexagon inscribed in it has sides of length r, since each side corresponds to one radius.
So, the perimeter of the inscribed hexagon is 6r.
The circumference of the circle is 2πr.
Therefore, 6r < 2πr ⇒ 6 < 2π ⇒ π > 3.
Hmm, that only shows π > 3, but I need to show π > 3.05.
Maybe I need to use a polygon with more sides to get a better approximation.
Let's try with a regular octagon.
For a regular octagon inscribed in a circle of radius r, the side length s can be calculated using思考実験問題
思考実験問題は以下を解いてもらいます。
問1.2人の囚人AとBが逮捕され、別々の部屋で取り調べを受けています。彼らはお互いに連絡を取ることができません。検察官はそれぞれの囚人に以下の選択肢を提示しました。
黙秘: 相手を裏切らず、罪を認めない。
裏切り: 相手を告発し、自分の刑を軽くする。
条件
両者が黙秘した場合、それぞれ軽い罪で 懲役1年。
一方が裏切り、もう一方が 黙秘 した場合、裏切った側は 釈放、黙秘した側は 懲役10年。
両者が裏切りを選んだ場合、それぞれ 懲役5年。こちらは囚人のジレンマと呼ばれる問題です。こちらを検証する問題にしたいと思います。
囚人のジレンマのコードはこちら
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
# モデル名を指定
model_name = "Qwen/QwQ-32B-Preview"
# モデルとトークナイザーのロード
model = AutoModelForCausalLM.from_pretrained(
model_name,
torch_dtype=torch.float16, # float16を使用してメモリ使用量を削減
device_map="auto" # 自動的にGPUを活用
)
tokenizer = AutoTokenizer.from_pretrained(model_name)
# プロンプトの設定
prompt = """2人の囚人AとBが逮捕され、別々の部屋で取り調べを受けています。彼らはお互いに連絡を取ることができません。検察官はそれぞれの囚人に以下の選択肢を提示しました。
黙秘: 相手を裏切らず、罪を認めない。
裏切り: 相手を告発し、自分の刑を軽くする。
条件
両者が黙秘した場合、それぞれ軽い罪で 懲役1年。
一方が裏切り、もう一方が 黙秘 した場合、裏切った側は 釈放、黙秘した側は 懲役10年。
両者が裏切りを選んだ場合、それぞれ 懲役5年。"""
messages = [
{"role": "system", "content": "You are a helpful and harmless assistant. You are Qwen developed by Alibaba. You should think step-by-step."},
{"role": "user", "content": prompt}
]
# トークナイザーを使って入力を整形
text = tokenizer.apply_chat_template(
messages,
tokenize=False,
add_generation_prompt=True
)
# モデルへの入力データを作成
model_inputs = tokenizer([text], return_tensors="pt").to(model.device)
# モデルの推論を実行
generated_ids = model.generate(
**model_inputs,
max_new_tokens=2512
)
# 応答を抽出
generated_ids = [
output_ids[len(input_ids):] for input_ids, output_ids in zip(model_inputs.input_ids, generated_ids)
]
response = tokenizer.batch_decode(generated_ids, skip_special_tokens=True)[0]
print(response)囚人のジレンマの結果はこちら
これは有名な囚人 dilemma ですね。2人の囚人AとBが、それぞれ別々の部屋で取り調べを受けている状況で、お互いの行動が不透明なまま、自分の選択を迫られます。選択肢は「黙秘」か「裏切り」のどちらかで、それぞれの組み合わせによって罰則が異なります。
まず、状況を整理しておきましょう。
- 両方が黙秘を選ぶ場合:それぞれ懲役1年。
- 一方が裏切り、もう一方が黙秘の場合:裏切った側は釈放、黙秘した側は懲役10年。
- 両方が裏切りを選ぶ場合:それぞれ懲役5年。
このゲーム理論の問題では、お互いの利害が対立していて、協力(黙秘)と裏切りの選択が複雑になります。特に、お互いにコミュニケーション不能な状況では、信頼が試されます。
まず、個人として最善の選択は何かを考えましょう。
例えば、囚人Aの立場で考えます。AはBの行動がわからないので、2つのケースを考える必要があります:Bが黙秘か、Bが裏切るか。
1. Bが黙秘を選ぶ場合:
- Aも黙秘:1年刑務所。
- Aが裏切る:釈放。
2. Bが裏切る場合:
- Aが黙秘:10年刑務所。
- Aも裏切る:5年刑務所。
ここで、AはBの行動を予測不能なので、自身の選択が最も不利にならないように行動する必要があります。
まず、Bが黙秘を選ぶと仮定した場合、Aが裏切った方が有利です(釈放 vs. 1年)。
同じように、Bが裏切るだろうと仮定した場合、Aが黙秘选择すると10年 Becomes、裏切った方が5年 Becomes、なので裏切った方が有利です。
つまり、どちらのケースでも、Aが裏切る方がより良い結果 becomes。これはBも同じ立場にありますので、同じように考え、裏切る方向に傾くでしょう。
しかし、両方が裏切る选择すると、それぞれ5年 Becgoogle colaboratoryだと処理速度がかなり遅いので、こちらはvast.aiを使って実装をしました。コード自体はgoogle colaboratoryでもそのまま使えます。
トークン数の関係で途中で切れてしまいましたが、適切に思考できているように思います。
なお、数学の関連情報を学習データに用いているQwen2-Mathについて詳しく知りたい方は、下記の記事を合わせてご確認ください。

QwQ-32Bの活用事例
最後にQwQ-32Bの活用事例をご紹介します!
1.他推論フレームワークを併用して実行の高速化
「QwQ-32B」をSGlangなどの推論フレームワークと併用することで、さらに推論速度が向上することが分かりますね。
従来は、パフォーマンス向上にGPU増設が必須でしたが、フレームワークの工夫により、ハードウェアコストを抑えつつ、高速化を実現できるのは画期的です。
今後、このような効率化が進めば、個人レベルでも高性能モデルを手軽に利用できるようになりそうです。
2.他モデルとの比較
上記のYouTube動画では「QwQ-32B」と「DeepSeek-R1」を比較し、無料で高機能なモデルを手軽にローカル実行できる優位性が紹介されています。
関数呼び出しの柔軟さやアーティファクト生成能力の高さも具体的にデモされており、実用性が明確に伝わります。
他モデルとの比較によって性能を客観的に比較し、大変参考になる内容ですね。
3.プログラミング支援
従来モデルでも、コード生成や簡単な不具合修正は可能でしたが、「QwQ-32B」は原因の特定が難しい複雑なエラーの診断にも役立ち、「このレベルのAIが無料で使えるとは信じられない」と述べられています。※2
「QwQ-32B」は単なるコード生成や初歩的な修正にとどまらず、原因特定が困難な高度なエラー診断にも対応できる点が強みだと分かりますね。
特に、プログラミング初心者の方や個人開発者にとっても、無料で利用できるのはメリットと言えると思います。
開発効率を大幅に向上することができるため、今後、ますます幅広い層のユーザーに利用されそうです。
まとめ
本記事では、QwQ-32Bについて詳しく解説し、google colaboratoryでの実装方法を紹介しました。高性能なLLMが次から次へと登場していきますが、それぞれのモデルの特性を理解して、活用していくのがいいですね。
QwQ-32Bは数学とコーディングに特化しているモデルなので、特に機械学習などをコーディングする方は重宝するモデルになるのではないでしょうか。
ぜひ本記事を参考に実装してみてください!
最後に
いかがだったでしょうか?
LLMを活用することで、複雑な問題に挑み、先進的なAI技術をビジネスに活用するための可能性を広げられます。次の一歩として、生成AIがビジネス課題解決にどのように役立つか具体的に検討してみませんか?
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、大規模言語モデル(LLM)を対象に、言語理解能力、生成能力、応答速度の各側面について比較・検証した資料も配布しております。この機会にぜひご活用ください。







