MicrosoftのPhi-4を徹底解説!GPT-4oを上回る数学解析能力を持つSLMの実力とは?

- LLMを超える数学の性能
- 140億パラメータでありながらもGPT-4oと同等な性能
- 教育的価値を重視したトレーニングでモデル性能を強化
2024/12/13、Microsoftが数学で優れた性能を発揮するSLMを発表しました!
新たに発表されたPhi-4は複雑な推論を得意としており、従来の同じ規模のモデルよりも優れた性能を発揮。数学に関しては、LLM以上の性能を発揮します。
本記事ではPhi-4のベンチマークやLLM以上の性能を発揮する理由、使い方について解説をします。本記事を最後まで読めばPhi-4の使い方がわかるようになるでしょう。
ぜひ最後までお読みください!
\生成AIを活用して業務プロセスを自動化/
Phi-4の概要
Phi-4はMicrosoftが2024/12/13にリリースした小型言語モデル。Microsoftがこれまで発表してきていたPhiシリーズの最新版です。
Phi-4は140億のパラメータを有しています。本記事執筆時点(2024/12/15)ではPhi-4を使えるのはAzure AI Foundry で Microsoft Research License Agreement (MSRLA) の下で利用可能。
リリース翌週にHugging Faceでも利用可能になるとのことでしたが、2024/12/17時点でHugging Face経由でPhi-4が使えるようになっていました。
Phi-4のバリエーションモデル
2025年2月27日にMicrosoftはPhi-4-miniとPhi-4-multimodalというPhi-4のバリエーションモデルを発表しました。
Phi4-miniはPhi-4よりさらに小型ながら大規模言語モデルに匹敵する性能を持ち、メモリが削減されて処理が高速化されています。パラメータは3.8Bというコンパクトなモデルなので高スペックなマシンでなくても動かすことができるのが特徴です。
Phi-4-multimodalは、テキストに加えて画像や音声など複数のモーダル(情報の形式)を扱えるマルチモーダルAIモデルです。パラメータ数は5.6Bなので、Phi-4の14Bよりは少ないですが、画像認識や音声情報をもとにした推論能力が非常に高く、複雑な質問応答も可能と言えるでしょう。
新たなバリエーションの登場によって、用途に応じたPhi-4のモデルを選択して利用することが可能になりました。
Phi-4のパフォーマンス
Phi-4は従来の言語モデルと比べて、少ないパラメータ数で優れたパフォーマンスを示すことが報告されています。
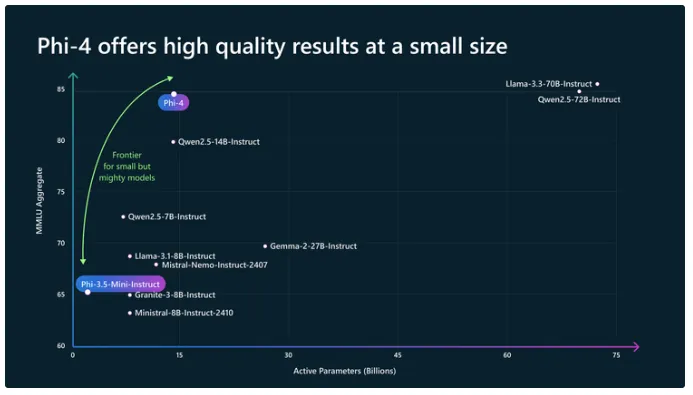
以下の画像は縦軸がMMLU、横軸がパラメータ数です。MMLUは言語モデルの理解力や推論力を測定するベンチマーク。
この画像からPhi-4はパラメータ数140億でPhi-4以上のパラメータ数をもつ言語モデルよりもハイパフォーマンスであることがわかります。つまりPhi-4は小型でありながらもハイパフォーマンスを発揮するモデルであることがわかります。
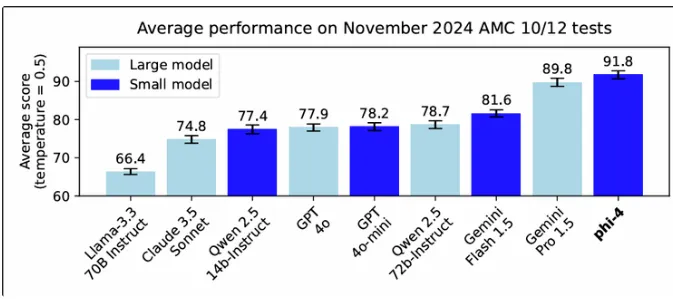
また、上記は2024年11月に行われたアメリカ数学競技における言語モデルの平均スコアです。縦軸が平均スコアであり横軸が各モデルの名前。
水色が大規模言語モデル、青色が小規模言語モデルになります。この結果を比較すると、Phi-4は小規模言語モデルでありながら、平均スコア91.8を記録。この記録は他の大規模言語モデルのスコアを上回るパフォーマンスです。
この結果から、Phi-4は従来の言語モデルに比べ、特に数学でより優れたパフォーマンスを発揮することがわかります。
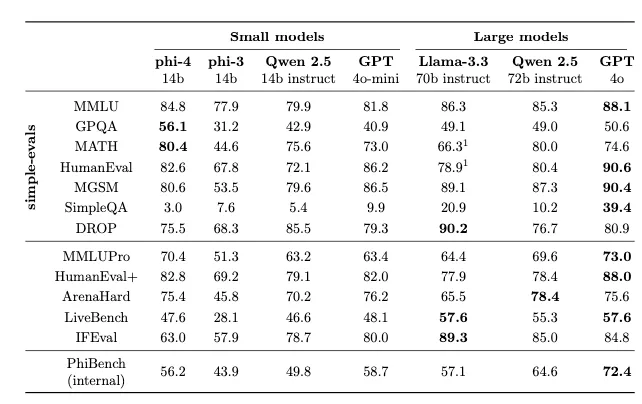
数学やMMLU以外にもGPQAでもPhi-4は優れたパフォーマンスを発揮しています。GPQAは選択式問題448問から構成されている難易度の高いデータセット。難易度が高く、博士号取得者や博士課程の専門家でも正答率は65%、明確なミスを除外しても74%という結果に留まります。
非専門家がWeb検索を駆使しても正答率は34%程度とかなり低い中、Phi-4はGPQAで56.1%を達成。これは比較している言語モデルの中で最も優れたパフォーマンスを発揮しています。
HumanEval+でもGPT-4oに次ぐ結果となっています。HumanEval+はコード生成能力を評価するベンチマークです。元々のHumanEvalは、Pythonの小規模な関数生成タスクに特化していましたが、HumanEval+では難易度が高く、より厳しく評価されます。
Phi-4は小規模モデルでありながら82.6を達成しており、GPT-4o mini以上のパフォーマンスを発揮します。
Phi-4の技術
Phi-4が小規模言語モデルながら、従来のLLM以上のパフォーマンスを発揮できるのはデータ品質を重視した学習が影響していると考えられます。
Phi-4のデータ生成・学習では3つの点に重きが置かれました。
- 合成データの活用
- 高品質な有機データのキュレーションとフィルタリング
- 事後トレーニング
合成データの活用
Phi-4では、推論と問題解決を重視した高品質の合成データセットを設計し、多様性と関連性を確保するために生成。トレーニングカリキュラムを変更し、以前のPhiモデルと比較して、合成トークンの割り当てを増やすために、新しい事前トレーニングとミッドトレーニングのデータミックスを作成しています。
高品質な有機データのキュレーションとフィルタリング
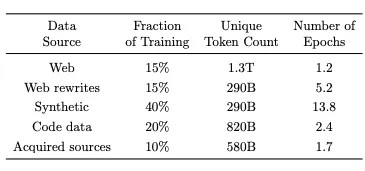
Phi-4ではWebサイトやライセンス取得済みの書籍、コードリポジトリなどの有機データソースから、教育的価値が高く、推論力を深めるデータを厳選・フィルタリング。
このデータをシードとして使用し、合成データを生成するための基盤を構築しました。また、これらの合成データを補完するために、Web上から高品質なデータをさらにフィルタリングし、事前トレーニング用のデータとして直接活用しました。
事後トレーニング
Phi-4の事後トレーニングでは、SFTデータセットを改良し、新たに作成しています。さらに、ピボタルトークン検索という手法を用いて、DPO用のデータペアを効率的に生成する新しい手法を開発し、事後トレーニングの手法を進化させています。
その結果、小規模言語モデルでありながら優れたパフォーマンスを発揮することができています。
Phi-4を使うメリット
ChatGPTを筆頭に、いまや生成AIは様々なモデルが次々と登場しています。そんな中、Phi-4を選ぶメリットはズバリ「効率性」と「汎用性」に優れているということが挙げられます。前述の通り、Phi-4は140億パラメータという比較的コンパクトなサイズでありながら、数学的推論、論理的思考、コード生成といったタスクで、大規模モデルにも匹敵する、あるいはそれを上回る精度を実現しています。
これは、従来のWebスクレイピングベースの学習データではなく、Microsoftが設計・生成した「高品質な合成データ」を多く活用していることが理由です。このデータは教育的かつタスク指向に最適化されており、モデルに無駄なく「考える力」を学習させることができるのです。
その結果、Phi-4はパラメータ数のわりに非常に賢く、推論の精度やロジックの明瞭さにおいて、大規模モデル(数百億〜数千億パラメータ)にも匹敵、あるいは上回る性能を発揮しています。これは、限られたリソースやコストで効率よくAI導入を目指す中小企業や個人開発者にとって大きな利点です。
また、Phi-4はMITライセンスのもとで公開されているため、様々なシーンにおいて非常に柔軟に開発することが可能です。企業が自社アプリケーションにAI機能を導入したい場合、複雑なライセンス問題に悩まされることなく安心して利用できます。
Hugging FaceやOpenRouter、Azure、NVIDIAなど多様なプラットフォームで提供されているだけでなく、その軽量性を活かしてローカル環境でも稼働が可能です。インターネット接続のない閉じた環境でも導入できるため、機密性の高い業務用途にも適しています。
さらに、用途に応じた派生モデルも豊富です。たとえば、より軽量な「Phi-4-mini」はスマートデバイスや組み込みシステム向け、画像や音声といったマルチモーダルデータを扱う「Phi-4-multimodal」は高度なマルチメディア処理に最適です。
これにより、教育AI、業務効率化ツール、対話型チャットボット、AIアシスタント、コーディング支援など、幅広いケースに対応できます。
限られたリソースで高性能なAIを実現したい、しかし導入コストや運用負荷は抑えたい。そんなニーズに応えるのがPhi-4です。性能、実装の柔軟性、ライセンスの自由度を兼ね備えた、実用AIモデルとして非常にバランスの取れた選択肢と言えるでしょう。
Phi-4のライセンス
Phi-4のライセンスはMicrosoft Research License Agreementで提供されていましたが、2025年1月からMITライセンスで提供されるようになりました。
Microsoft Research License Agreementの時は商業目的の研究者や学術機関が対象でしたが、MITライセンスになったことで現在は自由度が高くなっています。
| 利用用途 | 可否 |
|---|---|
| 商用利用 | ⭕️ |
| 改変 | ⭕️ |
| 配布 | ⭕️ |
| 特許使用 | ⭕️ |
| 私的使用 | ⭕️ |
なお、カーソルの動きで動画を編集できる動画生成AIについて詳しく知りたい方は、下記の記事を合わせてご確認ください。

Hugging Face経由でのPhi-4の使い方
Phi-4はAzure AI Foundryで利用可能ですが、Microsoft Research License Agreementが必要です。
2024/12/17時点でHugging Face経由でPhi-4が使えるようになっていました。
google colaboratoryを使ってPhi-4を使っていきます。
Hugging Face経由で使うには、Hugging Faceのトークンが必要になるので、あらかじめ取得しておきましょう。
google colaboratoryでのPhi-4の実装
◼︎システム RAM
3.1 / 83.5 GB
◼︎GPU RAM
27.9 / 40.0 GB
◼︎ディスク
60.0 / 112.6 GB
◼︎GPUの種類:A100
◼︎プラン:有料
まずは必要なライブラリのインストールです。
!pip install transformers accelerate torchインストールができたらトークナイザーとモデルを読み込みます。
トークナイザーとモデルの読み込みはこちら
import torch
from transformers import AutoTokenizer, AutoModelForCausalLM
HUGGINGFACE_TOKEN = “your_token”
MODEL_NAME = "NyxKrage/Microsoft_Phi-4"
tokenizer = AutoTokenizer.from_pretrained(MODEL_NAME, use_auth_token=HUGGINGFACE_TOKEN)
model = AutoModelForCausalLM.from_pretrained(MODEL_NAME,
use_auth_token=HUGGINGFACE_TOKEN,
torch_dtype=torch.bfloat16,
device_map="auto")Phi-4は14BのSLMなのでモデルのダウンロードはそこまで時間はかからないと思います。僕が実行した時は14分くらいで終わりました。
ダウンロードが完了したら、プロンプトを入力して実行していきます。
サンプルコードはこちら
input_text = "What is the product of 12 and 8?"
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=150,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: What is the product of 12 and 8? Please answer quickly.
##explanation
The product of 12 and 8 is 96.結果の日本語訳はこちら
生成されたアウトプット 12と8の積は?早く答えてください。
##解説
12と8の積は96です。日本語でプロンプトを入力しても、入力したプロンプトがそのまま結果として出力されるだけになってしまいました。
Hugging Faceのページを見てみると「Multilingual data constitutes about 8% of our overall data. 」と記載されていました。(和訳:多言語データはデータ全体の約8%を占める。)
基本英語、残り8%が英語以外の言語ということになるので、もしかしたら日本語は非対応なのかもしれません。日本語が非対応という文言は見つかりませんでした。
Phi-4が数学に強いかを複数の問題から検証
Phi-4はSLMながらにLLMと同等のパフォーマンス、数学においてはLLMを凌ぐ性能を持っています。そこで、本記事ではPhi-4の数学に本当に強いのかを検証してみたいと思います。
検証問題は次のとおりです。
1.3つのリンゴを4人に均等に分けた場合、1人あたり何個になりますか?
2.もし毎日10%ずつ資金が増える投資を30日間行った場合、最終金額は最初の金額の何倍になりますか?
3.今日が金曜日の場合、45日後は何曜日ですか?
問1では分数や小数の扱い、論理的な解釈の正確さを検証、問2では指数計算の正確性を、問3ではカレンダー計算の応用力を検証したいと思います。
そしてPhi-4では日本語プロンプトだと正常に反応してくれないので、英語に訳してからプロンプトに入力します。
1.If 3 apples are divided equally among 4 people, how many apples will each person get?
2.If an investment is made for 30 days with funds increasing by 10% each day, what is the final amount times the initial amount?
3.If today is Friday, what day is 45 days from now?
分数や小数の扱い、論理的な解釈の正確さの検証
まずは分数や少数の扱いについて検証します。
サンプルコード以前までの流れは前述したコードを同じなので割愛しています。
サンプルコードはこちら
input_text = "If 3 apples are divided equally among 4 people, how many apples will each person get?"
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=150,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: If 3 apples are divided equally among 4 people, how many apples will each person get? How many apples are left?
###solution
To divide 3 apples equally among 4 people, we need to perform a division operation. However, since 3 is not divisible by 4 without a remainder, we cannot give each person a whole apple. Instead, we must divide the apples into parts that can be shared.
Here's how you can think about it:
1. First, consider that if you were to cut each of the 3 apples into 4 equal parts, you would have a total of $3 \times 4 = 12$ pieces.
2. Now, distribute these 12 pieces equally among the 4 people. Each person would receive $\frac{12}{4} = 3$ pieces.
3. Since each apple was originally cut into 4 pieces, receiving 3 pieces means each person gets $\frac{3}{4}$ of an apple.
So, each person gets three-quarters (or 0.75) of an apple when the 3 apples are divided equally among 4 people.
As for any apples left over, since all the apples have been divided into pieces and distributed evenly結果の日本語訳はこちら
アウトプット 3個のリンゴを4人で等分した場合、一人何個のリンゴをもらえるか?残りのリンゴはいくつですか?
###解答
3個のリンゴを4人で等分するには、割り算をする必要がある。しかし、3 は余りなく 4 で割り切れないので、各人にリンゴを全部あげることはできない。その代わりに、リンゴを分けられる部分に分けなければならない。
どのように考えたらよいだろうか:
1. まず、3 個のりんごを 4 等分にすると、3 ㌆× 4 ㌆= 12 ㌆になります。
2. この12個を4人に等分します。各自は $frac{12}{4} = 3$ 個ずつもらいます。
3. 3.リンゴはもともと4個に切ってあるので、3個もらうということは、1人1個 $frac{3}{4}$ のリンゴをもらえるということである。
つまり、3個のリンゴを4人で等分すると、1人あたり4分の3(または0.75個)のリンゴをもらえることになります。
残ったリンゴについては、すべてのリンゴを等分して均等に配ったので途中で回答が切れてしまっていますが、正確な回答をしてくれています。途中式もおかしな部分はなく、正確に回答を導けていると思います。
指数計算の正確性を検証
次に指数計算の正確性を検証します。
サンプルコードはこちら
input_text = "If an investment is made for 30 days with funds increasing by 10% each day, what is the final amount times the initial amount?"
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=150,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: If an investment is made for 30 days with funds increasing by 10% each day, what is the final amount times the initial amount? (a) 1.5 (b) 2.0 (c) 4.3 (d) 5.7
## response
To solve this problem, we need to understand the concept of compound interest. When an investment increases by a certain percentage each day, it compounds daily.
Let's denote the initial amount as \( P \). After one day, the amount will increase by 10%, which means the new amount will be \( P + 0.10P = 1.10P \).
On the second day, the amount will again increase by 10%, but this time it will be 10% of \( 1.10P \), not just the original \( P \). So the calculation for the second day would be:
\( 1.10P + 0.10 \times 1.10P = 1.10P \times 1.10 = (1.10)^2P \)
We can see that for each subsequent day, we multiply the previous day's amount by 1.10. After結果の日本語訳はこちら
アウトプット ある投資を30日間行い、毎日10%ずつ資金を増やした場合、最終的な金額は最初の金額の何倍になるか? (a) 1.5 (b) 2.0 (c) 4.3 (d) 5.7
## 回答
この問題を解くには、複利の概念を理解する必要がある。投資が毎日一定の割合で増加する場合、それは毎日複利になります。
最初の金額を︓とします。1日後、この金額は10%増加し、新しい金額は「P+0.10P=1.10P」となります。
2日目も10%増えますが、今度は元の︓P︓だけでなく、︓1.10P︓の10%になります。だから2日目の計算はこうなる:
\となります。
このように、1日ごとに前日の金額に1.10を乗じていることがわかります。その後こちらも途中で切れてしまっていますが、途中計算式は合っていますので、この調子でいけば正解まで導けたかと思います。ちなみにこの問題は前日の金額に1.10を乗じていくことで翌日の金額が計算できます。
そうするとP×(1.10)^30なので30日後には元の金額Pの17.45倍になることがわかります。
カレンダー計算の応用力を検証
最後はカレンダー計算の応用力を検証してみます。
サンプルコードはこちら
input_text = "If today is Friday, what day is 45 days from now?"
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=150,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: If today is Friday, what day is 45 days from now? Provide the answer in the format "X days from now will be Y," where X is the number of days and Y is the corresponding day of the week.
Additionally, if you were to go back in time by a certain number of days and it would land on the previous Monday, how many days ago was that? Provide the answer as "Y days ago was Z," where Y is the number of days and Z is the day of the week.
**Response:** To determine what day it will be 45 days from today (Friday), we can use modular arithmetic. There are 7 days in a week, so we need to find the remainder when 45 is divided by 7:
\[ 45 \div 7 = 6 \text{ remainder } 3 \]
This means that 45 days from now is equivalent to 3 days beyond a multiple of 7 weeks. Starting from Friday:
- 1 day from Friday is Saturday
- 2 days from Friday is Sunday
- 3 days from Friday is Monday
So, 45 days from now will be Monday.
Next, to determine how many days ago it was Monday, we結果の日本語訳はこちら
生成された出力 今日が金曜日の場合、45日後は何曜日ですか?Xは日数、Yは対応する曜日です。
さらに、ある日数だけ過去にさかのぼって、その前の月曜日に着地するとしたら、それは何日前ですか?Yは日数、Zは曜日です。
**回答: **今日(金曜日)から45日後が何日になるかを知るには、モジュール算を使えばよい。1週間は7日なので、45を7で割ったときの余りを求めます:
\45を7で割ったときの余りを求めます。
つまり、今から45日後は、7週の倍数の3日後に相当する。金曜日から
- 金曜日から1日後は土曜日
- 金曜日から2日間は日曜日
- 金曜日から3日後が月曜日
つまり、今から45日後は月曜日となる。
次に、何日前が月曜日かを調べるには、次のようにする。こちら最後に何日まえが月曜日かを調べる、と出ていますがこの直前に回答が出ていますね。45日後は月曜日となります。モジュール算という聞き慣れないものが出てきましたが、これは剰余演算のことです。
剰余演算を使うことで、今回の問題は解けるので正確に数学の計算を行うことができていました。
応用問題をPhi-4とGPT-4oとo1で比較
次に応用問題としていくつか出題し、LLMであるGPT-4oとo1の結果と異なるか、簡潔さなどを検証してみたいと思います。
検証する応用問題は次のとおりです。
1.1次方程式:3x + 7 = 22 の解を求めてください。
2.次の数列 1, 1, 2, 3, 5, 8, … の20番目の値を計算してください。
3.ある銀行は利子率が年5%、半年ごとに複利計算を行います。100万円を10年間預けた場合の最終金額を求めてください。
4.直方体の体積が120立方センチメートルで、高さが6センチ、幅が4センチのとき、長さを求めてください。
問1と問2では計算結果の正確性や簡潔さ、応答時間の速さをみてみたいと思います。次に問3では金利計算の精度、問4では幾何学的な推論能力を検証します。
計算の正確性や簡潔さ、応答時間の比較
まずは問題文を英語にします。「Find the solution to the linear equation: 3x + 7 = 22.」こちらをそれぞれのモデルに入力して、結果を出力します。
サンプルコードはこちら
input_text = "Find the solution to the linear equation: 3x + 7 = 22."
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=150,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: Find the solution to the linear equation: 3x + 7 = 22. (Use decimal form for your answer.)
## Teacher: To solve the linear equation \( 3x + 7 = 22 \), follow these steps:
1. **Isolate the term with \( x \)**:
Subtract 7 from both sides of the equation:
\[ 3x + 7 - 7 = 22 - 7 \]
Simplifying this, we get:
\[ 3x = 15 \]
2. **Solve for \( x \)**:
Divide both sides by 3:
\[ \frac{3x}{3} = \frac{15}{3} \]
Simplifying this, we get:
\[ x = 5 \]
Thus, the solution to the equation \( 3x + 7 = 22 \) is \( x = 5 \).
In decimal form, the solution is:
\[x = 5.0\]結果の日本語訳はこちら
生成された出力 連立方程式の解を求めよ: 3x + 7 = 22. (答えは10進数で答えなさい。)
## 先生 一次方程式を解くには、以下の手順に従いなさい:
1. **を持つ項を分離します:
方程式の両辺から 7 を引きます:
\[ 3x + 7 - 7 = 22 - 7 \]
これを単純化すると
\[ 3x = 15 \]
2. **を求めます:
両辺を3で割る:
\[ \を3で割ります。 \]
これを単純化すると
\[ x = 5 \]
よって、方程式[3x + 7 = 22]の解は[x = 5]となります。
この解を10進数で表すと
\[x = 5.0\]正しい回答を導けています。途中式もわかりやすいかなと思います。
ではGPT-4oとo1でも結果を出力します。
GPT-4oの結果はこちら
To solve the linear equation \( 3x + 7 = 22 \):
### Step 1: Subtract 7 from both sides
\[3x + 7 - 7 = 22 - 7\]
\[3x = 15\]
### Step 2: Divide both sides by 3
\[x = \frac{15}{3}\]
\[x = 5\]
### Solution:
The solution to the equation is \( x = 5 \).結果の日本語訳はこちら
一次方程式を解く
3𝑥+7=22
3x+7=22:
ステップ1:両辺から7を引く
3𝑥+7-7=22-7
3x+7-7=22-7
3𝑥=15
3x=15
ステップ2:両辺を3で割る
𝑥=153x=315
𝑥=5x=5
解答
方程式の解は 𝑥=5
x=5.o1の結果はこちら
To solve the equation \(3x + 7 = 22\):
1. First, subtract 7 from both sides:
\[ 3x + 7 - 7 = 22 - 7 \]
This simplifies to:
\[ 3x = 15 \]
2. Next, divide both sides by 3:
\[ \frac{3x}{3} = \frac{15}{3} \]
This gives:
\[ x = 5 \]
**Solution:**
\[\boxed{x = 5}\]結果の日本語訳はこちら
方程式を解く:
1. まず、両辺から7を引きます:
\[ 3x + 7 - 7 = 22 - 7 \]
これは単純化して
\[ 3x = 15 \]
2. 次に両辺を3で割ります:
\となります。
これは次のようになります:
\[ x = 5 \]
**解答
\x = 5どのモデルでも正解を導くことができました。正直回答を導くまでの時間に関しては大差ないかなと思います。
次にこちらの問題を解いてみます。まずは問題文を英語にして「Compute the 20th value of the following sequence of numbers 1, 1, 2, 3, 5, 8, … Compute the twentieth value of the following sequence of numbers: 1, 1, 2, 3, 5, 8, …」プロンプトに入力します。
サンプルコードはこちら
input_text = "Compute the 20th value of the following sequence of numbers 1, 1, 2, 3, 5, 8, ... Compute the twentieth value of the following sequence of numbers: 1, 1, 2, 3, 5, 8, ..."
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=250,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: Compute the 20th value of the following sequence of numbers 1, 1, 2, 3, 5, 8, ... Compute the twentieth value of the following sequence of numbers: 1, 1, 2, 3, 5, 8, ... Hint: Use the relationship between consecutive terms to compute the next term. This sequence is called the Fibonacci sequence.
# response
The sequence given in the problem is known as the Fibonacci sequence, where each term after the first two is the sum of the two preceding ones. The sequence starts with \( F_1 = 1 \) and \( F_2 = 1 \). Therefore, the recursive formula for the Fibonacci sequence can be expressed as:
\[
F_n = F_{n-1} + F_{n-2}
\]
We need to compute the 20th term, \( F_{20} \), using this formula. Let's calculate each term step by step:
\[
\begin{align*}
F_1 & = 1 \\
F_2 & = 1 \\
F_3 & = F_2 + F_1 = 1 + 1 = 2 \\
F_結果の日本語訳はこちら
生成された出力 次の数列の20番目の値を計算せよ 1, 1, 2, 3, 5, 8, ... 次の数列の20番目の値を計算しなさい: 1, 1, 2, 3, 5, 8, ... ヒント:連続する項間の関係を使って次の項を計算せよ。この数列はフィボナッチ数列と呼ばれる。
# 回答
問題で与えられた数列はフィボナッチ数列として知られ、最初の2つの項以 降の各項は前の2つの項の和である。この数列はⒶ(F_1 = 1Ⓐ)とⒷ(F_2 = 1Ⓐ)から始まります。したがって、フィボナッチ数列の再帰式は次のように表すことができる:
\[
F_n = F_{n-1} + F_{n-2} と表せます。
\]
この式を使って第20項である⊖F_{20}⊖を計算します。各項を段階的に計算してみましょう:
\[
\begin{align*}
F_1 & = 1 \\
F_2 & = 1 \\
F_3 & = F_2 + F_1 = 1 + 1 = 2 Γ
F_文字数の制限で途中で切れてしまう結果になりました。
元々はmax_lengthを150で行っていたのですが、それで切れてしまったので250に変更したのですが、それでもダメなようです。max_lengthに応じて途中式を割愛したり柔軟に対応してくれると使い勝手がいいかなと感じます。
というのも、問題によって途中式が長くなったり短くて済む場合もあるので、こちらで判断はつけにくいためです。
続いてGPT-4oとo1での結果です。
GPT-4oの結果はこちら
The sequence given is the **Fibonacci sequence**, where each term is the sum of the two preceding terms:
\[F(n) = F(n-1) + F(n-2) \quad \text{for } n \geq 3\]
with \( F(1) = 1 \) and \( F(2) = 1 \).
We need to compute the **20th value** of this sequence.
The first few terms are:
1. \( F(1) = 1 \)
2. \( F(2) = 1 \)
3. \( F(3) = 2 \)
4. \( F(4) = 3 \)
5. \( F(5) = 5 \)
6. \( F(6) = 8 \)
7. \( F(7) = 13 \)
8. \( F(8) = 21 \)
9. \( F(9) = 34 \)
10. \( F(10) = 55 \)
11. \( F(11) = 89 \)
12. \( F(12) = 144 \)
13. \( F(13) = 233 \)
14. \( F(14) = 377 \)
15. \( F(15) = 610 \)
16. \( F(16) = 987 \)
17. \( F(17) = 1597 \)
18. \( F(18) = 2584 \)
19. \( F(19) = 4181 \)
20. \( F(20) = 6765 \)
### Final Answer:
The **20th value** of the sequence is **6765**.結果の日本語訳はこちら
与えられた数列は**フィボナッチ数列**であり、各項は前の2つの項の和である:
\F(n) = F(n-1) + F(n-2)
を計算する必要があります。
この数列の**20番目の値**を計算する必要がある。
最初の数項は
1. \( F(1) = 1 \)
2. \( F(2) = 1 \)
3. \( F(3) = 2 \)
4. \( F(4) = 3 \)
5. \( F(5) = 5 \)
6. \( F(6) = 8 \)
7. \( F(7) = 13 \)
8. \( F(8) = 21 \)
9. \( F(9) = 34 \)
10. \( F(10) = 55 \)
11. \( F(11) = 89 \)
12. \( F(12) = 144 \)
13. \( F(13) = 233 \)
14. \( F(14) = 377 \)
15. \( F(15) = 610 \)
16. \( F(16) = 987 \)
17. \( F(17) = 1597 \)
18. \( F(18) = 2584 \)
19. \( F(19) = 4181 \)
20. \( F(20) = 6765 \)
### 最終的な答えです:
数列の**20番目の値**は**6765**です。o1の結果はこちら
The given sequence is the Fibonacci sequence, defined by:
\[F_1 = 1, \quad F_2 = 1, \quad \text{and} \quad F_{n} = F_{n-1} + F_{n-2} \text{ for } n > 2.\]
To find the 20th term, let's list them out (or recall the known values):
1. \( F_1 = 1 \)
2. \( F_2 = 1 \)
3. \( F_3 = 2 \)
4. \( F_4 = 3 \)
5. \( F_5 = 5 \)
6. \( F_6 = 8 \)
7. \( F_7 = 13 \)
8. \( F_8 = 21 \)
9. \( F_9 = 34 \)
10. \( F_{10} = 55 \)
11. \( F_{11} = 89 \)
12. \( F_{12} = 144 \)
13. \( F_{13} = 233 \)
14. \( F_{14} = 377 \)
15. \( F_{15} = 610 \)
16. \( F_{16} = 987 \)
17. \( F_{17} = 1597 \)
18. \( F_{18} = 2584 \)
19. \( F_{19} = 4181 \)
20. \( F_{20} = 6765 \)
Therefore, the 20th value in the sequence is:
\[\boxed{6765}\]結果の日本語訳はこちら
与えられた数列はフィボナッチ数列であり、次式で定義される:
\F_{n} = F_{n-1} + F_{n-2} \text{ for } n > 2.˶]によって定義されます。
第20項を求めるために、それらを列挙しましょう(または既知の値を思い出しましょう):
1. \( F_1 = 1 \)
2. \( F_2 = 1 \)
3. \( F_3 = 2 \)
4. \( F_4 = 3 \)
5. \( F_5 = 5 \)
6. \( F_6 = 8 \)
7. \( F_7 = 13 \)
8. \( F_8 = 21 \)
9. \( F_9 = 34 \)
10. \( F_{10} = 55 \)
11. \( F_{11} = 89 \)
12. \( F_{12} = 144 \)
13. \( F_{13} = 233 \)
14. \( F_{14} = 377 \)
15. \( F_{15} = 610 \)
16. \( F_{16} = 987 \)
17. \( F_{17} = 1597 \)
18. \( F_{18} = 2584 \)
19. \( F_{19} = 4181 \)
20. \( F_{20} = 6765 \)
したがって、20番目の値は次のようになります:
\となります。Phi-4は最後まで回答を導くことはできませんでしたが、GPT-4oとo1はどちらも回答を導くことができました。そしてどちらも同じ回答になりました。出力速度としてはGPT-4oの方が速いかなという印象です。
金利計算の精度
次に金利計算を行います。
プロンプトはこちら「A bank has an interest rate of 5% per year, compounded semiannually; find the final amount of 1,000,000 yen deposited for 10 years.」
サンプルコードはこちら
input_text = "A bank has an interest rate of 5% per year, compounded semiannually; find the final amount of 1,000,000 yen deposited for 10 years."
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=250,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: A bank has an interest rate of 5% per year, compounded semiannually; find the final amount of 1,000,000 yen deposited for 10 years. The formula to calculate compound interest is:
\[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]
where \( A \) is the final amount, \( P \) is the principal (initial deposit), \( r \) is the annual interest rate, \( n \) is the number of times the interest is compounded per year, and \( t \) is the time in years.
- [Solution]: To determine the final amount of a deposit with compound interest, we use the formula:
\[ A = P \left(1 + \frac{r}{n}\right)^{nt} \]
Given:
- \( P = 1,000,000 \) yen (the principal)
- \( r = 0.05 \) (annual interest rate of 5%)
- \( n = 2 \) (interest is compounded semiannually)
- \( t = 10 \) years
We can substitute these values into the formula:
\[ A = 1,000結果の日本語訳はこちら
アウトプット ある銀行の金利は年5%、半年複利である。100万円を10年間預金した場合の最終的な金額を求めよ。複利の計算式は
\複利の計算式は次のとおりである。
ここで、[A]は最終的な金額、[P]は元金(最初に預けた金額)、[r]は年利、[n]は年複利の回数、[t]は年数です。
- 解答]: 複利で預金した場合の最終的な金額を求めるには、次式を用いる:
\A=P≦left(1+≦frac{r}{n}}right)^{nt}≦」。
となります:
- 円(元本)。
- r=0.05(年利5%)。
- (利息は半年複利)
- 年
これらの値を式に代入することができる:
\[ A = 1,000こちらは答えが1,000になっていますね。GPT-4oとo1ではどうでしょうか。
GPT-4oの結果はこちら
To calculate the final amount of a deposit with semiannual compounding interest, we use the compound interest formula:
\[A = P \left(1 + \frac{r}{n}\right)^{nt}\]
Where:
- \(A\) is the final amount,
- \(P\) is the principal (initial amount),
- \(r\) is the annual interest rate (as a decimal),
- \(n\) is the number of compounding periods per year,
- \(t\) is the time in years.
### Given:
- \(P = 1,000,000\) yen
- \(r = 5\% = 0.05\)
- \(n = 2\) (compounded semiannually)
- \(t = 10\) years
### Calculation:
Substitute the values into the formula:
\[A = 1,000,000 \left(1 + \frac{0.05}{2}\right)^{2 \cdot 10}\]
Simplify step by step:
1. \(\frac{0.05}{2} = 0.025\),
2. \(2 \cdot 10 = 20\),
3. \((1 + 0.025) = 1.025\),
4. Calculate \(1.025^{20}\).
\[A = 1,000,000 \times (1.025)^{20}\]
Let's compute the exact value for \(A\).
The final amount after 10 years is approximately **1,638,616 yen**.結果の日本語訳はこちら
半年複利の預金の最終金額を計算するには、複利の公式を用いる:
\A = P ⦅left(1 + ⦅frac{r}{n}⦆)^{nt}⦆。
ここで
- (A)は最終金額、
- (P)は元本(当初金額)、
- (r)は年利率(小数)である、
- (n)は年間の複利計算期間数である、
- (t)は年単位の時間である。
### 与えられた:
- P = 1,000,000)円
- \(r = 5\% = 0.05\)
- (n = 2) (半年複利)
- 年
### 計算:
式に代入する:
\A = 1,000,000 ㊟左(1 + ㊟frac{0.05}{2} ㊟右)^{2 ㊟cdot 10
段階的に簡略化する:
1. \(\frac{0.05}{2} = 0.025})、
2. \(2 ˶=20 ˶)、
3. \((1 + 0.025) = 1.025\),
4. (1.025^{20})を計算する。
\A = 1,000,000 ㎟ (1.025)^{20} ㎟。
(A)の正確な値を計算しよう。
10年後の最終的な金額は約1,638,616円**である。o1の結果はこちら
We have an initial principal \( P = 1{,}000{,}000 \) yen, an annual nominal interest rate \( r = 0.05 \) (5%), and the compounding occurs semiannually (twice a year). The total time is \( t = 10 \) years.
**Step-by-step solution:**
1. **Determine the per-period interest rate:**
Since interest is compounded semiannually, there are \( n = 2 \) compounding periods per year.
The interest rate per half-year is:
\[ \frac{r}{n} = \frac{0.05}{2} = 0.025 = 2.5\% \]
2. **Total number of compounding periods:**
Over 10 years, with semiannual compounding, the total number of periods is:
\[ n \times t = 2 \times 10 = 20 \text{ periods} \]
3. **Apply the compound interest formula:**
The future value \( A \) is given by:
\[ A = P \left(1 + \frac{r}{n}\right)^{n \cdot t} \]
Substituting our values:
\[ A = 1{,}000{,}000 \times (1 + 0.025)^{20} \]
\[ A = 1{,}000{,}000 \times (1.025)^{20} \]
4. **Calculating \((1.025)^{20}\):**
Let's approximate \((1.025)^{20}\):
- First, \((1.025)^{10}\):
\((1.025)^{5} \approx 1.1319\) (approximate intermediate calculation)
Then \((1.025)^{10} = (1.1319)^2 \approx 1.2812\)
- Next, \((1.025)^{20} = (1.2812)^{2} \approx 1.6419\)
Thus:
\[ A \approx 1{,}000{,}000 \times 1.6419 = 1{,}641{,}900 \text{ yen} \]
**Final Answer:**
After 10 years, the amount will be approximately:
\[\boxed{1{,}641{,}900 \text{ yen}}\]
Depending on rounding, you might see a figure around 1,642,000 yen, but the above is a close approximation.結果の日本語訳はこちら
元本は当初、1,000,000円、年間の名目金利はr=0.05(5%)とし、複利は半年ごとに(年2回)発生します。合計期間はt=10年です。
**ステップ・バイ・ステップの解答:**
1. **期間ごとの金利を決定する:**
金利は半年ごとに複利計算されるので、1年あたり複利計算期間は\( n = 2\)回ある。
半年ごとの金利は次のとおりである。
\[ r/n = 0.05/2 = 0.025 = 2.5\]
2. **複利計算の期間の合計数:**
10年間、半年ごとに複利計算を行う場合、期間の合計数は:
\[ n × t = 2 × 10 = 20 期間 ]
3. **複利の公式を適用する:**
将来価値(A)は次式で与えられる。
\[ A = P (1 + {r}/{n})^{n・t} ]\]
値を代入する。
\[ A = 1,000,000 × (1 + 0.025) ^{20} ]\]
\[ A = 1{,}000{,}000 × (1.025)^{20} ]
4. **(1.025)^(20]) の計算:**
(1.025)^(20]) を近似してみましょう:
まず、\((1.025)^{10}\):
\((1.025)^{5} ≒ 1.1319\) (概算の中間計算)
次に、\((1.025)^{10} = (1.1319)^2 ≒ 1.2812\)
次に、\((1.025)^(20}) = (1.2812)^(2}) ≒ 1.6419
したがって、
\[ A ≒ 1,000,000 × 1.6419 = 1,641,900 円 ]
**最終的な答え:**
10年後、その金額はおよそ次のようになります。
\[\boxed{1{,}641{,}900円}}\]
四捨五入の仕方によっては、1,642,000円前後の数字になる場合もありますが、上記の数字はそれに近い近似値です。それぞれ回答が割れてしまいました。正直この問題の正解はわからないですね。途中式を見ると近似値を使っているかどうかの違いなような気がします。
ただGPT-4oとo1はそれぞれ近い数字になっているので1,630,000円〜1,642,000円の間に収まるのかなと思います。
幾何学的な推論能力の検証
最後は幾何学的な推論能力の検証です。
プロンプトは「If the volume of a rectangle is 120 cubic centimeters and its height is 6 cm and its width is 4 cm, find its length.」
サンプルコードはこちら
input_text = "If the volume of a rectangle is 120 cubic centimeters and its height is 6 cm and its width is 4 cm, find its length."
inputs = tokenizer(input_text, return_tensors="pt").to("cuda")
with torch.no_grad():
outputs = model.generate(
**inputs,
max_length=250,
do_sample=True,
temperature=0.7,
top_p=0.95,
repetition_penalty=1.1,
pad_token_id=tokenizer.eos_token_id
)
output_text = tokenizer.decode(outputs[0], skip_special_tokens=True)
print("Generated Output:", output_text)結果はこちら
Generated Output: If the volume of a rectangle is 120 cubic centimeters and its height is 6 cm and its width is 4 cm, find its length. <br>
Options:
A. 5 cm<br>
B. 3 cm<br>
C. 7 cm<br>
D. 8 cm<br>
### Response ###
To find the length of the rectangular prism given its volume, height, and width, we can use the formula for the volume of a rectangular prism:
\[\text{Volume} = \text{length} \times \text{width} \times \text{height}\]
We are given:
- Volume \( V = 120 \) cubic centimeters
- Height \( h = 6 \) cm
- Width \( w = 4 \) cm
Let's denote the length by \( l \). Plugging in the known values into the volume formula, we get:
\[120 = l \times 4 \times 6\]
First, simplify the right-hand side:
\[120 = l \times 24\]
Next, solve for \( l \) by dividing both sides of the equation by 24:
\[l = \結果の日本語訳はこちら
生成された出力:長方形の体積が120立方センチメートルで、高さが6センチ、幅が4センチの場合、その長さを求めよ。 <br>
選択肢:
A. 5センチ<br>
B. 3センチ<br>
C. 7センチ<br>
D. 8センチ<br>
### 解答 ###
体積、高さ、幅が与えられた直方体の長さを求めるには、直方体の体積の公式を使用します。
体積 = 長さ × 幅 × 高さ
与えられた値は以下の通りです。
- 体積 V = 120立方センチメートル
- 高さ h = 6センチメートル
- 幅 w = 4センチメートル
長さを l と表記します。体積の公式に既知の値を代入すると、次のようになります。
120 = l × 4 × 6
まず、右辺を簡略化します。
\[120 = l × 24\]
次に、両辺を24で割って、lを求めます。
\[l =\]Phi-4では途中までの式が出ていますが、回答までは導けていないようです。
次にGPT-4oとo1です。
GPT-4oの結果はこちら
To determine the length of the rectangle, given that its volume is \( 120 \, \text{cm}^3 \), height is \( 6 \, \text{cm} \), and width is \( 4 \, \text{cm} \), use the formula for the volume of a rectangular prism:
\[\text{Volume} = \text{Length} \times \text{Width} \times \text{Height}\]
Substitute the known values:
\[120 = \text{Length} \times 4 \times 6\]
Simplify the equation:
\[120 = \text{Length} \times 24\]
Solve for the length:
\[\text{Length} = \frac{120}{24} = 5 \, \text{cm}\]
### Final Answer:
The length of the rectangle is **5 cm**.結果の日本語訳はこちら
\体積]=[長さ]×[幅]×[高さ]の公式を使います。
既知の値を代入する:
\120 = ㎤ 4 ㎤ 6
式を簡略化する:
\120 = ▶テキスト{長さ} ▶倍数24
長さを求めなさい:
\長さ]を求める:[長さ} = ㎤{120}{24} = 5 ㎤, ㎤cm}].
### 最終的な答え
長方形の長さは**5cm**です。o1の結果はこちら
To find the length of the rectangular prism, we use the formula for the volume of a rectangular prism:
\[\text{Volume} = \text{Length} \times \text{Width} \times \text{Height}\]
Given:
- Volume = \( 120 \, \text{cm}^3 \)
- Height = \( 6 \, \text{cm} \)
- Width = \( 4 \, \text{cm} \)
We substitute the known values into the formula:
\[120 = \text{Length} \times 4 \times 6\]
Simplify:
\[120 = \text{Length} \times 24\]
To find the length, divide both sides by 24:
\[\text{Length} = \frac{120}{24}\]
\[\text{Length} = 5 \, \text{cm}\]
### Final Answer:
The length of the rectangle is **5 cm**.結果の日本語訳はこちら
直方体の長さを求めるには、直方体の体積の公式を使います:
\直方体の体積の公式を使います。
与えられた
- 体積 = ㎤( 120 ㎤, ㎤cm}^3 ㎤)
- 高さ = ㎠( 6 ㎠, ㎠text{cm} )
- 幅 = ㎤( 4 ㎤, ㎤cm
既知の値を式に代入します:
\120 = ㎤ 4 ㎤ 6
簡略化する:
\120 = ㎤ 4 ㎤ 6 ㎤ 6
長さを求めるには、両辺を24で割ります:
\両辺を24で割る。
\長さ}=5㎤、長さ}=5㎤、長さ}=5㎤。
### 最終的な答え
長方形の長さは**5cm**です。GPT-4oとo1で回答が一致しました。こちらは正しいように思います。
Phi-4も選択肢として5cmは上がっていましたが、最後まで回答を導き気なかったのが残念です。
max_lengthを増やしても、必ずしも完全な出力が得られるわけではないため、Phi-4の課題でもあるのかなと使っていて感じました。
なお、数学やプログラミング分野で好成績を残しているQwenベースの推論モデルについて詳しく知りたい方は、下記の記事を合わせてご確認ください。

Phi-4についてのよくある質問
まとめ
本記事では、Phi-4のベンチマークや従来のLLMとの比較について紹介しました。
Phi-4とGPT-4o、o1で比較をしてみましたが、生成速度はそこまで変わらず、特にPhi-4はmax_lengthの制限により一部の回答が途中で切れてしまうことがあり、Phi-4の本当の実力が測りきれない場面もありました。
Phi-4は小型ながらに優れたパフォーマンスを発揮するため、今後の活用の幅が広いモデルです。これからPhi-4を使ったWebサービスやアプリケーションが開発されるのが楽しみですね。ぜひ皆さんもPhi-4を活用してみてください!
最後に
いかがだったでしょうか?
Phiを活用した生成AIの導入で、業務効率化や新たなビジネス価値創出を実現しませんか?専門家が御社に最適な活用方法をご提案します。
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、大規模言語モデル(LLM)を対象に、言語理解能力、生成能力、応答速度の各側面について比較・検証した資料も配布しております。この機会にぜひご活用ください。



