Gemini 2.5 Proとは?Googleの思考するAIがついに登場!最新LLMの概要や料金プラン、活用法を徹底解説
- 応答生成前に内部推論を行う思考モデル
- Gemini史上最高の推論・コーディング能力
- マルチモーダル対応&超大容量コンテキスト
2025年3月26日、Googleから新たなLLM「Gemini 2.5 Pro Experimental」がリリースされました!
Gemini 2.5 Pro Experimentalは、これまでで最も知的と位置づけられた次世代モデルであり、回答生成前に内部で「思考」する能力を備えた革新的な大規模言語モデルです。
また、Gemini 2.5 Pro Experimentalの性能は、前モデルのGemini 1.5やGemini 2.0 Proから大幅に進化しており、数学・科学・コードの各種ベンチマークで競合を凌駕する結果を残しているようです。
本記事では、Gemini 2.5 Pro Experimentalの概要や強み、使い方から活用可能性まで網羅的に解説します。
ぜひ最後までご覧ください。
\生成AIを活用して業務プロセスを自動化/
Gemini 2.5 Pro Experimentalの概要
Gemini 2.5 Pro Experimentalは、Google DeepMindチームが開発したGemini 2.5シリーズ最初のモデルであり、「思考モデル (Thinking Model)」と称される新たなカテゴリに属します。
前モデルのGemini 2.0から約3ヶ月でリリースされたことから、Googleの生成AI開発の急速な進展がうかがえますね。
最大の特徴
Gemini 2.5 Pro Experimentalの最大の特徴は「内部で思考するAI」である点です。人間が問題を解く際に、頭の中で論理展開するように、このモデルは応答を生成する前に内部で推論プロセスを踏む仕組みを備えています。
従来の単純なパターンマッチ的回答ではなく、与えられた情報を分析し、文脈やニュアンスを考慮し、論理的結論に至るまで内部で考え抜いてから回答するため、より難解な課題にも対応可能です。いわば「考えてから答えるAI」であり、このコンセプトは、Gemini 2.0のFlash Thinkingモデルで導入された手法をさらに発展させたものとされています。
性能
ミュニティ主導のLLM評価指標である「LMArena(Chatbot Arena)」においては、リリースと同時に総合ランキング1位に躍り出ており、2位以下を大差で引き離す高品質な応答能力を示しています。
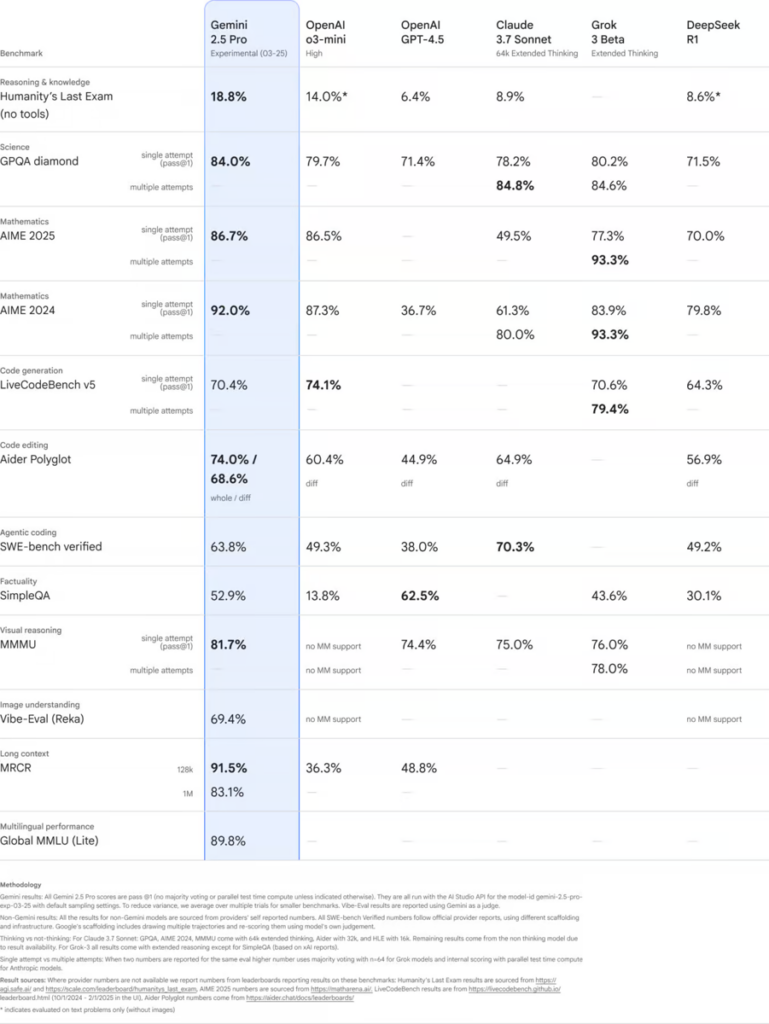
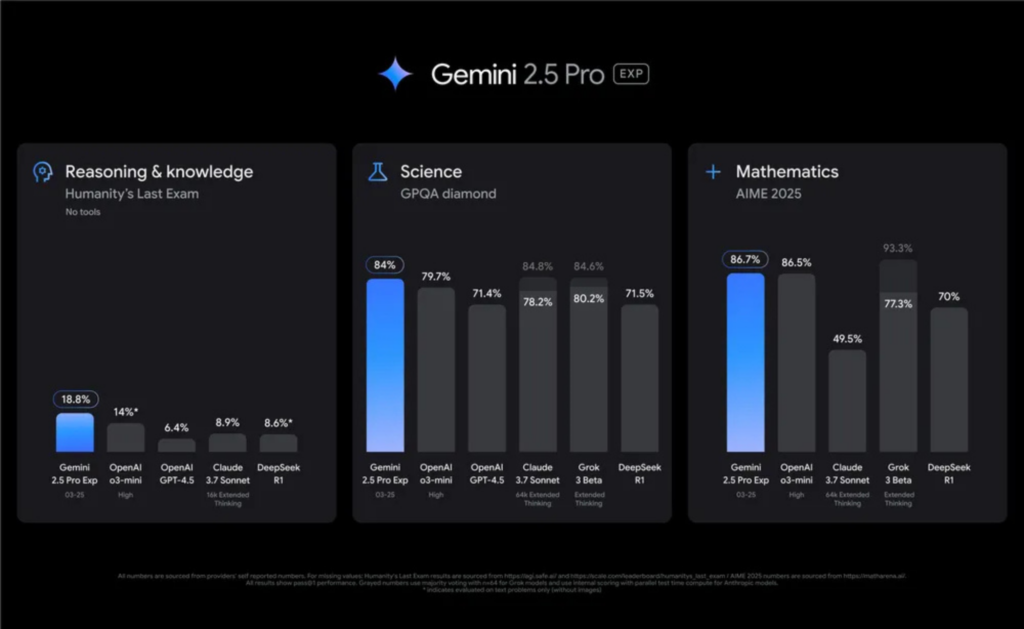
また、Gemini 2.5 Pro Experimentalは、高度な推論能力とコーディング能力を備えています。
「人間の知識と推論の限界」を測る新たなベンチマーク「Humanity’s Last Exam (HLE)」では、18.8%というハイスコアを記録し、OpenAIの競合モデル(o3-miniやGPT-4.5など)を大きく上回っています。
さらに、数学や科学分野の評価指標(GPQAやAIME 2025など)でもトップクラスの成績を収めており、難解な問題解決に強いモデルであることが確認できます。
Gemini 2.5シリーズではこの「考えるAI」というアプローチが基盤となっており、従来のGemini 1.xシリーズでは難しかった推論の飛躍を可能にしてるよう。その結果、人間の専門家に匹敵するような深い分析や判断を要するタスクでも前モデル以上に的確な対応が期待できます。
コーディングスキルを測るAider Polyglotでは68.6%を記録し、OpenAIやAnthropicの最新モデルよりも高いスコアを達成しています。また、ソフトウェア開発全般の指標であるSWE-Bench Verifiedでも、Gemini 2.5 Proは63.8%という結果を残し、OpenAIやDeepSeekの競合モデルを上回っています(ただ、Anthropic Claude 3.7 Sonnetの70.3%には及ばず、ここは今後の課題ともいえます)。
Gemini 2.0 Pro Experimentalとの違い
前モデルGemini 2.0 Pro Experimentalとの違いはどこにあるのでしょうか?以下の表にまとめます。
| Gemini 2.0 Pro Experimental | Gemini 2.5 Pro Experimental | |
|---|---|---|
| リリース状況 | 2025年2月〜 一般開放 | 試験プレビュー版 |
| マルチモーダル入力 | ⭕️ | ⭕️ |
| テキスト出力 | ⭕️ | ⭕️ |
| 画像出力 | ❌️(今後追加予定) | ❌️(今後追加予定) |
| 音声出力 | ❌️(今後追加予定) | ❌️(今後追加予定) |
| マルチモーダルLive API | ❌️(今後追加予定) | ❌️(今後追加予定) |
| コンテキストウィンドウ | 200万トークン | 100万トークン(将来的に200万トークンに拡張予定) |
| 構造化出力 | ⭕️ | ⭕️ |
| 検索ツールの利用 | ⭕️ | ⭕️ |
| コード実行ツールの利用 | ⭕️ | ⭕️ |
| 推論能力 | 高い | 非常に高い |
| コーディング能力 | 非常に高い | 最先端(コード生成性能が大幅向上) |
| モデルサイズ | 非公開(外部報告では約5,400億パラメータ規模と推測されている) | 非公開(推定 数百億〜数千億規模以上) |
推論やコーディング能力が向上しているのが見てわかりますね・・!
Gemini 2.5 Pro Experimentalの料金プラン
2025年3月26日時点で、Gemini 2.5 Pro Experimentalを利用するには、有料サブスクリプション「Gemini Advanced」への加入が必要でした。
現在は、Google AI StudioやGeminiアプリ、Vertex AIなど複数のプラットフォームから利用可能となっています。既存のGemini Advancedプラン加入者は、ダッシュボード上でモデルを切り替えるだけで自動的に最新バージョン「Gemini 2.5 Pro Preview(05-06)」へ移行でき、追加の設定は不要です。
Gemini Advancedは、Googleの提供する生成AIサービスのプレミアムプランで、個人向けには月額19.99ドルで提供されています。
日本円では、為替レートにもよりますが月額約2,500円前後です。なお、初月無料キャンペーンが適用される場合もあります。このプランに加入すると、従来のGemini標準モデルに加えて最先端モデルであるGemini 2.5 Proシリーズへのアクセス権が付与されるようになります。
また、Google AI Studioでは一定の無料枠が用意されており、小規模な利用や試用も可能。利用料金は従量課金制もあり、API利用の際は処理したトークン数に応じて課金されます。
Gemini 2.5 Pro Experimentalのライセンス
Gemini 2.5 Pro Experimentalは「実験提供」という位置づけのモデルであるため、利用にはいくつか制約や条件があります。以下、主なライセンスを表形式でまとめます。
| 利用用途 | 可否 | 備考 |
|---|---|---|
| 商用利用 | ⭕️ | 一定の制限がある場合あり |
| 改変 | 🔺 | 基本NGだが、API経由の二次的著作物の生成はOKの場合あり |
| 配布 | 🔺 | ソフトウェア自体の配布はNGだが、生成されたコンテンツはOKの場合あり |
| 私的利用 | ⭕️ | |
| 特許利用 | ❌ | 特許権やその他知的財産権はGoogle側に帰属 |
Gemini 2.5 Pro Experimentalモデルそのものはクローズドソースであり、ユーザーがその内部構造を閲覧・取得することはできません。また、リバースエンジニアリングやモデルのエクスポートを試みることも禁止されています。
一方で、モデルが生成した出力コンテンツの権利については、Googleはユーザーが生成した内容の所有権を主張しないと明言されています。つまり、ユーザーが、Gemini 2.5 Proを使って作成したテキストやコードなどの成果物は基本的にユーザーに帰属し、自由に利用できます
ただ、医療や法務など専門分野での利用にも制限があります。例えば、医療診断や治療助言への利用(医療機器規制の対象となるような用途)は禁止されています。
利用する際には、最新のライセンス情報を確認するようにしましょう。
Gemini 2.5 Pro Experimentalの使い方
実際に、Gemini 2.5 Pro Experimentalを使ってみましょう。
Gemini Advancedプラン契約済みの方向けになりますが、基本的な利用手順と解説します。
Gemini Advancedに加入・ログインする
以前は、Gemini 2.5 Pro Experimentalを使うには、前述のGemini Advancedプランへの加入が必要でした。現在は、Google AI StudioやGeminiアプリ、Vertex AIからも利用できるようになっています。
既存ユーザーは、ダッシュボード上でモデルを切り替えるだけで自動的に最新バージョン(05-06)へ移行でき、追加の設定は不要です。
Google AI Studioの場合、Googleアカウントでサインインし、Model欄から「Gemini 2.5 Pro Preview 05-06」を選ぶだけで利用開始できます。
Geminiアプリでも、モデル選択画面から「2.5 Pro(Preview 05-06)」を選ぶと、すぐに新しい機能を体験できます。
Vertex AI経由でも同じモデルを呼び出せるので、開発用途にも幅広く対応しています。
Gemini 2.5 Pro Experimental使ってみた
Gemini 2.5 Pro Experimentalのコーディング性能と数学問題解決性能の高さを確認したいため、今回は、前モデルGemini 2.0 Pro Experimental(Flash Thinking)と比較しながら、タスクを解いてもらいます。
コーディングタスク
入力プロンプトこちら
あなたは優秀なソフトウェアエンジニアです。
以下の要件に従って、「巡回セールスマン問題(Traveling Salesman Problem, TSP)」を効率的に近似解法するPythonコードをゼロから作成してください。
問題設定:
ある営業担当者が複数の都市を1回ずつすべて訪問し、最終的に元の都市に戻る最短ルートを探します(都市間距離は自由に定義可能)。
都市数は10個以上を想定(具体例として15都市でテスト)。
各都市間の距離データはランダムに生成(乱数シードで再現可能に)。
要求するアルゴリズム:
遺伝的アルゴリズム(Genetic Algorithm, GA)を用いて実装。
貪欲法(Greedyアルゴリズム)による初期解生成を組み合わせて精度を高める。
世代数・個体数・突然変異率などのパラメータを明示し、柔軟に変更可能にすること。
コードに含めて欲しいポイント:
クラスや関数を利用した読みやすい構造
コメントによるロジックの分かりやすい説明
都市間の経路と最終的なルートの長さを表示する機能
matplotlibなどを使い、最終的なルートを視覚化(オプション)
提出時の注意:
外部ライブラリはnumpyとmatplotlibのみ利用可
コードは完全に実行可能であることGemini 2.0 Pro Experimentalの結果はこちら
import numpy as np
import random
import matplotlib.pyplot as plt
class TSP:
"""
巡回セールスマン問題(TSP)を遺伝的アルゴリズムで解くクラス
"""
def __init__(self, num_cities, random_seed=None, population_size=100, generations=500, mutation_rate=0.01):
"""
初期化
Args:
num_cities (int): 都市の数
random_seed (int, optional): 乱数シード. Defaults to None.
population_size (int, optional): 個体数. Defaults to 100.
generations (int, optional): 世代数. Defaults to 500.
mutation_rate (float, optional): 突然変異率. Defaults to 0.01.
"""
self.num_cities = num_cities
self.random_seed = random_seed
if random_seed is not None:
np.random.seed(random_seed)
random.seed(random_seed)
self.population_size = population_size
self.generations = generations
self.mutation_rate = mutation_rate
self.distances = self._generate_distances()
self.population = self._generate_initial_population()
self.best_route = None
self.best_distance = float('inf')
self.history =
def _generate_distances(self):
"""
都市間の距離行列をランダムに生成
Returns:
numpy.ndarray: 都市間の距離行列 (num_cities x num_cities)
"""
distances = np.zeros((self.num_cities, self.num_cities))
for i in range(self.num_cities):
for j in range(i + 1, self.num_cities):
distances[i, j] = random.randint(10, 100) # 10から100の間のランダムな距離
distances[j, i] = distances[i, j]
return distances
def _calculate_distance(self, route):
"""
与えられた経路の総距離を計算
Args:
route (list): 都市の順序を示すリスト
Returns:
int: 経路の総距離
"""
total_distance = 0
for i in range(self.num_cities):
current_city = route[i]
next_city = route[(i + 1) % self.num_cities] # 最後の都市から最初の都市への距離も考慮
total_distance += self.distances[current_city, next_city]
return total_distance
def _greedy_initial_solution(self):
"""
貪欲法を用いて初期解を生成
Returns:
list: 貪欲法で得られた経路
"""
start_city = random.randint(0, self.num_cities - 1)
unvisited_cities = list(range(self.num_cities))
unvisited_cities.remove(start_city)
current_city = start_city
route = [start_city]
while unvisited_cities:
nearest_city = -1
min_distance = float('inf')
for city in unvisited_cities:
distance = self.distances[current_city, city]
if distance < min_distance:
min_distance = distance
nearest_city = city
route.append(nearest_city)
unvisited_cities.remove(nearest_city)
current_city = nearest_city
return route
def _generate_initial_population(self):
"""
初期集団を生成(一部は貪欲法による解を含む)
Returns:
list: 初期集団(経路のリスト)
"""
initial_population =
# 貪欲法による初期解を1つ加える
greedy_solution = self._greedy_initial_solution()
initial_population.append(greedy_solution)
# 残りの個体はランダムな順序で生成
for _ in range(self.population_size - 1):
route = list(range(self.num_cities))
random.shuffle(route)
initial_population.append(route)
return initial_population
def _evaluate_population(self):
"""
集団内の各個体の適応度(総距離)を評価
Returns:
list: (距離, 経路) のタプルのリスト。距離が短いほど適応度が高い
"""
evaluated_population =
for route in self.population:
distance = self._calculate_distance(route)
evaluated_population.append((distance, route))
if distance < self.best_distance:
self.best_distance = distance
self.best_route = route
evaluated_population.sort(key=lambda x: x[0]) # 距離でソート
return evaluated_population
def _select_parents(self, evaluated_population):
"""
ルーレット選択で親個体を選択
Args:
evaluated_population (list): 評価済みの個体群
Returns:
list: 選択された親個体のペアのリスト
"""
total_fitness = sum(1 / distance for distance, _ in evaluated_population) # 距離の逆数を適応度とする
if total_fitness == 0:
# 全ての個体の距離が無限大の場合の処理(通常は起こらないはず)
return random.sample(evaluated_population, 2)
parents =
for _ in range(self.population_size // 2): # 次世代の個体数の半分だけ親を選択
# ルーレット選択
parent1 = self._roulette_wheel_selection(evaluated_population, total_fitness)
parent2 = self._roulette_wheel_selection(evaluated_population, total_fitness)
parents.append((parent1[1], parent2[1])) # 経路のみを保存
return parents
def _roulette_wheel_selection(self, evaluated_population, total_fitness):
"""
ルーレット選択の補助関数
"""
pick = random.uniform(0, total_fitness)
current_sum = 0
for distance, route in evaluated_population:
current_sum += 1 / distance
if current_sum > pick:
return (distance, route)
return evaluated_population[-1] # 誤差対策
def _crossover(self, parent1, parent2):
"""
順序交叉(Ordered Crossover)
Args:
parent1 (list): 親個体1の経路
parent2 (list): 親個体2の経路
Returns:
tuple: 2つの子個体の経路
"""
start = random.randint(0, self.num_cities - 2)
end = random.randint(start + 1, self.num_cities - 1)
child1 = [-1] * self.num_cities
child2 = [-1] * self.num_cities
# 親1の部分配列をそのまま子1にコピー
for i in range(start, end + 1):
child1[i] = parent1[i]
# 親2から子1にまだ含まれていない都市を順に追加
index = end + 1
for city in parent2:
if city not in child1:
if index >= self.num_cities:
index = 0
child1[index] = city
index += 1
# 親2の部分配列をそのまま子2にコピー
for i in range(start, end + 1):
child2[i] = parent2[i]
# 親1から子2にまだ含まれていない都市を順に追加
index = end + 1
for city in parent1:
if city not in child2:
if index >= self.num_cities:
index = 0
child2[index] = city
index += 1
return child1, child2
def _mutate(self, route):
"""
突然変異(隣接都市の入れ替え)
Args:
route (list): 突然変異させる経路
Returns:
list: 突然変異後の経路
"""
if random.random() < self.mutation_rate:
index1 = random.randint(0, self.num_cities - 1)
index2 = (index1 + 1) % self.num_cities
route[index1], route[index2] = route[index2], route[index1]
return route
def run_ga(self):
"""
遺伝的アルゴリズムを実行
"""
for generation in range(self.generations):
evaluated_population = self._evaluate_population()
self.history.append(self.best_distance)
if generation % 50 == 0:
print(f"世代: {generation}, 最良距離: {self.best_distance}")
parents = self._select_parents(evaluated_population)
next_generation =
# エリート戦略:現在の最良個体を次世代に残す
next_generation.append(evaluated_population[0][1])
for parent1, parent2 in parents:
child1, child2 = self._crossover(parent1, parent2)
next_generation.append(self._mutate(child1))
next_generation.append(self._mutate(child2))
# 次世代の個体数が設定されたサイズを超えないように調整
self.population = next_generation[:self.population_size]
print("\n最終結果:")
print(f"最良経路: {self.best_route}")
print(f"最良距離: {self.best_distance}")
def display_result(self):
"""
最終的なルートの情報を表示
"""
if self.best_route:
print("\n都市間の経路:")
for i in range(self.num_cities):
current_city = self.best_route[i]
next_city = self.best_route[(i + 1) % self.num_cities]
print(f"{current_city} -> {next_city} (距離: {self.distances[current_city, next_city]})")
print(f"\n最終的なルートの総距離: {self.best_distance}")
else:
print("GAが実行されていません。")
def visualize_route(self):
"""
最終的なルートをmatplotlibで可視化(オプション)
"""
if not self.best_route:
print("GAが実行されていません。")
return
# ランダムに都市の座標を生成(可視化用)
np.random.seed(self.random_seed) # 距離生成と同じシードを使用
city_coords = np.random.rand(self.num_cities, 2) * 100
plt.figure(figsize=(10, 10))
# 都市のプロット
plt.scatter(city_coords[:, 0], city_coords[:, 1], c='red', marker='o', s=100)
for i, coord in enumerate(city_coords):
plt.annotate(str(i), xy=coord, xytext=(5, 5), textcoords='offset points')
# ルートのプロット
for i in range(self.num_cities):
current_city_index = self.best_route[i]
next_city_index = self.best_route[(i + 1) % self.num_cities]
plt.plot([city_coords[current_city_index, 0], city_coords[next_city_index, 0]],
[city_coords[current_city_index, 1], city_coords[next_city_index, 1]],
'blue', linewidth=1)
plt.title(f"TSP 最良ルート (距離: {self.best_distance:.2f})")
plt.xlabel("X座標")
plt.ylabel("Y座標")
plt.grid(True)
plt.show()
# 世代ごとの最良距離の推移をプロット
plt.figure(figsize=(10, 6))
plt.plot(self.history)
plt.title("世代ごとの最良距離の推移")
plt.xlabel("世代")
plt.ylabel("最良距離")
plt.grid(True)
plt.show()
if __name__ == "__main__":
num_cities = 15
random_seed = 42
population_size = 150
generations = 1000
mutation_rate = 0.02
tsp_solver = TSP(num_cities=num_cities,
random_seed=random_seed,
population_size=population_size,
generations=generations,
mutation_rate=mutation_rate)
tsp_solver.run_ga()
tsp_solver.display_result()
tsp_solver.visualize_route()Gemini 2.5 Pro Experimentalの結果はこちら
import numpy as np
import random
import matplotlib.pyplot as plt
import math
class TSP_GA:
"""
遺伝的アルゴリズムを用いて巡回セールスマン問題(TSP)を解くクラス。
貪欲法による初期解生成を組み込む。
"""
def __init__(self, num_cities, population_size, generations, mutation_rate, tournament_size, seed=None):
"""
初期化メソッド
Args:
num_cities (int): 都市の数
population_size (int): 集団内の個体数 (偶数を推奨)
generations (int): GAを実行する世代数
mutation_rate (float): 突然変異率 (0.0 ~ 1.0)
tournament_size (int): トーナメント選択で使用する個体数
seed (int, optional): 乱数シード. Defaults to None.
"""
if population_size % 2 != 0:
print("警告: 個体数は偶数にすることを推奨します。")
self.num_cities = num_cities
self.population_size = population_size
self.generations = generations
self.mutation_rate = mutation_rate
self.tournament_size = tournament_size
self.seed = seed
if self.seed is not None:
random.seed(self.seed)
np.random.seed(self.seed)
# 都市の座標をランダムに生成 (0から100の範囲)
self.cities_coordinates = np.random.rand(self.num_cities, 2) * 100
# 都市間の距離行列を計算
self.distance_matrix = self._calculate_distance_matrix()
# 集団を初期化
self.population = self._initialize_population()
self.best_solution = None
self.best_distance = float('inf')
self.history = [] # 各世代の最良距離を記録
def _calculate_distance(self, city1_coord, city2_coord):
"""2都市間のユークリッド距離を計算"""
return np.linalg.norm(city1_coord - city2_coord)
def _calculate_distance_matrix(self):
"""都市間の距離行列を計算"""
matrix = np.zeros((self.num_cities, self.num_cities))
for i in range(self.num_cities):
for j in range(i + 1, self.num_cities):
dist = self._calculate_distance(self.cities_coordinates[i], self.cities_coordinates[j])
matrix[i, j] = dist
matrix[j, i] = dist
return matrix
def _calculate_route_distance(self, route):
"""指定された経路(route)の総距離を計算"""
total_distance = 0
for i in range(self.num_cities):
from_city = route[i]
# 最後の都市からは最初の都市へ戻る
to_city = route[(i + 1) % self.num_cities]
total_distance += self.distance_matrix[from_city, to_city]
return total_distance
def _greedy_initial_solution(self, start_node=0):
"""貪欲法による初期解(経路)を生成"""
current_node = start_node
unvisited = list(range(self.num_cities))
unvisited.remove(current_node)
route = [current_node]
while unvisited:
nearest_neighbor = min(unvisited, key=lambda city: self.distance_matrix[current_node, city])
route.append(nearest_neighbor)
unvisited.remove(nearest_neighbor)
current_node = nearest_neighbor
return np.array(route)
def _initialize_population(self):
"""集団を初期化。1つは貪欲解、残りはランダムな経路"""
population = []
# 1. 貪欲法による解を追加
greedy_route = self._greedy_initial_solution()
population.append(greedy_route)
# 2. 残りの個体をランダムな順列で生成
base_route = list(range(self.num_cities))
for _ in range(self.population_size - 1):
# 単純なランダムシャッフル
shuffled_route = random.sample(base_route, len(base_route))
# もしくは貪欲解を少し変更するなど、他の初期化方法も考えられる
# 例:一部をランダムに入れ替える
# modified_greedy = greedy_route.copy()
# idx1, idx2 = random.sample(range(self.num_cities), 2)
# modified_greedy[idx1], modified_greedy[idx2] = modified_greedy[idx2], modified_greedy[idx1]
# population.append(modified_greedy)
population.append(np.array(shuffled_route))
return population
def _tournament_selection(self):
"""トーナメント選択により親個体を1つ選択"""
tournament_candidates_indices = random.sample(range(self.population_size), self.tournament_size)
tournament_candidates = [self.population[i] for i in tournament_candidates_indices]
# 距離が最も短い個体(最も適応度が高い)を選択
winner = min(tournament_candidates, key=self._calculate_route_distance)
return winner
def _order_crossover(self, parent1, parent2):
"""順序交叉(Order Crossover, OX1)を実行"""
size = len(parent1)
child = [-1] * size # 子個体を初期化
# 交叉する部分配列の開始・終了インデックスをランダムに選択
start, end = sorted(random.sample(range(size), 2))
# parent1の部分配列をchildにコピー
child[start:end+1] = parent1[start:end+1]
# parent2の要素をchildの残りの位置に、順序を保ちつつ挿入
parent2_idx = 0
child_idx = 0
while -1 in child: # childが完全に埋まるまで
if child_idx == start: # コピー済みの部分に来たらスキップ
child_idx = end + 1
if child_idx >= size: # スキップ後、範囲外になったら先頭から再開
child_idx = 0
if start == 0: # startが0の場合、end+1以降しか空きがない
continue # このループの残りはスキップして次のparent2要素へ
# parent2の現在の要素がchildにまだ含まれていないかチェック
current_parent2_city = parent2[parent2_idx % size]
if current_parent2_city not in child:
# childの現在の空き位置(-1)に挿入
if child[child_idx % size] == -1:
child[child_idx % size] = current_parent2_city
child_idx += 1 # childの次の位置へ
else:
# 稀なケースだが念のため:child_idxが埋まっている場合は次に進める
# (通常、上記のif child_idx == start: で処理されるはず)
child_idx += 1
parent2_idx += 1 # parent2の次の要素へ
# デバッグ用: childに-1が残っていないか、重複がないか確認
if -1 in child:
print("エラー: 交叉後に未割り当ての都市があります。")
print("Parent1:", parent1)
print("Parent2:", parent2)
print("Start, End:", start, end)
print("Child:", child)
# ここでエラー処理やデバッグ情報の出力を追加できます
# とりあえず、一時的に親のどちらかを返すなど
return parent1 # エラー時はparent1を返す(要検討)
if len(set(child)) != size:
print("エラー: 交叉後に重複または欠落した都市があります。")
print("Parent1:", parent1)
print("Parent2:", parent2)
print("Start, End:", start, end)
print("Child:", child)
return parent1 # エラー時はparent1を返す(要検討)
return np.array(child)
def _swap_mutation(self, route):
"""突然変異(Swap Mutation): ルート内の2都市をランダムに入れ替える"""
mutated_route = route.copy()
if random.random() < self.mutation_rate:
# 入れ替える2つのインデックスをランダムに選択
idx1, idx2 = random.sample(range(self.num_cities), 2)
mutated_route[idx1], mutated_route[idx2] = mutated_route[idx2], mutated_route[idx1]
return mutated_route
def run(self):
"""遺伝的アルゴリズムを実行"""
print(f"遺伝的アルゴリズムを開始します...")
print(f"パラメータ: 都市数={self.num_cities}, 個体数={self.population_size}, 世代数={self.generations}, 突然変異率={self.mutation_rate}, トーナメントサイズ={self.tournament_size}, 乱数シード={self.seed}")
# 初期集団の最良解を評価
initial_distances = [self._calculate_route_distance(route) for route in self.population]
current_best_idx = np.argmin(initial_distances)
self.best_distance = initial_distances[current_best_idx]
self.best_solution = self.population[current_best_idx]
self.history.append(self.best_distance)
print(f"初期集団の最良距離 (貪欲法含む): {self.best_distance:.4f}")
for generation in range(self.generations):
new_population = []
# 1. エリート主義: 現世代の最良個体を次世代にそのまま残す
# 厳密には現時点での全体ベストを残す方が良い場合もあるが、
# ここではシンプルに現世代のベストを1つ残す
current_distances = [self._calculate_route_distance(route) for route in self.population]
elite_idx = np.argmin(current_distances)
elite = self.population[elite_idx]
new_population.append(elite)
# 2. 新しい個体を生成 (交叉と突然変異)
while len(new_population) < self.population_size:
# 親を選択
parent1 = self._tournament_selection()
parent2 = self._tournament_selection()
# 同じ親が選ばれた場合は再選択(任意)
# while np.array_equal(parent1, parent2):
# parent2 = self._tournament_selection()
# 交叉
child1 = self._order_crossover(parent1, parent2)
# 交叉がペアで子を生成する場合 (例: OX2) は2つ作る
# child2 = self._order_crossover(parent2, parent1) # 必要なら
# 突然変異
mutated_child1 = self._swap_mutation(child1)
# mutated_child2 = self._swap_mutation(child2) # 必要なら
new_population.append(mutated_child1)
# new_population.append(mutated_child2) # ペアで生成する場合
# 個体数が奇数になる場合を考慮し、ループ条件で調整
if len(new_population) >= self.population_size:
break # 個体数に達したらループ終了
# 集団を更新
self.population = new_population[:self.population_size] # サイズ超過分を切り捨て
# 現世代の最良解を評価し、全体での最良解を更新
current_distances = [self._calculate_route_distance(route) for route in self.population]
current_best_idx = np.argmin(current_distances)
current_best_distance = current_distances[current_best_idx]
if current_best_distance < self.best_distance:
self.best_distance = current_best_distance
self.best_solution = self.population[current_best_idx]
self.history.append(self.best_distance) # 各世代の最良距離を記録
# 進捗表示 (例: 10世代ごと)
if (generation + 1) % 10 == 0 or generation == self.generations - 1:
print(f"世代 {generation + 1}/{self.generations} - 現在の最良距離: {self.best_distance:.4f}")
print("遺伝的アルゴリズムが完了しました。")
return self.best_solution, self.best_distance
def get_best_solution(self):
"""最終的に見つかった最良解とその距離を返す"""
if self.best_solution is None:
print("エラー: run() メソッドを実行して解を見つけてください。")
return None, float('inf')
return self.best_solution, self.best_distance
def plot_route(self, route, title="TSP Route"):
"""指定された経路をmatplotlibで描画"""
if route is None:
print("描画する経路がありません。")
return
plt.figure(figsize=(10, 8))
# 都市の座標をプロット
plt.scatter(self.cities_coordinates[:, 0], self.cities_coordinates[:, 1], c='red', s=100, label='Cities')
# 都市の番号を表示
for i, (x, y) in enumerate(self.cities_coordinates):
plt.text(x, y + 1, str(i), ha='center', va='bottom') # y+1 で少し上に表示
# 経路を線で結ぶ
route_coords = self.cities_coordinates[route]
# 最後の都市から最初の都市へ戻る線も描画
route_coords_closed = np.vstack([route_coords, route_coords[0]])
plt.plot(route_coords_closed[:, 0], route_coords_closed[:, 1], 'b-', label='Route')
# 開始都市を強調表示(任意)
start_city_coord = self.cities_coordinates[route[0]]
plt.scatter(start_city_coord[0], start_city_coord[1], c='green', s=150, marker='*', label='Start City')
plt.title(title)
plt.xlabel("X Coordinate")
plt.ylabel("Y Coordinate")
plt.legend()
plt.grid(True)
plt.axis('equal') # X軸とY軸のスケールを合わせる
plt.show()
def plot_history(self):
"""学習過程(各世代の最良距離)をプロット"""
if not self.history:
print("学習履歴がありません。")
return
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(self.history) + 1), self.history, marker='o', linestyle='-')
plt.title('Best Distance per Generation')
plt.xlabel('Generation')
plt.ylabel('Total Distance')
plt.grid(True)
plt.show()
# --- パラメータ設定 ---
NUM_CITIES = 15 # 都市数
POPULATION_SIZE = 50 # 集団内の個体数
GENERATIONS = 200 # GAの世代数
MUTATION_RATE = 0.1 # 突然変異率 (例: 10%)
TOURNAMENT_SIZE = 5 # トーナメント選択のサイズ
RANDOM_SEED = 42 # 乱数シード (再現性のため)
# --- GAの実行 ---
tsp_solver = TSP_GA(
num_cities=NUM_CITIES,
population_size=POPULATION_SIZE,
generations=GENERATIONS,
mutation_rate=MUTATION_RATE,
tournament_size=TOURNAMENT_SIZE,
seed=RANDOM_SEED
)
best_route, best_distance = tsp_solver.run()
# --- 結果の表示 ---
print("\n--- 結果 ---")
if best_route is not None:
print(f"最終的に見つかった最短経路: {best_route}")
print(f"最短経路長: {best_distance:.4f}")
# 最適経路の描画
tsp_solver.plot_route(best_route, title=f"Best TSP Route Found (Distance: {best_distance:.4f})")
# 学習履歴の描画
tsp_solver.plot_history()
else:
print("解が見つかりませんでした。")
# 参考:貪欲法のみの結果
greedy_route = tsp_solver._greedy_initial_solution()
greedy_distance = tsp_solver._calculate_route_distance(greedy_route)
print(f"\n参考: 貪欲法のみの経路: {greedy_route}")
print(f"参考: 貪欲法のみの経路長: {greedy_distance:.4f}")
# tsp_solver.plot_route(greedy_route, title=f"Greedy Algorithm Route (Distance: {greedy_distance:.4f})")どちらも素晴らしい出力結果ですが、「可読性」、「パラメータ調整の容易さ」、「拡張性やメンテナンス性」の観点でGemini 2.5 Pro Experimentalの生成結果が優れているように感じます。
数学&コーディングタスク
入力プロンプトこちら
あなたは数値解析と数論の専門家です。
以下の要件に従って、数論分野における重要な未解決問題である「Goldbach予想(ゴールドバッハの予想)」を近似的に数値検証するアルゴリズムをPythonでゼロから実装してください。
問題設定:
「Goldbach予想」とは『4以上の偶数はすべて、2つの素数の和で表すことができる』という未解決の仮説です。
今回は、非常に大きな偶数(例えば10億〜20億程度)を範囲として、この予想が本当に成り立つかを近似的に検証するアルゴリズムを設計・実装します。
要求されるアルゴリズム:
入力として「下限」と「上限」を指定(例えば下限=1,000,000,000、上限=1,000,000,500)。
指定された範囲内のすべての偶数について、2つの素数の和で表現可能かどうかを近似的に検証する効率的な方法を設計。
検証には「確率的素数判定法(Miller-Rabin法など)」を用いて効率化を図る。
コードに含めるべきポイント:
計算アルゴリズムの設計思想や採用した手法について、詳細なコメントを記述。
アルゴリズムの精度と速度を調整できるようにパラメータ(素数判定の繰り返し回数など)を導入。
検証結果を分かりやすくレポート(例えば『検証した偶数の数、検証に成功した偶数、予想に反した偶数(もしあれば)』を明示的に表示)。
評価の基準:
数論に関する理解度や知識の深さ。
提案した数値検証アルゴリズムの効率性(実行時間)と精度。
コードの読みやすさ(アルゴリズム設計思想や各処理の目的がコメントから明確に理解可能か)。
提出時の注意:
利用可能な外部ライブラリは標準ライブラリとNumPyのみ。
実行可能であることを前提に、完成したコードを提示。Gemini 2.0 Pro Experimentalの結果はこちら
import random
import math
import time
import numpy as np # 要求には含まれているが、今回の実装では標準ライブラリのみを使用します
class GoldbachVerifier:
"""
ゴールドバッハ予想を近似的に数値検証するためのクラス。
指定された範囲内のすべての偶数について、2つの素数の和で表現可能かどうかを、
確率的素数判定法(Miller-Rabin法)を用いて効率的に検証します。
"""
def __init__(self, miller_rabin_iterations=20):
"""
コンストラクタ。
Args:
miller_rabin_iterations (int): Miller-Rabin法の繰り返し回数。
この値を大きくすると素数判定の精度は向上しますが、
実行時間も増加します。デフォルトは20です。
"""
self.miller_rabin_iterations = miller_rabin_iterations
def power(self, base, exp, modulus):
"""
モジュラ指数演算を行います。base^exp mod modulus を効率的に計算します。
バイナリ法(繰り返し二乗法)を使用しています。
Args:
base (int): 底。
exp (int): 指数。
modulus (int): 法。
Returns:
int: base^exp mod modulus の結果。
"""
res = 1
base %= modulus
while exp > 0:
if exp % 2 == 1:
res = (res * base) % modulus
exp >>= 1
base = (base * base) % modulus
return res
def is_prime_miller_rabin(self, n):
"""
Miller-Rabin法を用いて、与えられた数が素数であるかどうかを確率的に判定します。
Args:
n (int): 判定する整数。
Returns:
bool: True (nは素数である可能性が高い), False (nは合成数である可能性が高い)。
"""
# いくつかの既知の小さい素数に対する特別なケース
if n <= 1:
return False
if n <= 3:
return True
if n % 2 == 0:
return False
# n-1 = 2^s * d の形式に分解 (dは奇数)
s = 0
d = n - 1
while d % 2 == 0:
s += 1
d //= 2
# 繰り返しテストを実行
for _ in range(self.miller_rabin_iterations):
# ランダムな基数 a を選択 (1 < a < n-1)
a = random.randrange(2, n - 1)
x = self.power(a, d, n)
if x == 1 or x == n - 1:
continue
# s-1 回の繰り返し
for _ in range(s - 1):
x = self.power(x, 2, n)
if x == n - 1:
break
else:
# 上記のループが break しなかった場合、n は合成数である可能性が高い
return False
# 全てのテストを通過した場合、n は素数である可能性が高い
return True
def verify_goldbach(self, lower_bound, upper_bound):
"""
指定された範囲内のすべての偶数について、ゴールドバッハ予想を近似的に検証します。
Args:
lower_bound (int): 検証する偶数の下限(4以上)。
upper_bound (int): 検証する偶数の上限。
Returns:
tuple: 検証結果の統計情報を含むタプル
(検証した偶数の数, 検証に成功した偶数の数, 予想に反した偶数(もしあれば)のリスト)。
"""
if lower_bound < 4 or lower_bound % 2 != 0:
print("警告: 下限は4以上の偶数である必要があります。")
lower_bound = max(4, lower_bound + (lower_bound % 2))
verified_count = 0
success_count = 0
failed_count =
start_time = time.time()
for n in range(lower_bound, upper_bound + 1, 2):
verified_count += 1
found_pair = False
# 2から n/2 までの範囲で素数 p1 を探索
for p1 in range(2, n // 2 + 1):
if self.is_prime_miller_rabin(p1):
p2 = n - p1
if self.is_prime_miller_rabin(p2):
success_count += 1
found_pair = True
break # 1つの素数ペアが見つかれば十分
if not found_pair:
failed_count.append(n)
print(f"警告: {n} は2つの素数の和で表現できませんでした (Miller-Rabin法による判定)。")
end_time = time.time()
elapsed_time = end_time - start_time
print("\n検証結果:")
print(f"検証した偶数の数: {verified_count}")
print(f"検証に成功した偶数の数: {success_count}")
if failed_count:
print(f"予想に反した偶数(Miller-Rabin法による判定): {failed_count}")
else:
print("指定された範囲内のすべての偶数について、2つの素数の和で表現できる可能性が高いです (Miller-Rabin法による判定)。")
print(f"検証に要した時間: {elapsed_time:.2f} 秒")
return verified_count, success_count, failed_count
# メインの実行部分
if __name__ == "__main__":
lower_bound = 1_000_000_000
upper_bound = 1_000_000_500
verifier = GoldbachVerifier(miller_rabin_iterations=10) # 繰り返し回数を調整して精度と速度を調整
print(f"ゴールドバッハ予想の数値検証を開始します (範囲: {lower_bound} ~ {upper_bound})")
verifier.verify_goldbach(lower_bound, upper_bound)
print("検証が完了しました。")Gemini 2.5 Pro Experimentalの結果はこちら
import random
import time
import sys
# ==============================================================================
# Miller-Rabin確率的素数判定法の実装
# ==============================================================================
def is_prime(n, k=40):
"""
Miller-Rabin確率的素数判定法を用いて、数値nが素数かどうかを判定する。
Args:
n (int): 判定対象の整数。
k (int): 判定の繰り返し回数(精度パラメータ)。回数が多いほど精度は高まるが、計算時間が増加する。
デフォルトは40回で、実用上十分な精度が得られる。
Returns:
bool: nが確率的に素数であればTrue、合成数であればFalse。
設計思想:
- 大きな数に対して決定論的な素数判定(例:試し割り法)は非常に時間がかかるため、高速な確率的素数判定法であるMiller-Rabin法を採用。
- Fermatの小定理 (a^(n-1) ≡ 1 (mod n)) に基づくが、カーマイケル数のような反例が存在するため、より強力な判定法を用いる。
- n - 1 = 2^s * d (dは奇数) と分解し、ランダムに選んだ基数aに対して、a^d mod n == 1 または a^(2^r * d) mod n == n-1 (0 <= r < s) が成り立つかをk回テストする。
- いずれのテストでも成り立たない場合、nは合成数であると判定できる。
- k回のテストをすべてパスした場合、nは高い確率で素数であると判定する(ただし、100%ではない)。
"""
# 基本ケースの処理
if n < 2:
return False
if n == 2 or n == 3:
return True
if n % 2 == 0:
return False
# n - 1 = 2^s * d となる s, d を見つける (dは奇数)
d = n - 1
s = 0
while d % 2 == 0:
d //= 2
s += 1
# k回の繰り返しテスト
for _ in range(k):
a = random.randrange(2, n - 1) # 1 < a < n-1 の範囲でランダムな基数aを選ぶ
x = pow(a, d, n) # x = a^d mod n を計算
# a^d ≡ 1 (mod n) または a^d ≡ -1 (mod n) の場合
if x == 1 or x == n - 1:
continue # 次の繰り返しへ
# r を 1 から s-1 まで変化させてチェック
composite = True
for _ in range(s - 1):
x = pow(x, 2, n) # x = x^2 mod n
if x == n - 1:
composite = False # -1 (mod n) になれば確率的素数の可能性がある
break
if x == 1: # 1 になってしまったら合成数(非自明な平方根が見つかった)
return False
# ループを抜けても -1 (mod n) にならなかった場合、合成数
if composite:
return False
# k回のテストをすべてパスした場合、確率的に素数であると判定
return True
# ==============================================================================
# Goldbach予想の数値検証アルゴリズム
# ==============================================================================
def verify_goldbach(lower_bound, upper_bound, k=40):
"""
指定された範囲内の偶数について、Goldbach予想が成り立つかを近似的に検証する。
Args:
lower_bound (int): 検証範囲の下限(含む)。
upper_bound (int): 検証範囲の上限(含む)。
k (int): is_prime関数に渡すMiller-Rabin法の繰り返し回数。
設計思想:
- Goldbach予想は「4以上の全ての偶数は、2つの素数の和で表せる」というもの。
- 指定された範囲 [lower_bound, upper_bound] 内の偶数nを順に調べる。
- 各偶数nに対して、n = p + q となる素数p, qのペアを探す。
- 効率化のため、探索する素数pは 3 から n/2 までとする。
- もし p > n/2 なら、q = n - p < n/2 となり、pが小さい方の探索でカバーされるため。
- p=2の場合も考慮する (n = 2 + (n-2))。
- 素数判定には、上で実装したis_prime関数(Miller-Rabin法)を用いる。これにより、巨大な数の素数判定を高速に行う。
- 確率的素数判定法を用いているため、この検証は「近似的」なものとなる。Miller-Rabin法が合成数を誤って素数と判定する(偽陽性)可能性は非常に低いが存在する。
- 検証結果(チェックした偶数の数、成功数、失敗数)を集計し、レポートする。
"""
print(f"検証範囲: {lower_bound:,} から {upper_bound:,}")
print(f"Miller-Rabin法の繰り返し回数 k = {k}")
print("検証を開始します...")
total_even_checked = 0
succeeded_count = 0
failed_numbers = [] # 予想に反した(と思われる)偶数を格納するリスト
# 開始時刻を記録
start_time = time.time()
# 偶数nについてループ (lower_bound以上、upper_bound以下)
# 開始が奇数の場合、次の偶数から始める
current_n = lower_bound if lower_bound % 2 == 0 else lower_bound + 1
# 4未満の偶数は対象外
if current_n < 4:
current_n = 4
processed_count = 0
report_interval = max(1, (upper_bound - lower_bound + 1) // 1000) # 進捗表示の間隔調整
while current_n <= upper_bound:
total_even_checked += 1
processed_count += 1
# --- 進捗表示 ---
if processed_count % report_interval == 0:
elapsed_time = time.time() - start_time
progress = (current_n - lower_bound) / (upper_bound - lower_bound + 1) * 100
sys.stdout.write(f"\r進捗: {progress:.2f}% ({current_n:,} / {upper_bound:,}) 経過時間: {elapsed_time:.2f}秒")
sys.stdout.flush()
# ---------------
found_pair = False
# 1. p=2 の場合をチェック
q = current_n - 2
if is_prime(q, k):
# print(f"{current_n} = 2 + {q}") # デバッグ用
found_pair = True
# 2. pが3以上の奇数の場合をチェック
if not found_pair:
# pは 3 から n/2 まで奇数のみチェック
for p in range(3, current_n // 2 + 1, 2):
# まずpが素数かチェック
if is_prime(p, k):
q = current_n - p
# qが素数かチェック (qもp>=3より奇数になる)
if is_prime(q, k):
# print(f"{current_n} = {p} + {q}") # デバッグ用
found_pair = True
break # ペアが見つかったらこの偶数nのチェックは終了
# ペアが見つかったかどうかに基づいてカウント
if found_pair:
succeeded_count += 1
else:
# Miller-Rabin法が失敗した可能性もあるが、ここでは「予想に反した」候補とする
failed_numbers.append(current_n)
current_n += 2 # 次の偶数へ
# 最終的な進捗表示を完了させる
elapsed_time = time.time() - start_time
sys.stdout.write(f"\r進捗: 100.00% ({upper_bound:,} / {upper_bound:,}) 経過時間: {elapsed_time:.2f}秒\n")
sys.stdout.flush()
# 検証結果のレポート
print("\n" + "="*30)
print("検証結果レポート")
print("="*30)
print(f"検証した偶数の総数: {total_even_checked:,}")
print(f"Goldbach予想を満たした偶数の数: {succeeded_count:,}")
failed_count = len(failed_numbers)
print(f"Goldbach予想を満たさない可能性のある偶数の数: {failed_count:,}")
if failed_count > 0:
print("該当する偶数:")
# 多数ある場合は一部のみ表示
if failed_count <= 20:
print(failed_numbers)
else:
print(f"{failed_numbers[:10]} ... (他 {failed_count-10} 件)")
print("="*30)
print(f"検証に要した時間: {elapsed_time:.2f} 秒")
print("="*30)
if failed_count > 0:
print("\n注意:")
print("Miller-Rabin法は確率的素数判定法であるため、素数でない数を素数と誤判定する(偽陽性)可能性がゼロではありません。")
print("「予想を満たさない可能性のある偶数」がリストされた場合、それは必ずしもGoldbach予想の反例ではありません。")
print("より高い精度(kの値を増やす)で再検証するか、決定論的な素数判定法での確認が必要です。")
# ==============================================================================
# メイン実行ブロック
# ==============================================================================
if __name__ == "__main__":
# --- パラメータ設定 ---
# 検証範囲 (例: 10億から10億500まで)
LOWER_BOUND = 1_000_000_000
UPPER_BOUND = 1_000_000_500
# LOWER_BOUND = 4
# UPPER_BOUND = 1000
# Miller-Rabin法の繰り返し回数 (精度)
# 値を大きくすると精度が上がるが、計算時間が増加する。40程度で実用上十分。
MILLER_RABIN_ITERATIONS = 40
# --- 検証の実行 ---
print("=" * 50)
print("Goldbach予想 近似数値検証プログラム")
print("=" * 50)
verify_goldbach(LOWER_BOUND, UPPER_BOUND, MILLER_RABIN_ITERATIONS)
print("\n検証プログラムを終了します。")先ほどのコーディングタスクと比べて、より一層、「コードの可読性」が上がっていることがお分かりいただけると思います。
Gemini 2.5 Pro Experimentalは、コメントが充実しており、変数名、関数名が明確でロジックもわかりやすく実装されています。
難解なタスクもお手の物といったところでしょうか。
Gemini 2.5 Pro Experimentalの活用可能性
高性能な大規模言語モデル「Gemini 2.5 Pro Experimental」が今後どのように活用され得るか、その応用可能性について考察していきます。
現時点でも、既に高い性能を持つGemini 2.5 Pro Experimentalですが、正式版リリースやさらなるアップデートに伴い、様々な領域でAI活用の在り方を塗り替えていくことが期待されます。
ビジネス分野
前述のように、メール対応や資料作成補助などオフィス業務での効率化は大きなテーマです。Gemini 2.5 Proの登場により、ルーチン業務の完全自動化が一層現実味を帯びてきました。
単純な繰り返し業務はAIエージェントに任せ、人間はより創造的なタスクに専念する流れが加速していくと考えられます。また、専門知識が必要な作業でもAIがリアルタイムアシストすることで、生産性向上が見込まれます。例えば、膨大なデータ分析や報告書作成も、AIが下準備を整え、人間が結果を判断するというハイブリッド体制が一般化すると考えられます。
Google社も今後Geminiを定期的にアップデートし、クラウドサービスや業務ツールとのさらなる統合を推し進めていくと発表しています。将来的には、「AIに任せる」から「AIと協働する」時代へシフトしていき、Geminiはその中核を担う存在になっていくでしょう。
教育・学習分野
膨大な知識を持ち、推論力に優れるGemini 2.5 Pro Experimentalは、高度な家庭教師や学習支援AIとしての可能性も秘めています。
例えば、学生が難解な数学問題に取り組む際、解き方のヒントを段階的に与えたり、誤答に対して「どこで論理が食い違ったか」フィードバックするといった対話型チュータリングが期待できます。
従来の教育用AIは、浅いQAに留まりがちでしたが、思考プロセスを持つモデルならではの深い解説や異なる視点の提示ができると考えられます。
さらに、100万トークンのコンテキストを活かし、教科書や参考文献を丸ごと読み込ませて質疑応答させるなど、大規模知識ベースを用いた学習も可能です。
教育現場での活用には慎重さも必要ですが、個別最適化学習を支えるAIパートナーとして、将来、クラスに一人Geminiがいるような状況も想像できますね。
クリエイティブ・開発分野
Gemini 2.5 Pro Experimentalの創造的応用としては、「コンテンツ制作」や「ソフトウェア開発」が挙げられます。
既に、テキストやコード生成の高い能力は実証されていますが、これをさらに発展させて、企画段階からプロトタイプ構築までAIが補助する流れが一般化するかもしれません。
例えば、ゲーム業界では、「こんなゲームを作りたい」というアイデアを入力すると、Geminiが簡易なプロトタイプコードやストーリーラインを提案してくれるようになるかもしれません。
同様に映像制作でも、脚本のドラフトやシーンの描写をAIが作成し、人間がブラッシュアップするといった協働が進みそうです。
Gemini 2.5 Pro Experimentalは画像生成自体は行いませんが、他の画像生成AIと連携するマルチモーダル創作も視野に入ってきますね。
gemini-2.5-pro-preview-05-06公開プレビュー版リリース情報
2025年5月6日に「gemini-2.5-pro-preview-05-06」がリリースされました。ダッシュボード上の切り替え操作を行うだけで前バージョンから自動で移行でき、追加設定は不要です。プレビュー版利用者向けに専用フォーラムも用意されており、安定性や動作に関する意見を投稿できます。
これらのポイントを押さえた上で、最後にアップデートされた新しい機能について詳しく見ていきましょう。
コーディング支援機能のアップグレード
HTMLの構造をしっかり読み取ってくれるようになったおかげで、モックアップをそのまま再現するのが楽になりました。JavaScriptでは、よくある変数ミスを自動で検出し修正候補を出してくれます。その分、手直しの手間が少なく済み、ビルドエラーの発生も大幅に減りました。
ウェブアプリ構築サポートの進化
「WebDev Arena」で旧バージョンに大差をつけたのは、新しいレイアウト解析の仕組みのおかげです。ドラッグ&ドロップで作ったデザインをそのまま渡すと、必要なクラス名やスタイル設定が返ってきます。処理は軽く、短い待ち時間で済むので、自分でコーディングする時間を削減できます。
画内容の理解能力強化
動画の字幕やカットポイントをピンポイントで判別できるようになりました。そのため、学習アプリを組むときに章立てやクイズ作成がスムーズです。公開サンプルでは、YouTube動画を渡すだけで見出しリストを自動生成し、スライド資料にまとめる機能が試せます。
開発者向けの使い勝手改善
大量にリクエストを投げても、自動的に負荷を分散してエラーを防いでくれます。問題が起こったときはステータスに応じた間隔で再試行してくれるので、スクリプトが止まる心配がありません。
APIキーは環境変数で管理できる仕組みも備わっており、セキュリティ面の安心感が高まりました。
利用環境と価格情報
利用するにはGoogle AI Studioのアカウントが必要ですが、無料枠が引き続き用意されています。Vertex AIからも同じモデルを呼び出せるので、プロジェクト間で設定を使い回せます。
料金はリクエスト数と処理時間に応じた従量課金制で、旧バージョンと変わりません。最新の請求レポートでコストの動きをチェックしやすくなっています。
Gemini 2.5 Proに関するFAQ
Gemini 2.5 Pro導入を検討している方や使い方に迷っている方に向けて、よくある質問とその答えをまとめました。気になるポイントを確認しながら、ぜひ参考にしてください。
Gemini 2.5 Proを使ってみよう
Gemini 2.5 Pro Experimentalの登場は、生成AIの新たなステージの幕開けです。2025年5月6日には、さらに進化した「Gemini 2.5 Pro Preview(05-06)」がリリースされ、コーディング支援やウェブアプリ構築、動画理解などの新機能が追加されました。
その思考力によってAIがこなせる仕事の幅は着実に広がっています。
ビジネスでは効率化と競争力強化、教育では個別最適な学習支援、開発・創作では発想からアウトプットまでのプロセス革新と、様々な分野で波及効果が見込まれます。
Googleは、今後もモデルの改良と使い勝手の向上を進めるとみられ、私たちユーザーもその進化に合わせてAIとの協働方法をアップデートしていく必要があると思います。
Gemini 2.5 Pro Experimentalは、AIが人間のパートナーとして、ますます知的に振る舞う未来への大きな一歩であり、今後の展開から目が離せません!

最後に
いかがだったでしょうか?
生成AIは、単なる業務の自動化だけでなく、クリエイティブな業務支援や開発の効率化、社内DXの推進など、企業の多くの領域で活用できます。
貴社の事業にどう活かせるか、具体的な導入事例や最適な活用方法をご提案できますので、ぜひご相談ください。
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、大規模言語モデル(LLM)を対象に、言語理解能力、生成能力、応答速度の各側面について比較・検証した資料も配布しております。この機会にぜひご活用ください。





