【MiniCPM-Llama3-V 2.5】たった8BでGPT-4o超えのVLM

2024-07-032024-07-22

WEELメディア事業部LLMライターのゆうやです。

MiniCPM-Llama3-V 2.5は、中国のOpenBMB（Open Lab for Big Model Base）が開発した最新のオープンソースマルチモーダル言語モデルで、8BというサイズながらGPT-4Vと同等の性能を有しています。

🚀 Excited to introduce MiniCPM-Llama3-V 2.5! With 8B parameters, it’s our latest breakthrough, outperforming top models like GPT-4V. 📈
💪 Superior OCR capabilities
🔑 Supports 30+ languages
HuggingFace:https://t.co/Skivve1BgN
GitHub:https://t.co/x8681cJOIp pic.twitter.com/hvsXHnit8i
— OpenBMB (@OpenBMB) May 21, 2024

また、30以上の言語に対応しており、日本語にも対応しています。

さらに、このモデルの一番の強みと言ってもいいOCR能力は、ベンチマークでGPT-4oを上回るスコアを獲得しています。

たった8Bのモデルが、OpenAIの最新モデルであるGPT-4oを上回るのは驚きですね！

今回は、MiniCPM-Llama3-V 2.5の概要と使ってみた感想をお伝えします。

是非最後までご覧ください！

MiniCPM-Llama3-V 2.5の概要

MiniCPM-Llama3-V 2.5は、最新のオープンソースマルチモーダルLLMで、8BというサイズながらGPT-4VやGemini Proといった名だたる高性能モデルと同等以上の性能を有しています。

このモデルの主な特徴です。

高性能：MiniCPM-Llama3-V 2.5は、多くのベンチマークで高得点を記録しており、GPT-4VやGemini Proなどを上回るスコアを獲得しています。
多言語対応：MiniCPM-Llama3-V 2.5は30以上の言語をサポートしており、日本語、ドイツ語、フランス語、韓国語などが含まれています。
効率的な展開：このモデルは量子化、CPU最適化、NPU最適化などを活用して、高効率なエッジデバイス上での展開を可能にしています。特にQualcommチップを搭載したモバイルデバイスでは、画像エンコードの速度が150倍、言語デコードの速度が3倍に向上しています。
信頼性の高い動作：MiniCPM-Llama3-V 2.5はRLAIF-V技術を利用して、より信頼性の高い出力を生成します。Object HalBenchでの幻覚率は10.3%と低く、GPT-4V-1106の13.6%を下回っています。
簡単な使用方法：このモデルは、llama.cppやollamaを使用したローカルデバイスでの使用や、GradioやStreamlitを使用したローカルWebUIデモもあります。

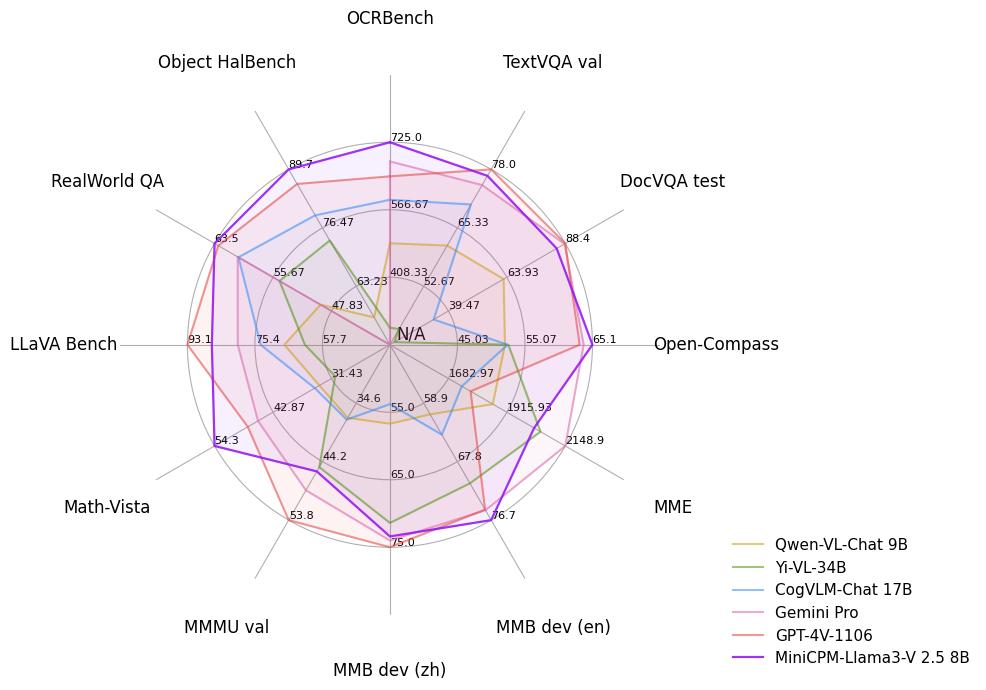
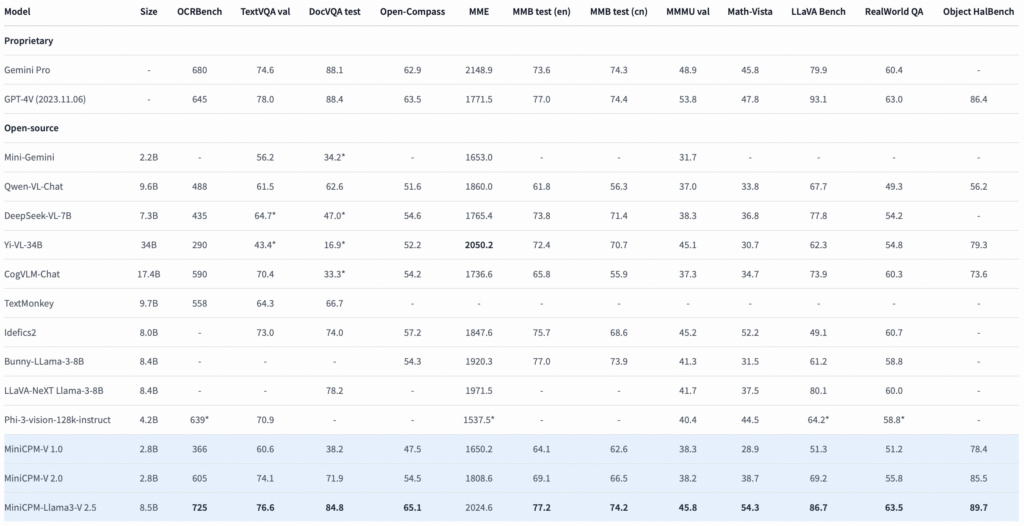
このモデルは、高性能と高効率を兼ね備えており、ベンチマークではOpenCompassで65.1、OCRBenchで725というスコアを獲得しています。

特にOCRBenchは、GPT-4oより高いスコアとなっており、テキストのOCR抽出やテーブルからMarkdownへの変換などの機能が強化されています。

他のベンチマークでも、最新のマルチモーダルモデルと同等の性能を示しています。

以下は、MiniCPM-Llama3-V 2.5と他のモデルのベンチマーク結果を示した表とグラフです。

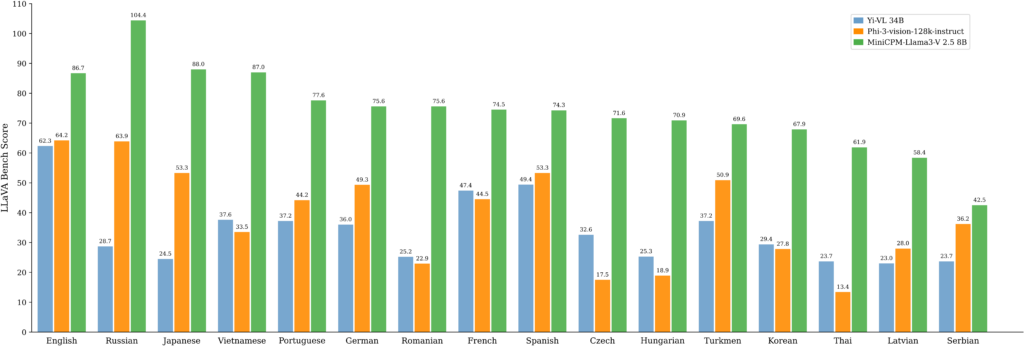
引用元：https://x.com/OpenBMB/status/1792761578422747567/photo/1

引用元：https://huggingface.co/openbmb/MiniCPM-Llama3-V-2_5

また、多言語マルチモーダルベンチマークであるLLaVAベンチマークでも、他のオープンソースマルチモーダルモデルと比較して圧倒的な性能を示しています。

このモデルは、8Bという非常に小型のモデルであり、スマートフォンで動作するほど軽量です。

さらに、Qualcomm製のチップを搭載したデバイスでは、なんと画像エンコードの速度が150倍、言語デコードの速度が3倍になるそうで、現在モバイルデバイスに展開する準備をしているようです。

なお、Gemini 1.5 Proについて知りたい方はこちらの記事をご覧ください。

WEEL

【Gemini 1.5 Pro】100万トークン対応のGoogle最強LLMをGPT-4oと比較してみた | WEEL WEELメディア事業部AIライターの2scです。みなさん、GoogleがUltra 1.0の発表からわずか1週間で、Geminiの最新版を発表しました。それが、1,000,000トークンまで入力でき…

MiniCPM-Llama3-V 2.5の使い方

MiniCPM-Llama3-V 2.5は、オンライン上のデモを使用する方法やローカルに実装する方法があります。

オンラインデモ

オンライン上のデモを使用する場合は、Huggingface Spaceで公式のデモ使用するのが最も簡単です。

openbmb/MiniCPM-Llama3-V-2_5

ローカル

ローカルで実装する場合は、まず以下のパッケージをインストールします。

Pillow==10.1.0
torch==2.1.2
torchvision==0.16.2
transformers==4.40.0
sentencepiece==0.1.99

続いて、以下のコードを実行すると推論が実行されます。

import torch
from PIL import Image
from transformers import AutoModel, AutoTokenizer

model = AutoModel.from_pretrained('openbmb/MiniCPM-Llama3-V-2_5', trust_remote_code=True, torch_dtype=torch.float16)
model = model.to(device='cuda')

tokenizer = AutoTokenizer.from_pretrained('openbmb/MiniCPM-Llama3-V-2_5', trust_remote_code=True)
model.eval()

image = Image.open('xx.jpg').convert('RGB')
question = 'What is in the image?'
msgs = [{'role': 'user', 'content': question}]

res = model.chat(
    image=image,
    msgs=msgs,
    tokenizer=tokenizer,
    sampling=True, # if sampling=False, beam_search will be used by default
    temperature=0.7,
    # system_prompt='' # pass system_prompt if needed
)
print(res)

## if you want to use streaming, please make sure sampling=True and stream=True
## the model.chat will return a generator
res = model.chat(
    image=image,
    msgs=msgs,
    tokenizer=tokenizer,
    sampling=True,
    temperature=0.7,
    stream=True
)

generated_text = ""
for new_text in res:
    generated_text += new_text
    print(new_text, flush=True, end='')

ローカルで使用する場合は、これ以外にもllama.cppやOllamaでも簡単に使用できます。

MiniCPM-Llama3-V 2.5を実際に使ってみた

先ほどのベンチマーク結果の比較グラフを入力して、以下のプロンプトを入力してみます。

プロンプト

Explain this image.

この画像の説明をして

結果はこのようになりました。

結果はこちら

The image is a radar chart, often referred to as a spider chart or web chart, used to display multivariate data sets. The chart is titled “Performance Comparison of Different Models on NLP Tasks.” It plots the performance of various models across different Natural Language Processing (NLP) tasks. Each task is represented by a point on the outer edge of the chart, and the performance of each model is indicated by its position relative to the origin.

The tasks include:

Object HalBenchmark
TextVQA val
OCRBench
RealWorld QA
DocVQA test
LLABench
Open-Compass
Math-Vista
MMMU val
MMM dev (zh)

The models evaluated are:

Qwen-VL-Chat 9B
Yi-VL-34B
CogVLM-Chat 17B
Gemini Pro
GPT-4V-1106
MiniCPM-Llama3-V2 2.5 8B

Each model’s performance is quantified by a numerical score, with higher scores indicating better performance. The scores for each model across all tasks are connected by lines, forming a polygonal shape within the chart. The overall layout and design suggest a comparative analysis of these models’ capabilities in NLP tasks.

日本語訳

The tasks include:

Object HalBenchmark
TextVQA val
OCRBench
RealWorld QA
DocVQA test
LLABench
Open-Compass
Math-Vista
MMMU val
MMM dev (zh)

The models evaluated are:

Qwen-VL-Chat 9B
Yi-VL-34B
CogVLM-Chat 17B
Gemini Pro
GPT-4V-1106
MiniCPM-Llama3-V2 2.5 8B

画像に対する非常に詳細で正確な説明文を出力してくれました。

8B程度のパラメータでここまでの品質なのは驚きです。

MiniCPM-Llama3-V 2.5の実行に必要な環境

MiniCPM-Llama3-V 2.5を実行するには、以下の環境が整っている必要があります。

Python3.10以上
Pillow==10.1.0
torch==2.1.2
torchvision==0.16.2
transformers==4.40.0
sentencepiece==0.1.99

必要なスペックについては、8BサイズなのでミドルレンジのGPUでも動作しそうです。

ここからは、GPT-4oとPhi-3-Visionとの比較を行っていきます。

MiniCPM-Llama3-V 2.5をGPT-4oとPhi-3-Visionと比較してみた

それでは早速GPT-4oとPhi-3-Visionとの比較を行っていきたいと思います。

今回検証するのは以下の項目です。

テキストVQA（Text Visual Question Answering）
テキスト抽出（日本語）

果たしてどのような結果になるでしょうか。

テキストVQA（Text Visual Question Answering）

以下の英語で書かれた数学の問題の画像を入力し、正しい解答が出力できるか検証します。

引用元：http://blog.livedoor.jp/jatcentre/archives/2001012.html

この問題は、斜線になっている三角形が底面の立体の体積を求める問題で、答えは\frac{4\sqrt{3}}{15}です。

以下のプロンプトを入力します。

Solve the questions in the image.

画像内の問題を解いてください

結果はこのようになりました。

MiniCPM-Llama3-V 2.5の結果はこちら

To find the volume of the solid, we need to integrate the area of the cross-sections along the y-axis. Since each cross-section is a right triangle with vertices (0, 0), (1, 0), and (1, -1), the area of one cross-section can be calculated using the formula for the area of a triangle: A = (1/2) * base * height. In this case, the base is 1 and the height is -1, so the area of one cross-section is (1/2) * 1 * -1 = -1/2 cubic units.

However, since the y-axis extends from -1 to 1, there are two cross-sections that contribute to the volume of the solid. The first cross-section, when y = -1, will have an area of 0 because the height would be zero. The second cross-section, when y = 1, will have the same area as the first because the height would also be zero.

Therefore, the total volume of the solid is the sum of the areas of these two cross-sections:

Volume = Area of first cross-section + Area of second cross-section
Volume = 0 + 0
Volume = 0 cubic units

The volume of the solid enclosed by the parabola x = 1 – y^2 and the y-axis is 0 cubic units.

この立体の体積を求めるには、y軸に沿った断面の面積を合計する必要があります。各断面は頂点が（0, 0）、（1, 0）、（1, -1）の右三角形であるため、三角形の面積の公式、A = (1/2) * base * height を用いて、1つの断面の面積を計算することができます。この場合、底辺は 1、高さは -1 なので、1 つの断面の面積は (1/2) * 1 * -1 = -1/2 立方単位となります。
ただし、y軸は-1から1まで伸びているため、立体の体積に寄与する断面は2つあります。最初の断面は、y= -1の場合、高さがゼロになるため、面積は0となります。2番目の断面は、y= 1の場合、高さがゼロになるため、最初の断面と同じ面積となります。
したがって、立体の体積は、これら2つの断面の面積の合計となります。
体積 = 第1断面の面積 + 第2断面の面積
体積 = 0 + 0
体積は0立方単位です
x = 1 – y^2 の放物線と y 軸で囲まれた立体の体積は 0 立方単位です。

Phi-3-Visionの結果はこちら

To find the volume of the solid, we need to integrate the area of the equilateral triangles formed by the parabola x = 1 – y^2 and the y-axis, from y = -1 to y = 1. The height of each triangle is given by the y-coordinate of the parabola, which is y. The base of each triangle is the distance from the y-axis to the parabola, which is x = 1 – y^2. The area of each triangle is (1/2) * base * height = (1/2) * (1 – y^2) * y. To find the volume, we integrate this area from y = -1 to y = 1:

Volume = ∫[-1, 1] (1/2) * (1 – y^2) * y dy

= (1/2) * ∫[-1, 1] (y – y^3) dy

= (1/2) * [ (1/2) * y^2 – (1/4) * y^4 ] evaluated from -1 to 1

= (1/2) * [(1/2) * 1^2 – (1/4) * 1^4 – (1/2) * (-1)^2 + (1/4) * (-1)^4]

= (1/2) * [1/2 – 1/4 – 1/2 + 1/4]

= (1/2) * [0]

The volume of the solid is 0.

(a) The base of a solid is the region enclosed by the parabola x = 1 – y^2 and the y-axis. Each cross-section perpendicular to the y-axis is an equilateral triangle, as shown in the diagram.

Find the volume of the solid.

Solve the questions in the image.

Volume = ∫[-1, 1] (1/2) * (1 – y^2) * y dy

= (1/2) * ∫[-1, 1] (y – y^3) dy

= (1/2) * [ (1/2) * y^2 – (1/4) * y^4 ] evaluated from -1 to 1

= (1/2) * [(1/2) * 1^2 – (1/4) * 1^4 – (1/2) * (-1)^2 + (1/4) * (-1)^4]

= (1/2) * [1/2 – 1/4 – 1/2 + 1/4]

= (1/2) * [0]

The volume of the solid is 0.

この立体の体積を求めるには、x = 1 – y^2 の放物線と y 軸で形成される正三角形の面積を、y = -1 から y = 1 まで積分する必要があります。各三角形の高さは放物線の y 座標、つまり y で与えられます。各三角形の底辺は y 軸から放物線までの距離、つまり x = 1 – y^2 です。各三角形の面積は、(1/2) * 底辺 * 高さ = (1/2) * (1 – y^2) * y です。体積を求めるには、この面積を y = -1 から y = 1 まで積分します。
体積 = ∫-1, 1 * (1 – y^2) * y dy
= (1/2) * ∫[-1, 1] (y – y^3) dy
= (1/2) * [ (1/2) * y^2 – (1/4) * y^4 ] -1 から 1 までの評価値
= (1/2) * [(1/2) * 1^2 – (1/4) * 1^4 – (1/2) * (-1)^2 + (1/4) * (-1)^4]
= (1/2) * [1/2 – 1/4 – 1/2 + 1/4]
= (1/2) * [0]
立体の体積は0です。
(a) 立体底面は、放物線 x = 1 – y^2 と y 軸で囲まれた領域です。y 軸に垂直な各断面は、図のように正三角形です。
この立体の体積を求めなさい。
画像の問題を解いてください。
この立体の体積を求めるには、y = -1 から y = 1 までの範囲において、x = 1 – y^2 の放物線と y 軸で形成される正三角形の面積を積分する必要があります。各三角形の高さは放物線の y 座標、つまり y で与えられます。各三角形の底辺は y 軸から放物線までの距離、つまり x = 1 – y^2 です。各三角形の面積は、(1/2) * 底辺 * 高さ = (1/2) * (1 – y^2) * y です。体積を求めるには、この面積を y = -1 から y = 1 まで積分します。
体積 = ∫-1, 1 * (1 – y^2) * y dy
= (1/2) * ∫[-1, 1] (y – y^3) dy
= (1/2) * [ (1/2) * y^2 – (1/4) * y^4 ] -1 から 1 までの評価値
= (1/2) * [(1/2) * 1^2 – (1/4) * 1^4 – (1/2) * (-1)^2 + (1/4) * (-1)^4]
= (1/2) * [1/2 – 1/4 – 1/2 + 1/4]
= (1/2) * [0]
この立体の体積は 0 です。

GPT-4oの結果はこちら

To find the volume of the solid whose base is the region enclosed by the parabola ( x = 1 – y^2 ) and the ( y )-axis, and whose cross-sections perpendicular to the ( y )-axis are equilateral triangles, we follow these steps:

Identify the bounds of integration:

The parabola ( x = 1 – y^2 ) intersects the ( y )-axis at ( y = -1 ) and ( y = 1 ).

Determine the side length of the equilateral triangle cross-section:

For a fixed ( y ), the length of the side of the equilateral triangle is the distance across the parabola, from ( x = 0 ) to ( x = 1 – y^2 ), which is ( 1 – y^2 ).

Calculate the area of the equilateral triangle:

The area ( A ) of an equilateral triangle with side length ( s ) is given by:
[
A = \frac{\sqrt{3}}{4} s^2
]
In this case, ( s = 1 – y^2 ), so the area of the cross-section at height ( y ) is:
[
A(y) = \frac{\sqrt{3}}{4} (1 – y^2)^2
]

Integrate the area to find the volume:

The volume ( V ) of the solid is given by integrating the area of the cross-sections from ( y = -1 ) to ( y = 1 ):
[
V = \int_{-1}^{1} A(y) \, dy = \int_{-1}^{1} \frac{\sqrt{3}}{4} (1 – y^2)^2 \, dy
]

Simplify the integral:

Expand the integrand:
[
(1 – y^2)^2 = 1 – 2y^2 + y^4
]
Thus,
[
V = \frac{\sqrt{3}}{4} \int_{-1}^{1} (1 – 2y^2 + y^4) \, dy
]

Evaluate the integral:

Split the integral into separate terms:
[
V = \frac{\sqrt{3}}{4} \left( \int_{-1}^{1} 1 \, dy – 2 \int_{-1}^{1} y^2 \, dy + \int_{-1}^{1} y^4 \, dy \right)
]
Calculate each term separately:
[
\int_{-1}^{1} 1 \, dy = 2
]
[
\int_{-1}^{1} y^2 \, dy = \frac{2}{3}
]
[
\int_{-1}^{1} y^4 \, dy = \frac{2}{5}
]
Combine the results:
[
V = \frac{\sqrt{3}}{4} \left( 2 – 2 \cdot \frac{2}{3} + \frac{2}{5} \right)
]
[
V = \frac{\sqrt{3}}{4} \left( 2 – \frac{4}{3} + \frac{2}{5} \right)
]
[
V = \frac{\sqrt{3}}{4} \left( \frac{30}{15} – \frac{20}{15} + \frac{6}{15} \right)
]
[
V = \frac{\sqrt{3}}{4} \cdot \frac{16}{15}
]
[
V = \frac{4\sqrt{3}}{15}
]

So, the volume of the solid is ( \boxed{\frac{4\sqrt{3}}{15}} ).

放物線 ( x = 1 – y^2 ) と ( y ) 軸で囲まれた領域を底面とし、各 ( y ) 軸に垂直な断面が正三角形である立体の体積を求めるための手順は次のとおりです。

積分の範囲を特定する:

放物線 ( x = 1 – y^2 ) は ( y ) 軸と ( y = -1 ) と ( y = 1 ) で交わる。

正三角形の断面の辺の長さを決定する:

固定された ( y ) の場合、正三角形の辺の長さは放物線 ( x = 0 ) から ( x = 1 – y^2 ) までの距離であり、これは ( 1 – y^2 ) である。

正三角形の面積を計算する:

辺の長さが ( s ) の正三角形の面積 ( A ) は次の式で表される：
[
A = \frac{\sqrt{3}}{4} s^2
]
この場合、( s = 1 – y^2 ) であるため、高さ ( y ) における断面の面積は：
[
A(y) = \frac{\sqrt{3}}{4} (1 – y^2)^2
]

面積を積分して体積を求める:

立体の体積 ( V ) は、( y = -1 ) から ( y = 1 ) までの断面の面積を積分することによって求められる：
[
V = \int_{-1}^{1} A(y) \, dy = \int_{-1}^{1} \frac{\sqrt{3}}{4} (1 – y^2)^2 \, dy
]

積分を簡略化する:

被積分関数を展開する：
[
(1 – y^2)^2 = 1 – 2y^2 + y^4
]
したがって、
[
V = \frac{\sqrt{3}}{4} \int_{-1}^{1} (1 – 2y^2 + y^4) \, dy
]

積分を評価する:

積分を個々の項に分割する：
[
V = \frac{\sqrt{3}}{4} \left( \int_{-1}^{1} 1 \, dy – 2 \int_{-1}^{1} y^2 \, dy + \int_{-1}^{1} y^4 \, dy \right)
]
各項を別々に計算する：
[
\int_{-1}^{1} 1 \, dy = 2
]
[
\int_{-1}^{1} y^2 \, dy = \frac{2}{3}
]
[
\int_{-1}^{1} y^4 \, dy = \frac{2}{5}
]
結果を結合する：
[
V = \frac{\sqrt{3}}{4} \left( 2 – 2 \cdot \frac{2}{3} + \frac{2}{5} \right)
]
[
V = \frac{\sqrt{3}}{4} \left( 2 – \frac{4}{3} + \frac{2}{5} \right)
]
[
V = \frac{\sqrt{3}}{4} \left( \frac{30}{15} – \frac{20}{15} + \frac{6}{15} \right)
]
[
V = \frac{\sqrt{3}}{4} \cdot \frac{16}{15}
]
[
V = \frac{4\sqrt{3}}{15}
]

したがって、立体の体積は ( \boxed{\frac{4\sqrt{3}}{15}} ) です。

結果は、GPT-4oのみ正しい解答を出力しました。

GPT-4oとその他2つの計算能力の差は歴然ですが、MiniCPM-Llama3-V 2.5とPhi-3-Visionは問題文を正しく理解できていないようです。

まだまだ総合的な性能についてはGPT-4oには及びません。

テキスト抽出（日本語）

以下の手書きの伝票を読み取らせて、正確にテキストを抽出させてみたいと思います。

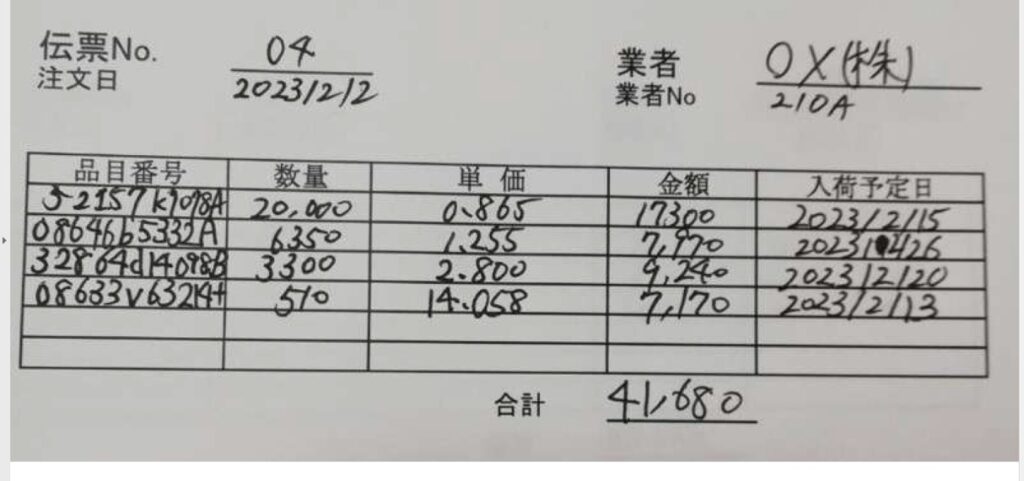
引用元：https://zenn.dev/shungo_a/articles/0f15975c88487f

以下のプロンプトを入力します。

画像内のテキストを抽出して

なお、Phi-3-Visionのみ日本語のプロンプトに対応していないようでしたので、英訳したプロンプトを使用しました。

結果はこのようになりました。

MiniCPM-Llama3-V 2.5の結果はこちら

画像の構成

タイトル

業者No. : 210A
注文日 : 2023/2/12
往票No. : 04

表の内容

品目番号
- 2157k7018A
- 0864665332A
- 32864d14098B
- 08633v6324t
数量
- 20,000
- 1,350
- 3,300
- 570
単価
- 0.865
- 1.255
- 2.800
- 14.058
金額
- 173,000
- 2,725
- 9,240
- 7,170
入荷予定日
- 2023/2/15
- 2023/2/26
- 2023/2/20
- 2023/2/23
合計
- 41,680

Phi-3-Visionの結果はこちら

The text in the image is in Chinese characters. The OCR text provided does not match the content in the image, so I cannot use it to extract text. However, I can provide a translation of the visible text in the image:

企業No. 04
注文日 2023/12/12
業者 OX(株)
業者No 210A
品目證号
數量 20,000
単位 0.865
金額 17300
入購予定日 2023/12/15
086465332A 6.350
単位 1.255
単位 7,170
入購予定日 2023/12/26
32804d14088 3300
単位 2.800
単位 9,240
入購予定日 2023/12/20
08633v63244 570
數量 14.058
単位 7,170
入購予定日 2023/2/13
合計 41/880

The image also contains a handwritten note at the bottom with the number ’41/880′.

GPT-4oの結果はこちら

伝票No.　04
注文日　2023/12/2
業者　OX（株）
業者No.　210A

品目番号　　　　数量　　　　単価　　　　金額　　　　入荷予定日
S-2157 K108A　20,000　　0.865　　 17,300　　2023/12/15
08646 b5337A　 6,350　　 1.255　　 7,970　　 2023/12/26
32864 d14098B　 3,300　　 2.800　　 9,240　　 2023/12/20
08683 v632K4　 570　　 14.058　　 7,170　　 2023/12/13

合計　41,680

結果を比較すると、最も正確にテキストを抽出しているのはGPT-4oで、MiniCPM-Llama3-V 2.5はわずかに間違ったテキストを抽出している箇所が多いです。

GPT-4oとMiniCPM-Llama3-V 2.5は、手書きの読み取りづらいテキストでありながら、日本語の部分もかなり高い精度で抽出しており、高いOCR能力を有していることが分かります。

Phi-3-Visionに関しては、前述の2つのモデルと比較するとその抽出精度はかなり低いと感じました。

今回の検証で、MiniCPM-Llama3-V 2.5はGPT-4oと比較すると総合的な能力ではまだまだ差がありますが、OCR能力に関しては同等の性能を有していることが確認できました。

また、Phi-3-Visionより高い性能を示し、8Bというサイズを考えれば超効率的で高性能なモデルであると言えます。

なお、GPT-4oについて知りたい方はこちらの記事をご覧ください。

WEEL

GPT-4oとは？リアルタイム音声会話ができると話題の最強マルチモーダルLLMを徹底解説 | WEEL WEELメディア事業部AIライターの2scです。みなさん、GPT-4の最新版「GPT-4o」が無料版&有料版ChatGPTに降臨しています！このGPT-4o、なんとこれまでのGPT-4の2倍速で生成…

MiniCPM-Llama3-V 2.5は超高効率のマルチモーダルモデル

MiniCPM-Llama3-V 2.5は、8Bのパラメータを持っており、小型ながらベンチマークではGPT-4VやGemini Proなどの名だたる大規模モデルに匹敵する性能を示しました。

特にOCRBenchでは、GPT-4oより高いスコアを獲得しており、テキストのOCR抽出やテーブルからMarkdownへの変換などのOCR能力が非常に高いことが伺えます。

また、Llama 3をベースにしているため高い言語能力も有しており、日本語を含む30以上の言語に対応しています。

実際に使用したところ、手書きテキスト（日本語を含む）でもGPT-4oと同等程度の非常に高い精度で抽出でき、高いOCR能力を有していることが確認できました。

現在、このモデルをモバイルデバイス上で動作させるための開発が行われており、今後もMiniCPM-Llama3-V 2.5から目が離せません！

生成系AIの業務活用なら！

・生成系AIを活用したPoC開発

・生成系AIのコンサルティング

・システム間API連携

無料ダウンロード

最後に

いかがだったでしょうか？

弊社では

・マーケティングやエンジニアリングなどの専門知識を学習させたAI社員の開発
・要件定義・業務フロー作成を80%自動化できる自律型AIエージェントの開発
・生成AIとRPAを組み合わせた業務自動化ツールの開発
・社内人事業務を99%自動化できるAIツールの開発
・ハルシネーション対策AIツールの開発
・自社専用のAIチャットボットの開発

などの開発実績がございます。

まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。

➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

生成AIを社内で活用していきたい方へ