【GLM‑4.5/GLM‑4.5 Air】高性能と低コストを両立するオープンソースモデルの性能や使い方を徹底解説!

- Z.ai発の最新のフラッグシップ基盤モデル「GLM‑4.5」とその軽量版「GLM‑4.5 Air」が同時リリース
- 推論・コーディング・エージェント運用の3つの強みを統合したモデル
- Apache 2.0ライセンスでリリースされ、商用利用や再配布なども可能
2025年7月28日、Z.ai(旧 Zhipu)は最新のフラッグシップ基盤モデル「GLM‑4.5」とその軽量版「GLM‑4.5 Air」を同時リリースしました!
両モデルは、独自開発のMixture‑of‑Experts(MoE)アーキテクチャを採用しており、推論・コーディング・エージェント運用の3つの強みを統合したモデルとなっています。
総パラメータ数3,550億のGLM‑4.5は、OpenAIやAnthropicの上位モデルと同水準の性能を誇っており、総パラメータ数1,060億のGLM‑4.5 Airは、コスト効率を極限まで高めつつ、上位モデルと遜色ない推論力を発揮するそうです。
本記事では、GLM‑4.5とGLM‑4.5 Airの性能やそれぞれの違い、使い方まで徹底解説します。
ぜひ最後までご覧ください!
\生成AIを活用して業務プロセスを自動化/
GLM-4.5とGLM-4.5 Airの概要

基盤モデルであるGLM‑4.5は、総パラメータ数3,550億・アクティブ320億で、128kトークンの長大コンテキストとハイブリッド推論モード(thinking/non‑thinking)を標準搭載しています。
thinkingモードでは、複雑な数理推論や外部ツール呼び出しを前提にした「深く考える」動作を行い、non‑thinkingモードでは、チャットなどの即応性が求められるシーンで高速な応答を返します。
一方の軽量版であるGLM‑4.5 Airは、同じ設計思想を保ちつつ、総パラメータを1,060億・アクティブ120億に抑えたライトモデルです。それでも、TAU‑BenchやMMLU Proといった総合ベンチマークで上位のスコアを記録しており、推論能力とコストパフォーマンスのバランスが良いです。
両モデルともに、学習に15兆トークンが投入されており、コーディング・推論・エージェント特化データで追加のファインチューニングがなされています。
こういった背景から、コード生成からWebブラウジング付きタスク、関数呼び出し自動化まで、多彩なケースを一気通貫でこなす万能型LLMとなっています。
なお、AIエージェントを活用した業務自動化について、詳しく知りたい方は以下の記事を参考にしてみてください。

GLM-4.5とGLM-4.5 Airの性能
公式のベンチマークでは、GLM‑4.5が12種類の代表的な指標(MMLU Pro・SWE‑bench Verified・BrowseComp など)で平均63.2点を記録し、オープン/クローズドソース混在の世界ランキングで3位、オープンソースでは1位を獲得しています。
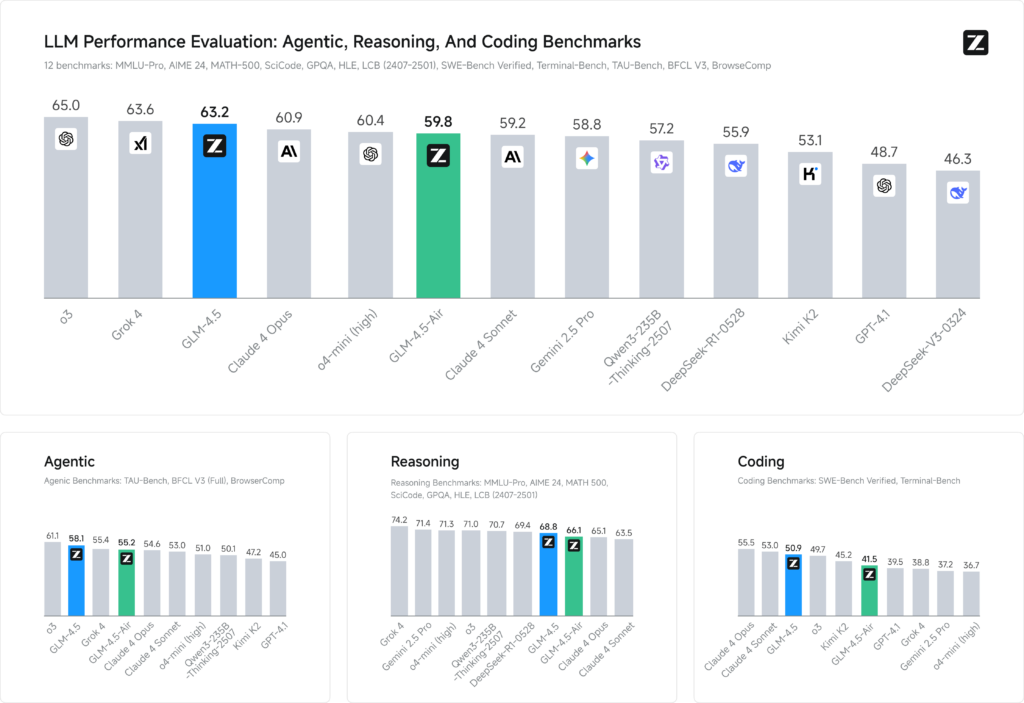
GLM‑4.5 Airも平均59.8点で6位につけており、パラメータ効率では両モデルがパレートフロンティアを形成していると言えますね。
BrowseCompでは、GLM-4.5はClaude 4 Opusの18.8%を超えた26.4%の正答率を達成しています。また、SWE‑bench Verifiedでも64.2%、Airは57.6%とGPT‑4.1を上回る実力を見せています。
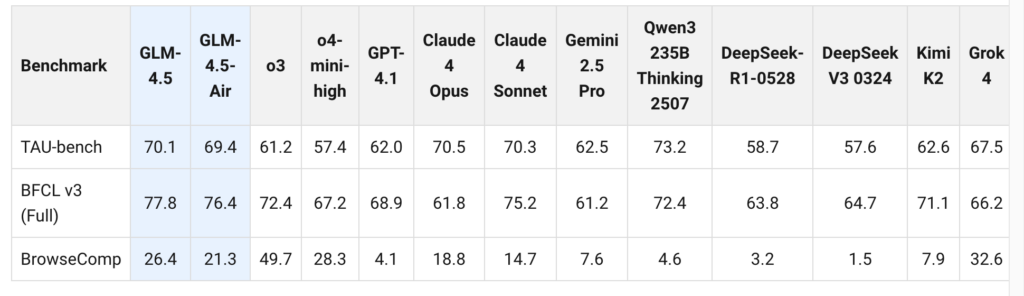

さらに、1秒あたり100トークン超の生成速度や128kコンテキスト対応によって、長文要約やマルチファイルコード編集においても高速に処理してくれることが想定できます。
GLM-4.5とGLM-4.5 Airのライセンス
GLM‑4.5シリーズは、Apache 2.0ライセンスとして公開され、MITと表記された派生モデルカードも存在しています。いずれも寛容なパーミッシブライセンスで、商用利用や再配布を含むほぼすべての用途が許可されています。
| 利用用途 | gpt-oss-120b | gpt-oss-20b |
|---|---|---|
| 商用利用 | ⭕️ | |
| 改変 | ⭕️ | |
| 配布 | ⭕️ | |
| 特許使用 | ⭕️ | |
| 私的使用 | ⭕️ |
ライブラリ依存もオープンなため、独自コンパイルや量子化モデルの再配布もライセンス上問題ないと考えられます。
ただし、ライセンスは変更となる可能性がありますので、商用利用等する際には、最新情報を確認するようにしましょう。
GLM-4.5とGLM-4.5 Airの料金プラン
Z.aiの公式APIは、入力100万トークンあたり0.8円、出力2円で提供されています。また、グローバル向けには OpenRouter経由で米ドル建て価格も公表されていて、GLM‑4.5が0.60ドル/2.20ドル、GLM‑4.5 Airが0.20ドル/1.10ドル(入力/出力各100万トークン)となっています。
Claude 4 SonnetやGPT‑4oと比べると、だいたい5〜10分の1のコストで、同等クラスの推論力を得られる計算になりますね。個人であれば、無料クレジット付きのChatポータルで試すこともできるので、導入ハードルが低いのがうれしいポイントです。
| プラン | 入力単価(100万トークン) | 出力単価(100万トークン) |
|---|---|---|
| GLM‑4.5(API RMB) | 0.8円 | 2.0円 |
| GLM‑4.5(API USD) | 0.6ドル | 2.20ドル |
| GLM‑4.5 Air(API USD) | 0.2ドル | 1.10ドル |
参考:https://openrouter.ai/z-ai/glm-4.5
GLM-4.5とGLM-4.5 Airの使い方
「GLM‑4.5」と「GLM‑4.5 Air」はチャットUIでの利用とAPIでの利用の2通りの使い方があります。
チャットUIの使い方
まずはZ.aiのポータルサイトchat.z.aiにアクセスし、画面右上の「Sign in」からアカウントを作成しましょう。
ログインが完了すると、チャットを利用できる状態になります。以下の画像のように、左側のモデル一覧に「GLM‑4.5」と「GLM‑4.5 Air」が並んでいるのが確認できます。
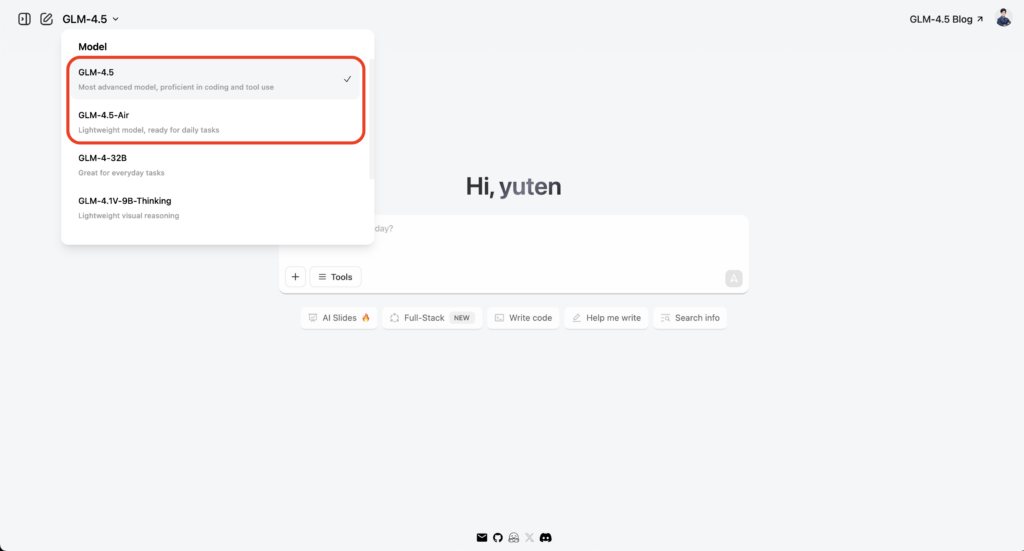
チャットUI版では、ハイブリッド推論モード(thinking/non‑thinking)は明示的に指定できないみたいですね。
APIでの使い方
ご自身のアプリだったりスクリプトに統合したい場合は、OpenAI互換のREST APIを活用すると便利です。Pythonベースでの最小構成の例をご紹介します。
OpenRouter経由でのAPIキー作成手順は以下の通りです。
APIダッシュボードにアクセスしてログインし、Create API Keyボタンを押す。
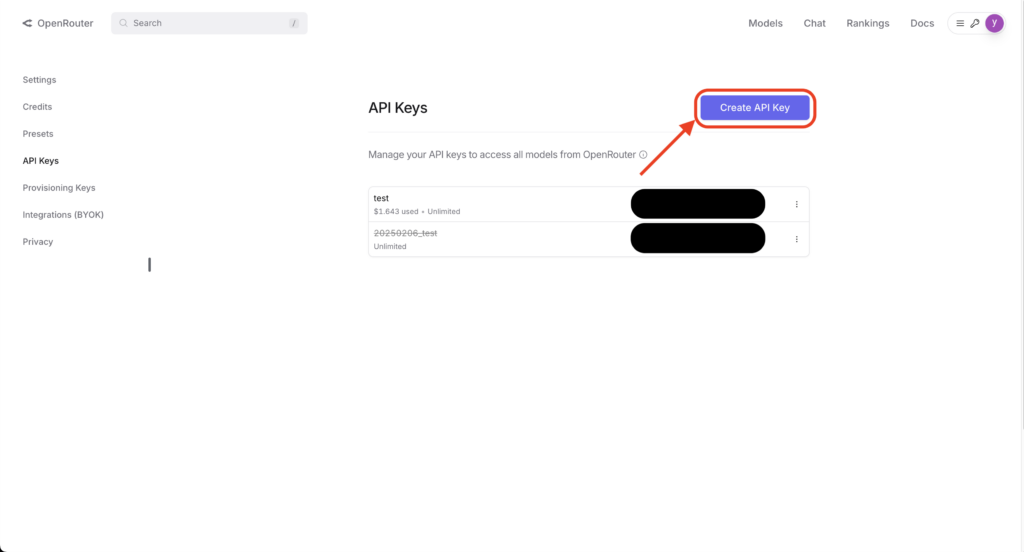
キーの名前を入力して、Createボタンを押下。
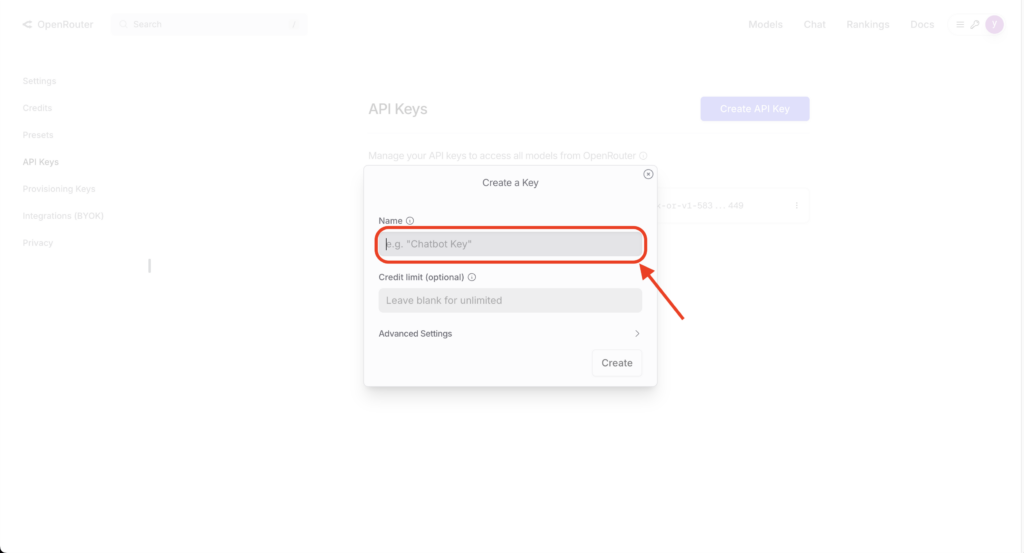
作成されたAPIキーをコピーして、安全な場所に保管。
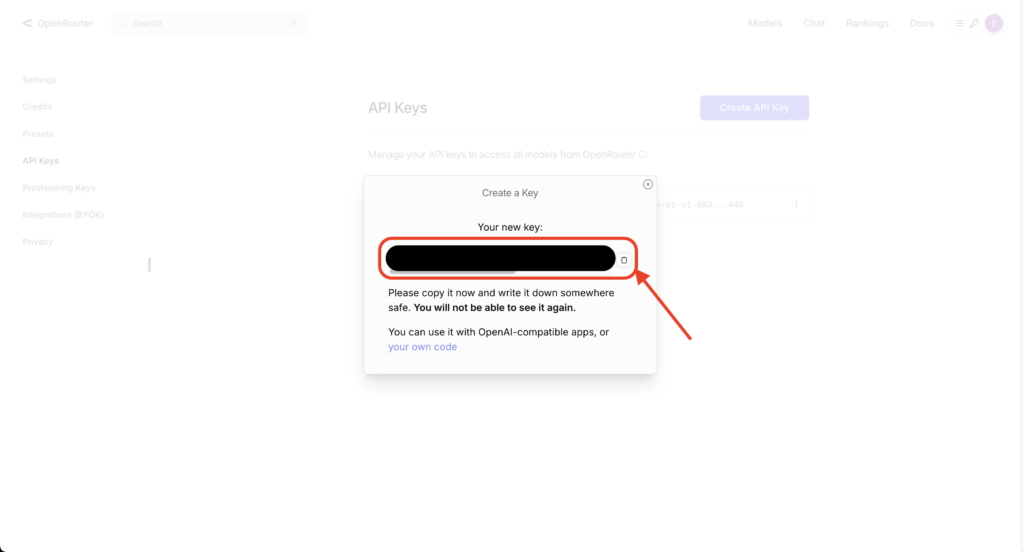
以上でAPIキーの取得は完了です。あとは以下の例のようにPythonコードを実行することで、GLM-4.5シリーズを利用することができます。
# 必要ライブラリをインストール
%pip install -q --upgrade openai
# API キーを安全に入力して環境変数にセット
import os, getpass
# OpenRouter のダッシュボードで発行したキーを入力(例: sk-xxxxxxxx)
os.environ["OPENAI_API_KEY"] = getpass.getpass("Enter your OpenRouter API key: ")
from openai import OpenAI
client = OpenAI(base_url="https://openrouter.ai/api/v1")
resp = client.chat.completions.create(
model="z-ai/glm-4.5-air",
messages=[{"role": "user", "content": "自己紹介して"}],
stream=False,
extra_body={
# 好みでどちらか一方を指定
"reasoning": {"enabled": True}
# "thinking": {"type": "enabled"}
}
)
print(resp.choices[0].message.content)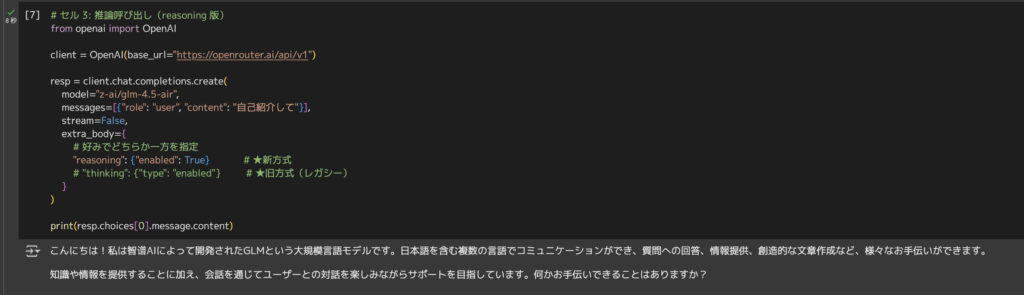
API経由でも問題なく動作確認できました。
今回は「自己紹介して」というプロンプトに対して、「こんにちは!私は智谱AIによって開発されたGLMという大規模言語モデルです。日本語を含む複数の言語でコミュニケーションができ、質問への回答、情報提供、創造的な文章作成など、様々なお手伝いができます。 知識や情報を提供することに加え、会話を通じてユーザーとの対話を楽しみながらサポートを目指しています。何かお手伝いできることはありますか?」と返答してくれました。
GLM-4.5とOpenAI o3の比較検証してみた
12種類の代表的な指標(MMLU Pro・SWE‑bench Verified・BrowseComp など)で平均63.2点を記録したGLM‑4.5と、65点を獲得したOpenAI o3モデルを比較して、GLM-4.5の結果がo3に対して遜色ないレベルなのかどうか検証していきます。
両モデルともにチャットUIで実行していきます。
数理タスク
まずは、数理タスクとして、確率の条件付き推論を試していきます。
プロンプトはこちら
赤玉3 白玉5 黒玉2 の箱から玉を1個引いて戻さずにもう1個引く。少なくとも1個が赤である確率を計算し説明してくださいo3の出力結果はこちら
考え方
「少なくとも 1 個が赤」という事象の確率は、
𝑃
(
少なくとも1赤
)
=
1
−
𝑃
(
赤が1 個も出ない
)
P(少なくとも1赤)=1−P(赤が1 個も出ない)
と補集合で求めるとラクです。
1. 事前情報
箱の中 = 10 個(赤 3、白 5、黒 2)
戻さずに 2 個を連続で引く(無作為・同確率)
2. 「赤が 1 個も出ない」確率
赤以外(白・黒)は 7 個あります。
手順 残っている玉 非赤の玉数 非赤を引く確率
1回目 10 個 7 個
7
10
10
7
2回目 9 個 6 個
6
9
=
2
3
9
6
=
3
2
したがって
𝑃
(
赤が0個
)
=
7
10
×
6
9
=
42
90
=
7
15
P(赤が0個)=
10
7
×
9
6
=
90
42
=
15
7
3. 補集合で求める
𝑃
(
少なくとも1赤
)
=
1
−
7
15
=
8
15
P(少なくとも1赤)=1−
15
7
=
15
8
4. 結論
玉を 2 個続けて引いたときに**少なくとも 1 個が赤玉である確率は
8
15
15
8
(約 53.3 %)**です。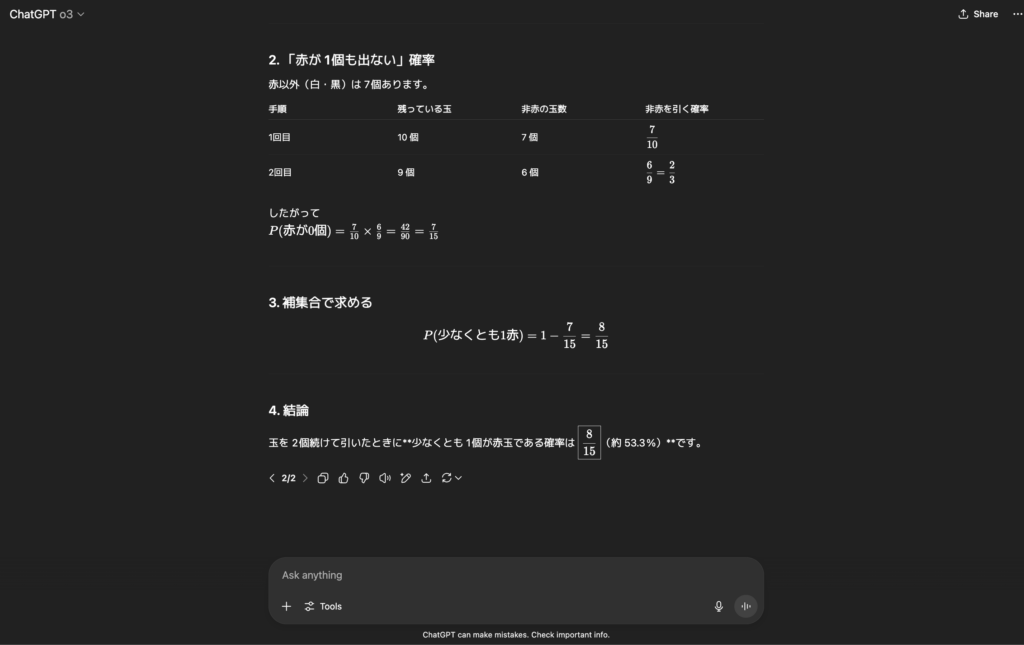
GLM-4.5の出力結果はこちら
問題の理解
箱には赤玉3個、白玉5個、黒玉2個の合計10個の玉があります。玉を1個引いて戻さず(非復元抽出)、もう1個引くとき、「少なくとも1個が赤である」確率を求めます。
解法の選択
「少なくとも1個が赤である」という事象は、以下の3つの場合を含みます:
最初の玉が赤で、2番目の玉が赤でない
最初の玉が赤でなく、2番目の玉が赤
両方の玉が赤
直接これらの確率を計算して足し合わせることもできますが、余事象(「1個も赤でない」確率)を求めて、全体の確率(1)から引く方法が簡単です。ここでは、余事象を用いた方法で計算します。
余事象の計算
「1個も赤でない」とは、引いた2個の玉が両方とも赤でない(白または黒)ことです。赤でない玉は白5個 + 黒2個 = 7個です。
玉を戻さずに2回引くので、順序を考慮した確率を計算します。
最初に赤でない玉を引く確率:赤でない玉は7個あるので、
10
7
最初に赤でない玉を引いた後、残りの玉は9個(赤でない玉は6個)なので、2番目に赤でない玉を引く確率:
9
6
=
3
2
したがって、両方とも赤でない確率(余事象の確率)は:
10
7
×
9
6
=
10
7
×
3
2
=
30
14
=
15
7
求める確率の計算
全体の確率は1なので、「少なくとも1個が赤である」確率は:
1−
15
7
=
15
15
−
15
7
=
15
8
直接計算による確認
直接計算でも同じ結果が得られることを確認します。順序を考慮した場合の数で計算します。
全体の可能な結果:最初に10個の玉から1個選び、次に9個の玉から1個選ぶので、10×9=90 通り。
少なくとも1個赤の場合の数:
最初が赤で2番目が赤でない:赤玉3個から1個選び(3通り)、次に赤でない玉7個から1個選ぶ(7通り)→ 3×7=21 通り
最初が赤でなく2番目が赤:赤でない玉7個から1個選び(7通り)、次に赤玉3個から1個選ぶ(3通り)→ 7×3=21 通り
両方とも赤:赤玉3個から1個選び(3通り)、次に残りの赤玉2個から1個選ぶ(2通り)→ 3×2=6 通り
合計:21+21+6=48 通り
したがって、確率は:
90
48
=
90÷6
48÷6
=
15
8
組み合わせによる確認
順序を考慮しない組み合わせでも計算できます。
全体の選び方:10個から2個選ぶ組み合わせ (
2
10
)=
2×1
10×9
=45 通り。
1個も赤でない選び方:赤でない玉7個から2個選ぶ組み合わせ (
2
7
)=
2×1
7×6
=21 通り。
少なくとも1個赤の選び方:45−21=24 通り。
したがって、確率は:
45
24
=
45÷3
24÷3
=
15
8
結論
いずれの方法でも同じ結果が得られます。「少なくとも1個が赤である」確率は
15
8
です。
最終回答
15
8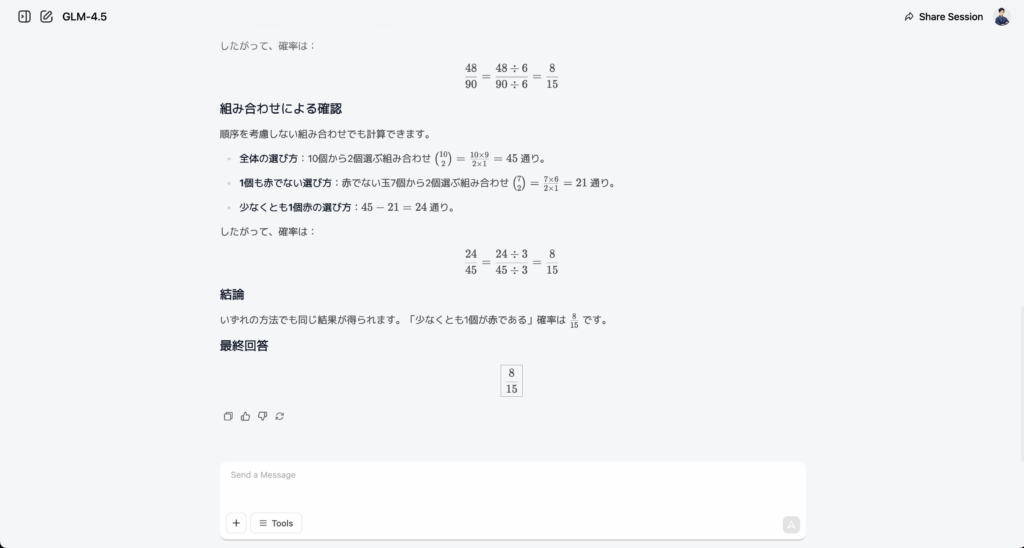
結果はどちらも正解でした。推論内容についてもどちらも充分な思考がされていますね。
ただ、出力までに要した時間はo3が約7秒ほどだったのに対して、GLM-4.5は約2分ほどでした。GLM-4.5は、深い推論処理を行うため、多段階思考タスクでは処理時間が長くなる傾向があるようです。
コーディングタスク
続いてコーディングタスクを試してみます。
プロンプトはこちら
関数 coin_change(amount:int, coins:list[int])->list[int] を実装し、最小枚数で金額を作る硬貨枚数リストを返してください。
要件
- 戻り値の list 長さは len(coins)。各 index に使用枚数
- 解が複数ある場合は辞書順で最小の組み合わせ
- 解なし(作れない)なら空リスト []
入出力例
amount=11, coins=[1,5,6,9] → [1,0,0,1] # 1×1 + 9×1
amount=3, coins=[2,4] → [] # 作れない
合格基準
- timeit で amount=10⁴, |coins|≤100 を 0.2 sec 以内
- 再帰ではなく自作 DP を用いるo3の出力結果はこちら
# coin_change.py
from collections import deque
from typing import List
def coin_change(amount: int, coins: List[int]) -> List[int]:
"""
最小枚数で金額を作る硬貨構成を BFS で求める.
───────────────────────────────────────────────
• BFS のレイヤー = 使用枚数 → 最小枚数を保証
• コインを常に昇順で展開 → 同枚数内で辞書順最小を保証
計算量 O(amount * len(coins))、メモリ O(amount)
"""
n = len(coins)
# visited[a] = a を作るのに最後に使ったコイン index(未訪問は -1)
visited = [-1] * (amount + 1)
prev = [-1] * (amount + 1) # 一つ前の金額
q = deque([0])
visited[0] = -2 # 0 は起点として特別扱い
while q:
cur = q.popleft()
if cur == amount: # 目標金額に到達
break
for i, c in enumerate(coins): # 昇順で展開 = 辞書順優先
nxt = cur + c
if nxt > amount or visited[nxt] != -1:
continue
visited[nxt] = i # この金額は初到達
prev[nxt] = cur
q.append(nxt)
if visited[amount] == -1: # 解なし
return []
# ── 逆ポインタをたどって枚数を数える ─────────────────
counts = [0] * n
x = amount
while x != 0:
idx = visited[x]
counts[idx] += 1
x = prev[x]
return counts# test.py
import unittest, timeit
from coin_change_o3 import coin_change
class TestCoinChange(unittest.TestCase):
# 公式サンプル(期待値を修正)
def test_given_examples(self):
self.assertEqual(coin_change(11, [1, 5, 6, 9]), [0, 1, 1, 0])
self.assertEqual(coin_change(3, [2, 4]), [])
# 同枚数で辞書順判定が効く例
def test_lexicographic(self):
# 4 を 2×2 が最小枚数(2 枚): [0,2] が正
self.assertEqual(coin_change(4, [1, 2]), [0, 2])
# 作れない例
def test_impossible(self):
self.assertEqual(coin_change(7, [2, 4]), [])
# パフォーマンス (amount=1e4, |coins|=100)
def test_time_limit(self):
amount = 10_000
coins = list(range(1, 101))
t = timeit.timeit(
stmt='coin_change(amount, coins)',
globals={'coin_change': coin_change,
'amount': amount,
'coins': coins},
number=1
)
self.assertLessEqual(
t, 0.20,
msg=f"Performance too slow: {t:.3f} sec (limit 0.20 sec)"
)
if __name__ == "__main__":
unittest.main(verbosity=2)o3の出力結果をそのまま反映したpyファイルの実行結果
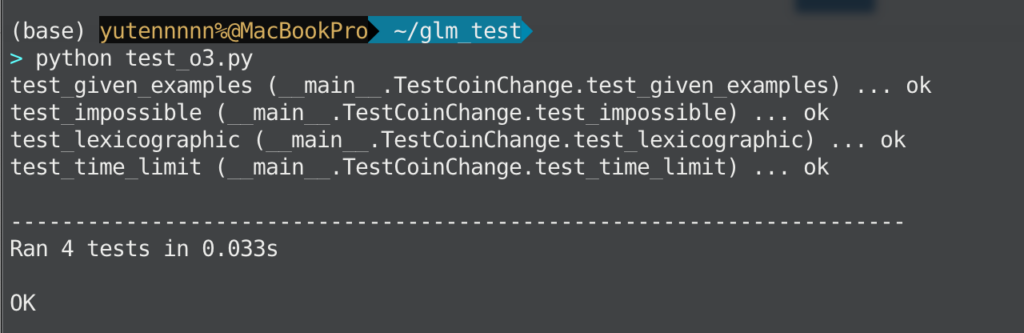
今回はo3の実行時間が約30秒ほど、GLM-4.5は数分の思考の上で途中で思考が止まってしまい、実行結果は出力されませんでした。(5回ほど実行し直したりしましたがダメで、その間に先ほどの数理タスクも実行してみましたが、そちらは問題なく実行できたので、特定のタスクにおいては、コンテキスト?なのか何か他の原因なのか?で、実行が止まってしまうことがあるのかもしれません。)
また、API版だと実行がうまくいく可能性もありますので、気になる方でコストが許容できる方はぜひ試してみてください。
以上、今回の検証結果としては、「数理タスクにおいては実行時間の違いはあれどo3と遜色ない結果の出力ができる」、「特定のタスクにおいては、実行が完了しないケースがある」という結果になりました。
気になる方は、他のタスクでもぜひ試してみてください!
なお、OpenAI o3について詳しく知りたい方は、以下の記事も参考にしてみてください。
まとめ
GLM‑4.5シリーズは、性能の高さとコストの低さを兼ね備えており、商用利用や学術研究にも使えるモデルファミリーとして登場しました。
3,550億パラメータの基盤モデルはOpenAI o3やGrok 4に迫る性能で、ライト版のAirでも実用ベンチマークにおいて上位を記録しています。
また、Apache 2.0ベースのライセンス、100万トークンあたり十数円から数百円という価格の低さは、小規模チーム個人開発者にとっても大きな魅力です。
コード生成やエージェント構築の現場でも活用する選択肢に入ってくると思いますので、気になる方はぜひ試してみてください!

最後に
いかがだったでしょうか?
推論、コーディング、エージェント運用まで一気通貫で対応可能。個人開発・クリエイティブ用途までGLM-4.5は最適なツールです。
株式会社WEELは、自社・業務特化の効果が出るAIプロダクト開発が強みです!
開発実績として、
・新規事業室での「リサーチ」「分析」「事業計画検討」を70%自動化するAIエージェント
・社内お問い合わせの1次回答を自動化するRAG型のチャットボット
・過去事例や最新情報を加味して、10秒で記事のたたき台を作成できるAIプロダクト
・お客様からのメール対応の工数を80%削減したAIメール
・サーバーやAI PCを活用したオンプレでの生成AI活用
・生徒の感情や学習状況を踏まえ、勉強をアシストするAIアシスタント
などの開発実績がございます。
生成AIを活用したプロダクト開発の支援内容は、以下のページでも詳しくご覧いただけます。
➡︎株式会社WEELのサービスを詳しく見る。
まずは、「無料相談」にてご相談を承っておりますので、ご興味がある方はぜひご連絡ください。
➡︎生成AIを使った業務効率化、生成AIツールの開発について相談をしてみる。

「生成AIを社内で活用したい」「生成AIの事業をやっていきたい」という方に向けて、生成AI社内セミナー・勉強会をさせていただいております。
セミナー内容や料金については、ご相談ください。
また、サービス紹介資料もご用意しておりますので、併せてご確認ください。





